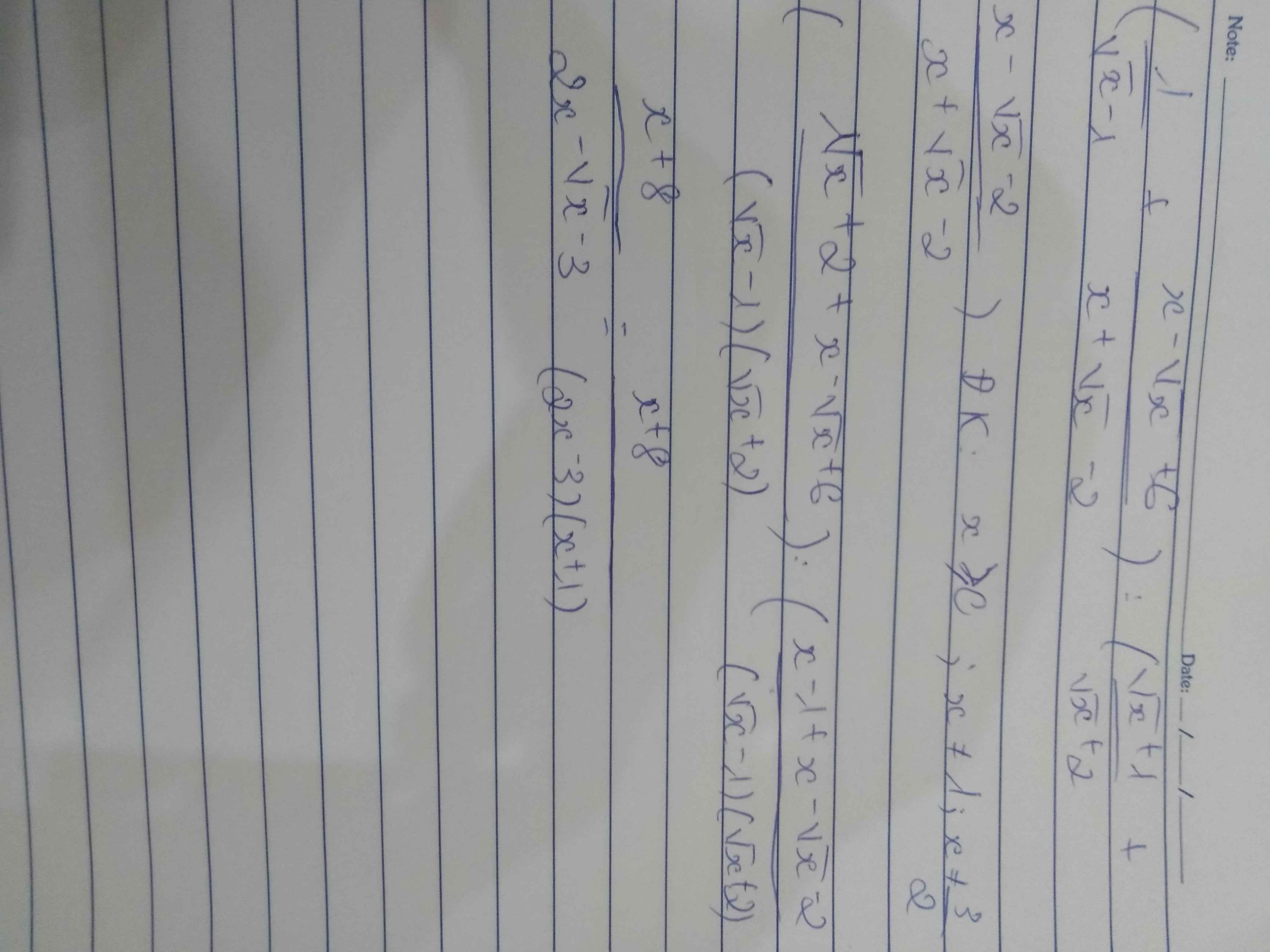\(N=\dfrac{x+\sqrt{x}+2}{x+\sqrt{x}}-\dfrac{\sqrt{x}-1}{x+1}\) (ĐK: \(x>0\))

\(N=\dfrac{x+\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-1}{x+1}\)

\(N=\dfrac{\left(x+\sqrt{x}+2\right)\left(x+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}\)

\(N=\dfrac{x^2+x+x\sqrt{x}+\sqrt{x}+2x+2}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}-\dfrac{x\sqrt{x}-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}\)

\(N=\dfrac{x^2+3x+x\sqrt{x}+\sqrt{x}+2-x\sqrt{x}+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}\)

\(N=\dfrac{x^2+3x+2\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}+1\right)\left(x+1\right)}\)

Câu 1:

Sửa đề: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)

Ta có: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)

\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{1}{\sqrt{x}+3}\right):\left(\dfrac{x+3\sqrt{x}-2\left(\sqrt{x}+3\right)+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}:\dfrac{x+3\sqrt{x}-2\sqrt{x}-6+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x+\sqrt{x}}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=1\)

Câu 3: 

Ta có: \(Q=\left(\dfrac{a}{a-2\sqrt{a}}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{a-4\sqrt{a}+4}\)

\(=\left(\dfrac{a}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-2\right)^2}\)

\(=\dfrac{a+\sqrt{a}}{\sqrt{a}-2}\cdot\dfrac{\sqrt{a}-2}{\sqrt{a}+1}\cdot\dfrac{\sqrt{a}-2}{1}\)

\(=\sqrt{a}\left(\sqrt{a}-2\right)\)

\(=a-2\sqrt{a}\)

Với `x >= 0,x ne 4` có:

`M=[(\sqrt{x}+1)(\sqrt{x}+2)+2\sqrt{x}(\sqrt{x}-2)-2-5\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]`

`M=[x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]`

`M=[3x-6\sqrt{x}]/[(\sqrt{x}-2)(\sqrt{x}+2)]=[3\sqrt{x}]/[\sqrt{x}+2]`

____________

`N=(1/[\sqrt{a}-1]-1/\sqrt{a}):([\sqrt{a}+1]/[\sqrt{a}-2]-[\sqrt{a}+2]/[\sqrt{a}-1])`

      - Biểu thức `N` là như vầy?

Với `a > 0,a ne 1,a ne 4` có:

`N=[\sqrt{a}-\sqrt{a}+1]/[\sqrt{a}(\sqrt{a}-1)]:[(\sqrt{a}+1)(\sqrt{a}-1)-(\sqrt{a}+2)(\sqrt{a}-2)]/[(\sqrt{a}-2)(\sqrt{a}-1)]`

`N=1/[\sqrt{a}(\sqrt{a}-1)].[(\sqrt{a}-2)(\sqrt{a}-1)]/[a-1-a+4]`

`N=[\sqrt{a}-2]/[3\sqrt{a}]`

Với \(x\ge0;x\ne4\)

Khi đó:

\(M=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}{x-4}+\dfrac{2\sqrt{x}\left(\sqrt{x}-2\right)}{x-4}-\dfrac{2+5\sqrt{x}}{x-4}\\ =\dfrac{x+2\sqrt{x}+\sqrt{x}+2}{x-4}+\dfrac{2x-4\sqrt{x}}{x-4}-\dfrac{2+5\sqrt{x}}{x-4}\\ =\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{x-4}\\ =\dfrac{3x-6\sqrt{x}}{x-4}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)

Với \(a>0;a\ne1;a\ne4\) 

Khi đó:

\(N=(\dfrac{\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}-\dfrac{\sqrt{a}-1}{\sqrt{a}\left(\sqrt{a}-1\right)}):\left(\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\\ =\left(\dfrac{\sqrt{a}}{a-\sqrt{a}}-\dfrac{\sqrt{a}-1}{a-\sqrt{a}}\right):\left(\dfrac{a-1}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}-\dfrac{a-4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\\ =\dfrac{1}{a-\sqrt{a}}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\\ =\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{3}\\ =\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}{\sqrt{a}\left(\sqrt{a}-1\right).3}\\ =\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)

mình nghĩ đề nên là \(N=\left(\dfrac{3}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}-6}{x-2\sqrt{x}}+\dfrac{1}{\sqrt{x}}\right)\) chớ như bạn rút gọn không hết

\(N=\left(\dfrac{3}{\sqrt{x}+2}-\dfrac{1}{\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}-6}{x-2\sqrt{x}}+\dfrac{1}{\sqrt{x}}\right)\left(x>0,x\ne2\right)\)

\(=\dfrac{3\left(\sqrt{x}-2\right)-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\left(\dfrac{\sqrt{x}-6}{\sqrt{x}\left(\sqrt{x}-2\right)}+\dfrac{1}{\sqrt{x}}\right)\)

\(=\dfrac{2\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{\sqrt{x}-6+\sqrt{x}-2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{2\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}:\dfrac{2\sqrt{x}-8}{\sqrt{x}\left(\sqrt{x}-2\right)}\)

\(=\dfrac{2\sqrt{x}-8}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{2\sqrt{x}-8}=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

\(a,C=\dfrac{2x^2-x-x-1+2-x^2}{x-1}\left(x\ne1\right)\\ C=\dfrac{x^2-2x+1}{x-1}=\dfrac{\left(x-1\right)^2}{x-1}=x-1\\ b,D=\dfrac{1+\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}\left(a>0;a\ne1\right)\\ D=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)

Có 

Điều kiện: \(x\ge1\)

\(A=\sqrt{x-2\sqrt{x-1}}+\sqrt{x+2\sqrt{x-1}}\\ A=\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}\\ A=\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}\\ A=\left|\sqrt{x-1}-1\right|+\sqrt{x-1}+1\)

\(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\)

\(=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)

\(=\sqrt{\left(\sqrt{x-1}\right)^2+2\cdot\sqrt{x-1}\cdot1+1^2}+\sqrt{\left(\sqrt{x-1}\right)^2-2\sqrt{x-1}\cdot1+1^2}\)

\(=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)

\(=\left|\sqrt{x-1}+1\right|+\left|\sqrt{x-1}-1\right|\)

\(=\sqrt{x-1}+1+\sqrt{x-1}-1\)

\(=2\sqrt{x-1}\)

\(=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)

\(=\left|\sqrt{x-1}+1\right|+\left|\sqrt{x-1}-1\right|\)

\(=\sqrt{x-1}+1+\sqrt{x-1}-1=2\sqrt{x-1}\)

a. \(N=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right).\dfrac{4\sqrt{x}}{3}\)  \(\left(ĐKXĐ:x\ge0\right)\)

\(N=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{x-\sqrt{x}+1}{x\sqrt{x}+1}\right).\dfrac{4\sqrt{x}}{3}\)

\(\text{​​}\text{​​}N=\dfrac{\sqrt{x}+1}{x\sqrt{x}+1}.\dfrac{4\sqrt{x}}{3}\)

\(N=\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)

b.\(N=\dfrac{8}{9}\Leftrightarrow\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}=\dfrac{8}{9}\)

\(\Leftrightarrow3\sqrt{x}=2x-2\sqrt{x}+2\)

\(\Leftrightarrow\left(2\sqrt{x}-1\right)\left(\sqrt{x}-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{4}\\x=4\end{matrix}\right.\)

c.\(\dfrac{1}{N}>\dfrac{3\sqrt{x}}{4}\Leftrightarrow\dfrac{3\left(x-\sqrt{x}+1\right)}{4\sqrt{x}}>\dfrac{3\sqrt{x}}{4}\)

\(\Leftrightarrow x-\sqrt{x}+1>x\)

\(\Leftrightarrow x< 1\)

a: ĐKXĐ: \(x\ge0\)

Ta có: \(N=\left(\dfrac{x+2}{x\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\right)\cdot\dfrac{4\sqrt{x}}{3}\)

\(=\dfrac{x+2-x+\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\cdot\dfrac{4\sqrt{x}}{3}\)

\(=\dfrac{4\sqrt{x}}{3x-3\sqrt{x}+3}\)

\(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{x-\sqrt{x}+6}{x+\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{x-\sqrt{x}-2}{x+\sqrt{x}-2}\right)\left(x\ge0,x\ne1\right)\)

\(=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{x-\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\right)\)

\(=\dfrac{\sqrt{x}+2+x-\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+x-\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+8}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}:\dfrac{2x-\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}\)

\(=\dfrac{x+8}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{2x-\sqrt{x}-3}=\dfrac{x+8}{2x-\sqrt{x}-3}\)

Ta có: \(\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{x-\sqrt{x}+6}{x+\sqrt{x}-2}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{x-\sqrt{x}-2}{x+\sqrt{x}-2}\right)\)

\(=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{x-\sqrt{x}+6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\right)\)

\(=\dfrac{\sqrt{x}+2+x-\sqrt{x}+6}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}:\dfrac{x-1+x-\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)

\(=\dfrac{x+8}{2x-\sqrt{x}-3}\)