pt bậc 2 hàm số lượng giác
2cosx - 5sinx/2 - 2 = 0
số nghiệm của pt (5sinx-4) cosx=0 trên đoạn [ -2π,3π]
\(\Leftrightarrow\left[{}\begin{matrix}cosx=0\\sinx=\frac{4}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k\pi\\x=arcsin\left(\frac{4}{5}\right)+m2\pi\\x=\pi-arcsin\left(\frac{4}{5}\right)+n2\pi\end{matrix}\right.\)
Do \(-2\pi\le x\le3\pi\)
\(\Rightarrow\left\{{}\begin{matrix}-2\pi\le\frac{\pi}{2}+k\pi\le3\pi\\-2\pi\le arcsin\left(\frac{4}{5}\right)+m2\pi\le3\pi\\-2\pi\le\pi-arcsin\left(\frac{4}{5}\right)+n2\pi\le3\pi\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\frac{5}{2}\le k\le\frac{5}{2}̸\\-1,15< m< 1,35\\-1,35< n< 1,14\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}k=\left\{-2;-1;0;1;2\right\}\\m=\left\{-1;0;1\right\}\\n=\left\{-1;0;1\right\}\end{matrix}\right.\)
Có 11 nghiệm
Cho hàm số f(x) thỏa mãn f ' x = 2 − 5 sin x và f(0)=10. Mệnh đề nào dưới đây đúng?
A. f x = 2 x + 5 cos x + 5
B. f x = 2 x + 5 cos x + 3
C. f x = 2 x − 5 cos x + 10
D. f x = 2 x − 5 cos x + 15
2:Khi nào hệ pt có nghiệm duy nhất?Vô nghiệm?Vô số nghiệm?
(mỗi trường hợp cho 1 VD)
3:Lấy 3 vd về hàm số bậc nhất?Lấy 3 vd về hàm số bậc 2?
4:Viết công thức nghiệm giải pt bậc 2
5:Nếu các bước giải bài toán = cách lập pt hoặc hệ pt
6:Phát biểu định lý Vi-ét và cách nhẩm nghiệm
7:Nêu định nghĩa,tính chất,dấu hiệu nhận biết về tứ giác nội tiếp
8:Nêu cách chứng minh đẳng thức tích
9:Nêu cách chứng minh tứ giác nội tiếp
9:Chứng minh cho bốn đỉnh của tứ giác cách đều một điểm nào đó
Chứng minh tứ giác có tổng 2 góc đối bằng 180°
Chứng minh từ hai đỉnh cùng kề một cạnh cùng nhìn một cạnh dưới hai góc bằng nhau. Nếu một tứ giác có tổng số đo hai góc đối bằng thì tứ giác đó nội tiếp được trong một đường tròn.
7:dấu hiệu :Tứ giác có tổng hai góc đối bằng 180∘ . - Tứ giác có góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó. - Tứ giác có bốn đỉnh cách đều một điểm (mà có thể xác định được). Điểm đó là tâm đường tròn ngoại tiếp tứ giác.
định nghĩa: Trong Hình học phẳng, một tứ giác nội tiếp là một tứ giác mà cả bốn đỉnh đều nằm trên một đường tròn. Đường tròn này được gọi là đường tròn ngoại tiếp, và các đỉnh của tứ giác được gọi là đồng viên. Tâm và bán kính đường tròn lần lượt được gọi là tâm đường tròn ngoại tiếp và bán kính đường tròn ngoại tiếp.
tính chất: Trong tứ giác nội tiếp, cặp hai tam giác đối nhau qua giao hai đường chéo đồng dạng với nhau. trong đó E và F lần lượt là giao điểm hai cặp cạnh đối của tứ giác. Với một bộ bốn cạnh là bốn cạnh một tứ giác nội tiếp, có thể thay đổi thứ tự các cạnh theo một trật tự bất kỳ
6: viet thuận:
Cho phương trình bậc 2 một ẩn: ax2+bx+c=0 (a≠0) (*) có 2 nghiệm x1 và x2. Khi đó 2 nghiệm này thỏa mãn hệ thức sau:
Hệ quả: Dựa vào hệ thức Viet khi phương trình bậc 2 một ẩn có nghiệm, ta có thể nhẩm trực tiếp nghiệm của phương trình trong một số trường hợp đặc biệt:
Nếu a+b+c=0 thì (*) có 1 nghiệm x1=1 và x2=c/aNếu a-b+c=0 thì (*) có nghiệm x1=-1 và x2=-c/aviet đảoGiả sử hai số thực x1 và x2 thỏa mãn hệ thức:
phép nhẩm: “Phân tích hệ số ![]() thành tích và
thành tích và ![]() thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số
thành tổng”. Trong hai phép nhẩm đó, bạn nên nhẩm hệ số ![]() trước rồi kết hợp với
trước rồi kết hợp với ![]() để tìm ra hai số thỏa mãn tích bằng
để tìm ra hai số thỏa mãn tích bằng ![]() và tổng bằng
và tổng bằng ![]() .
.
Cho pt bậc 2 x^2+5x+3m=0 (m là tham số) A) thay m=0 rồi giải pt đã cho B) tìm m để pt x^2+5x+3m=0 có 2 nghiệm phân biệt
a) Với m=0
=> pt <=> \(x^2+5x=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
b) \(x^2+5x+3m=0\)
\(\Delta=25-12m\)
Để phương trình có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow25-12m>0\)
\(\Leftrightarrow m< \dfrac{25}{12}\)
a,Cho pt bậc 2 ẩn x:x2 +2(2-m)x-3=0.Tìm m để pt có 2 nghiệm x1,x2 thỏa mãn Ix1x22I+Ix12x2I=18
b.Cho hàm số y=2x2(P).Viết pt đường thẳng đi qua điểm(0;2) và tiếp xúc vs (P)
Bài 1: Cho pt x2 + 13x -1 = 0 (1). Không giải pt, hãy lập một pt bậc hai có các nghiệm y1, y2 lớn hơn nghiệm của pt (1) là 2.
Bài 2: Cho pt x2 - 5x + 6 = 0 (1). Không giải pt, hãy lập pt bậc hai có các nghiệm y1 và y2 là:
a/ Số đối các nghiệm của pt (1).
b/ Nghịch đảo các nghiệm của pt (1).
2:
a: y1+y2=-(x1+x2)=-5
y1*y2=(-x1)(-x2)=x1x2=6
Phương trình cần tìm có dạng là;
x^2+5x+6=0
b: y1+y2=1/x1+1/x2=(x1+x2)/x1x2=5/6
y1*y2=1/x1*1/x2=1/x1x2=1/6
Phương trình cần tìm là:
a^2-5/6a+1/6=0
Tính đạo hàm của các hàm số sau:
a) \(y=x^4-\dfrac{3}{x}+\sqrt{x}-\dfrac{1}{x^2}\)
b) \(y=\dfrac{4sinx-3}{7-5sinx}\)
a.
\(y'=4x^3+\dfrac{3}{x^2}+\dfrac{1}{2\sqrt{x}}+\dfrac{2}{x^3}\)
b.
\(y'=\dfrac{\left(4sinx-3\right)'.\left(7-5sinx\right)-\left(7-5sinx\right)'.\left(4sinx-3\right)}{\left(7-5sinx\right)^2}\)
\(=\dfrac{4cosx\left(7-5sinx\right)+5cosx\left(4sinx-3\right)}{\left(7-5sinx\right)^2}\)
\(=\dfrac{13cosx}{\left(7-5sinx\right)^2}\)
cho pt bậc 2 : ax^2+bx+c=0 có 2 nghiệm phân biệt thỏa mãn
X1+x2-2.X1x2=0
mx1x2-(x1+x2)=2m+1
a) tìm pt bậc hai trên với m là tham số
b)xác định m để phương trình bậc 2 trên có 2 nghiệm dương phân biệt
viết lại câu hỏi khác đi, đề không rõ ràng X với x rồi . lung tung, dung công cụ soạn thảo đi nha bạn
Cho hàm số y = f(x), hàm số y = f ' x có đồ thị như hình vẽ bên. Hàm số g x = 2 f 5 sin x - 1 2 + 5 sin x - 1 2 4 + 3 có bao nhiêu cực trị trên khoảng (0; 2p ) ?
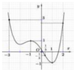
A. 9
B. 8
C. 7
D. 6