a) So sánh AD với AB+BD
b) Chứng minh: AD nhỏ hơn nửa chu vi ΔABC
Đọc tiếp
a) So sánh AD với AB+BD
b) Chứng minh: AD nhỏ hơn nửa chu vi ΔABC
Những câu hỏi liên quan
Cho ΔABC , góc A =90 độ , góc B=60độ .
a, So sánh AD và BD
b, Trên BC lấy D sao cho BD=AB . Qua D dựng đường vuông góc với BC cắt tia đối của AB tại E . Chứng minh : ΔABC=ΔDBE
c, H là giao điểm của AC và ED . Chứng minh : BH là phân giác của góc ABC
d, Qua B vẽ đường thẳng vuông góc AB cắt ED tại K . Chứng minh : ΔHBK đều
b) Xét ΔABC vuông tại A và ΔDBE vuông tại D có
AB=BD(gt)
\(\widehat{ABC}\) chung
Do đó: ΔABC=ΔDBE(cạnh góc vuông-góc nhọn kề)
c) Xét ΔBAH vuông tại A và ΔBDH vuông tại D có
BH chung
BA=BD(gt)
Do đó: ΔBAH=ΔBDH(Cạnh huyền-cạnh góc vuông)
Suy ra: \(\widehat{ABH}=\widehat{DBH}\)(hai góc tương ứng)
hay BH là tia phân giác của \(\widehat{ABC}\)
d) Ta có: BH là tia phân giác của \(\widehat{ABC}\)(cmt)
nên \(\widehat{ABH}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)
Ta có: \(\widehat{ABH}+\widehat{HBK}=90^0\)
\(\Leftrightarrow\widehat{HBK}+30^0=90^0\)
hay \(\widehat{HBK}=60^0\)
Xét ΔCHD vuông tại D và ΔCBA vuông tại A có
\(\widehat{ACB}\) chung
Do đó: ΔCHD\(\sim\)ΔCBA(g-g)
Suy ra: \(\widehat{CHD}=\widehat{CBA}\)(hai góc tương ứng)
\(\Leftrightarrow\widehat{CHD}=60^0\)
mà \(\widehat{CHD}=\widehat{HKB}\)(hai góc so le trong, BK//AC)
nên \(\widehat{HKB}=60^0\)
Xét ΔHBK có
\(\widehat{HKB}=60^0\)(cmt)
\(\widehat{HBK}=60^0\)(cmt)
Do đó: ΔHBK đều(Dấu hiệu nhận biết tam giác đều)
Đúng 0
Bình luận (1)
cho ΔABC có AB / AC tia phân giác AD chứng minh
a ADB<ADC
b trên AC lấy điểm E sao cho AE=AB gọi E là giao điểm của ED và AB chứng minh DE=DC
c so sánh BD và DC [mn giupa em với ạ]
a:AB<AC
=>góc C<góc B
=>góc C+góc CAD<góc B+góc BAD
=>góc ADB<góc ADC
b: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
=>ΔABD=ΔAED
=>BD=ED
c: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
mà AB<AC
nên BD<DC
Đúng 0
Bình luận (0)
cho ΔABC vuông tại A ,đường phân giác BD(DϵAC).Từ D kẻDH vuông góc với BC
a) chứng minh ΔABD=ΔHBD
b) so sánh AD và DC
a) Xét △ABD và △HBD có:
Góc BAD= Góc BHD (=90 độ)
BD chung
Góc ABD= Góc HBD (BD là phân giác góc ABC)
=>△ABD=△HBD (ch.gn) (đpcm)
b)=>AD=HD (2 cạnh tương ứng) (1)
Xét △HDC: Góc DHC=90 độ
=>DH<DC (2)
Từ (1),(2) =>AD<DC
Chúc bạn hok tốt!!!
Đúng 2
Bình luận (0)
Cho ΔABC vuông tại A có AB =9cm, BC =15 cm, vẽ AD ⊥ BC (D ⊥ BC).
a) Tính AC, so sánh BD và DC.
b) Trên đoạn thẳng DC lấy điểm N sao cho DB = DN. Chứng minh ΔABN lầ tam giác cân.
c) Kẻ BE ⊥ AN cắt AD tại H. Chứng minh NH ⊥ AB.
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=15^2-9^2=144\)
hay AC=12(cm)
Xét ΔABC có AB<AC(9cm<12cm)
mà hình chiếu của AB trên BC là DB
và hình chiếu của AC trên BC là DC
nên BD<DC
Đúng 1
Bình luận (0)
b) Xét ΔADB vuông tại D và ΔADN vuông tại D có
DB=DN(gt)
AD chung
Do đó: ΔADB=ΔADN(hai cạnh góc vuông)
Suy ra: AB=AN(Hai cạnh tương ứng)
Xét ΔABN có AB=AN(cmt)
nên ΔABN cân tại A(Định nghĩa tam giác cân)
Đúng 0
Bình luận (0)
c) Xét ΔANB có
BE là đường cao ứng với cạnh AN(gt)
AD là đường cao ứng với cạnh NB(Gt)
BE cắt AD tại H(gt)
Do đó: H là trực tâm của ΔANB(Tính chất ba đường cao của tam giác)
Suy ra: NH\(\perp\)AB(Đpcm)
Đúng 0
Bình luận (0)
bài 4: cho tam giác ABC cân tại A ( góc A nhỏ hơn 90 độ và AB nhỏ hơn BC) kẻ BD là tia phân giác của góc ABC (D thuộc AC ). Trên cạnh BC lấy điểm E sao cho AB = BE
a, vẽ hình
b,chứng minh tam giác ABD= tam giác EBD từ đó suy ra AD=DE
c,so sánh AD và DC
b: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>góc BED=90 độ và DA=DE
c: DA=DE
DE<DC
=>DA<DC
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
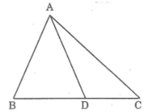
Trong ΔABD, ta có:
AD < AB + BD (bất đẳng thức tam giác) (1)
Trong ΔADC, ta có:
AD < AC + DC (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2), ta có:
2AD < AB + BD + AC + DC ⇔ 2AD < AB + AC + BC
Vậy AD < (AB + AC + BC) / 2 .
Đúng 1
Bình luận (0)
Cho tam giác ABC, điểm D nằm giữa B và C. Chứng minh rằng AD nhỏ hơn nửa chu vi tam giác ABC.
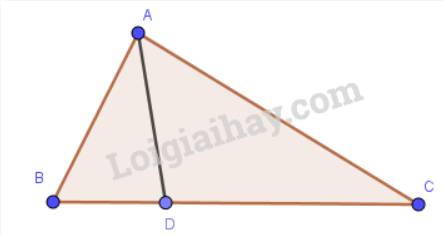
Áp dụng quan hệ giữa ba cạnh của tam giác ABD, ta có: AD < AB + BD
Áp dụng quan hệ giữa ba cạnh của tam giác ACD, ta có: AD < CD + AC
\(\Rightarrow AD + AD < AB+BD+CD+AC\)
\(\Rightarrow 2AD<AB+BC+AC\) ( vì \(DB+DC=BC\))
\(\Rightarrow\) 2AD < Chu vi tam giác ABC hay AD < (Chu vi tam giác ABC) : 2
Vậy AD nhỏ hơn nửa chu vi tam giác ABC.
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm D thuộc cạnh BC.
a) So sánh AD với BA + BD.
b) Chứng minh A D < A B + B C + C A 2
Tam giác ABC vuông cân tại A. D vừa nằm trên nửa mặt phẳng bờ AB chứa C, vừa nằm trên nửa mặt phẳng bờ AC không chứa B sao cho AB = AD(D khác c). Hạ CI vuông góc với BD.
a) So sánh chu vi tam giác ADB với chu vi hình tứ giác ABCI
b) Tìm vị trí điểm D sao cho chu vi hình tam giác DBC đạt giá trị Max
cho tứ giác ABCD ,chứng minh rằng :
a/ Tổng hai cạnh đối nhỏ hơn 2 cạnh chéo
b/Tổng 2 đường chéo thì lớn hơn nữa chu vi nhưng lnhỏ hoưn chu vi
c/Nếu AD+AC<BD+BC thì AD<BD
