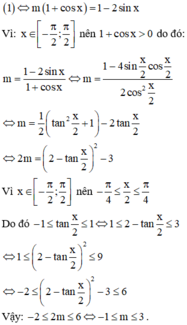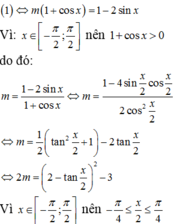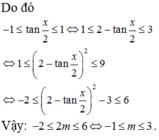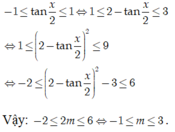Tìm m để phương trình \(2sinx+mcosx=1-m\) có nghiệm \(x\in\left[\dfrac{-\pi}{2};\dfrac{\pi}{2}\right]\)

Những câu hỏi liên quan
Tìm m để phương trình \(2sinx+mcosx=1-m\left(1\right)\) có nghiệm \(x\in\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\)
Tìm m để phương trình 2sinx +mcosx = 1-m có nghiệm x thuộc \(\left[\frac{-\pi}{2};\frac{\pi}{2}\right]\)
Tìm m để phương trình
2
sin
x
+
m
cos
x
1
−
m
có nghiệm
x
∈
−
π
2
;
π
2
. A.
−
2
≤
m
≤
6
B.
1
≤
m
≤
3
C....
Đọc tiếp
Tìm m để phương trình 2 sin x + m cos x = 1 − m có nghiệm x ∈ − π 2 ; π 2 .
A. − 2 ≤ m ≤ 6
B. 1 ≤ m ≤ 3
C. - 1 ≤ m ≤ 3
D. − 3 ≤ m ≤ 1
Tìm m để phương trình
2
sin
x
+
m
cos
x
1
-
m
có nghiệm
x
∈
-
π
2
;
π
2
Đọc tiếp
Tìm m để phương trình 2 sin x + m cos x = 1 - m có nghiệm x ∈ - π 2 ; π 2
![]()
![]()
![]()
![]()
Tìm m để phương trình 2sinx + mcosx 1 - m (1) có nghiệm
x
∈
-
π
2
;
π
2
. A. -3
≤
m
≤
1 B. -2
≤
m
≤
6 C. 1
≤
m
≤
3 D. -1
≤
m
≤...
Đọc tiếp
Tìm m để phương trình 2sinx + mcosx = 1 - m (1) có nghiệm x ∈ - π 2 ; π 2 .
A. -3 ≤ m ≤ 1
B. -2 ≤ m ≤ 6
C. 1 ≤ m ≤ 3
D. -1 ≤ m ≤ 3
Cho phương trình \(\left(cosx+1\right)\left(4cos2x-mcosx\right)=msin^2x\) . Số các giá trị nguyên của m để phương trình có đúng 2 nghiệm thuộc \(\left[0;\dfrac{2\pi}{3}\right]\) là
\(\Leftrightarrow\left(cosx+1\right)\left(4cos2x-m.cosx\right)=m\left(1-cosx\right)\left(1+cosx\right)\)
\(\Leftrightarrow4cos2x-m.cosx=m\left(1-cosx\right)\)
\(\Leftrightarrow4cos2x=m\)
\(\Rightarrow cos2x=\dfrac{m}{4}\)
Pt có đúng 2 nghiệm thuộc đoạn đã cho khi và chỉ khi:
\(-1< \dfrac{m}{4}\le-\dfrac{1}{2}\Leftrightarrow-4< m\le-2\)
Có 2 giá trị nguyên của m thỏa mãn
Đúng 0
Bình luận (0)
Tìm m để phương trình
f
x
0
có nghiệm. Biết
f
x
m
cos
x
+
2
sin
x
−
3
x
+
1
A.
m
0
B.
m
≥
5
C.
m
0
D.
−
5
m...
Đọc tiếp
Tìm m để phương trình f ' x = 0 có nghiệm. Biết f x = m cos x + 2 sin x − 3 x + 1
A. m > 0
B. m ≥ 5
C. m < 0
D. − 5 < m < 5
Đáp án B
f ' x = 0 ⇔ 2 cos x − m sin x = 3 *
Phương trình
f ' x = 0 ⇔ 2 cos x − m sin x = 3 *
Để (*) có nghiệm khi và chỉ khi
3 2 2 + − m 2 ≤ 1 ⇔ m 2 ≥ 5 ⇔ m ≤ 5
Đúng 0
Bình luận (0)
Tìm m để phương trình: cos2x + 2m.cosx - m + 1 = 0
1) Có nghiệm
2) Có nghiệm \(x\in\left(-\pi;-\dfrac{\pi}{3}\right)\)
Có bao nhiêu giá trị nguyên của tham số m để pt 2sinx + mcosx=1 - m có nghiệm thuộc [-pi/2; pi/2]