Chứng minh rằng
x2 - x + 3/4 > 0 với mọi giá trị của x
Chứng minh rằng: x 2 - x + 3 4 > 0 với mọi giá trị của x
Chứng minh rằng: Giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
Biểu thức x + 1 x 2 xác định khi x ≠ 0
Biểu thức x 2 + 1 x 2 + 2 x + 1 1 x + 1 xác định khi x ≠ 0 và x ≠ - 1
Với điều kiện x ≠ 0 và x ≠ - 1, ta có:
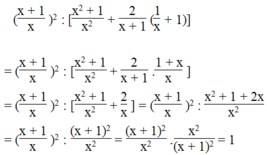
Vậy giá trị của biểu thức x + 1 x 2 : x 2 + 1 x 2 + 2 x + 1 1 x + 1 bằng 1 với mọi giá trị x ≠ 0 và x ≠ -1.
chứng tỏ các bất phương trình sau luôn nghiệm đungs với mọi x
x2 - 4x+5>0
chứng minh rằng -x2+4x-10/x2+1<0 với mọi x
tìm x để biểu thức x2-4x+5 đạt giá trị nhỏ nhất
tìm x để biểu thức -x2+4x+4 đạt giá trị lớn nhất
Ta có :
\(x^2-4x+5=\left(x^2-2.2x+2^2\right)+1=\left(x-2\right)^2+1\ge1>0\)
Vậy đa thức \(x^2-4x+5\) vô nghiệm với mọi giá trị của x
Chúc bạn học tốt ~
4. Tìm giá trị lớn nhất của các biểu thức a. A = 5 – 8x – x2 b. B = 5 – x2 + 2x – 4y2 – 4y 5. a. Cho a2 + b2 + c2 = ab + bc + ca chứng minh rằng a = b = c b. Tìm a, b, c biết a2 – 2a + b2 + 4b + 4c2 – 4c + 6 = 0 6. Chứng minh rằng: a. x2 + xy + y2 + 1 > 0 với mọi x, y b. x2 + 4y2 + z2 – 2x – 6z + 8y + 15 > 0 Với mọi x, y, z 7. Chứng minh rằng: x2 + 5y2 + 2x – 4xy – 10y + 14 > 0 với mọi x, y.
chứng minh rằng phương trình m(x-1)3(x2-4)+x4-3=0 luôn có ít nhất 2 nghiệm phân biệt với mọi giá trị m
Đặt \(f\left(x\right)=m\left(x-1\right)^3\left(x^2-4\right)+x^4-3\)
\(f\left(x\right)\) là hàm đa thức nên liên tục trên R
\(f\left(1\right)=-2< 0\)
\(f\left(2\right)=13>0\)
\(\Rightarrow f\left(1\right).f\left(2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (1;2)
\(f\left(-2\right)=13>0\Rightarrow f\left(1\right).f\left(-2\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc khoảng (-2;1)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 2 nghiệm phân biệt
Chứng minh rằng
-x2 + 8x - 19 < 0 với mọi giá trị x
\(-x^2+8x-19=-\left(x^2-8x+16\right)-3=-\left(x-4\right)^2-3\le-3< 0\)
cho biểu thức A = ( x - 3 ) ( x2 + 3x + 9 ) - ( x - 1 )3 + 4 ( x + 2 ) ( 2 - x ) - x
a. Chứng minh A = - x2 - 4x - 10
b. Chứng minh A luôn có giá trị âm với mọi giá trị của số thực x
a: \(A=x^3-27-x^3+3x^2-3x+1-4\left(x^2-4\right)-x\)
\(=3x^2-4x-26-4x^2+16\)
\(=-x^2-4x-10\)
Cho phương trình x2 - mx + m - 4 = 0 (x là ẩn ). Chứng minh rằng phương trình có hai nghiệm x1,x2 với mọi m. Tìm tất cả các giá trị nguyên dương của m để (5x1 - 1)(5x2 - 1 ) < 0
\(\Delta=m^2-4\left(m-4\right)=\left(m^2-4m+4\right)+12=\left(m-2\right)^2+12>0;\forall m\)
Suy ra pt luôn có hai nghiệm pb với mọi m
Theo viet có:\(\left\{{}\begin{matrix}x_1+x_2=m\\x_1.x_2=m-4\end{matrix}\right.\)
\(\left(5x_1-1\right)\left(5x_2-1\right)< 0\)
\(\Leftrightarrow25x_1x_2-5\left(x_1+x_2\right)+1< 0\)
\(\Leftrightarrow25\left(m-4\right)-5m+1< 0\)
\(\Leftrightarrow m< \dfrac{99}{20}\)
Vậy...
\(\Delta=m^2-4m+16=\left(m-2\right)^2+12>0\)
\(\Rightarrow\) pt luôn có 2 nghiệm phân biệt
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=m-4\end{matrix}\right.\)
Ta có: \(\left(5x_1-1\right)\left(5x_2-1\right)=25x_1x_2-5\left(x_1+x_2\right)+1\)
\(=25\left(m-4\right)-5m+1=20m-99\)
\(\Rightarrow20m-99< 0\Rightarrow m< \dfrac{99}{20}\)
chứng minh rằng x^4+2x^3-2x^2-10x+20 >0 với mọi giá trị của x
= (x2-x+1)(x2+3x+10)+10 = P
x2-x+1=(x-\(\frac{1}{2}\))2+\(\frac{3}{4}\)>0
x2+3x+10=(x+\(\frac{3}{2}\))2+\(\frac{31}{4}\)>0
vây P>0
Cho pt: x^2 +2(m-1)x-6m-7=0.(1)
a) Chứng minh rằng với mọi giá trị của m thì pt(1) luôn có hai nghiệm phân biệt.
b)Gọi x1,x2 là 2 nghiêm của phương trình:x^2 +2(m-1)x-6m-7=0. Tìm các giá trị của m để: x1(x1+3/2)+x2(x2+3/2x1)=15.
a) \(x^2+2\left(m-1\right)x-6m-7=0\)\(0\)
\(\left(a=1;b=2\left(m-1\right);b'=m-1;c=-6m-7\right)\)
\(\Delta'=b'^2-ac\)
\(=\left(m-1\right)^2-1.\left(-6m-7\right)\)
\(=m^2-2m+1+6m+7\)
\(=m^2+4m+8\)
\(=m^2+2.m.2+2^2+4\)
\(=\left(m+2\right)^2+4>0,\forall m\)
Vì \(\Delta'>0\) nên phương trình ( 1 ) luôn có 1 nghiệm phân biệt với mọi m