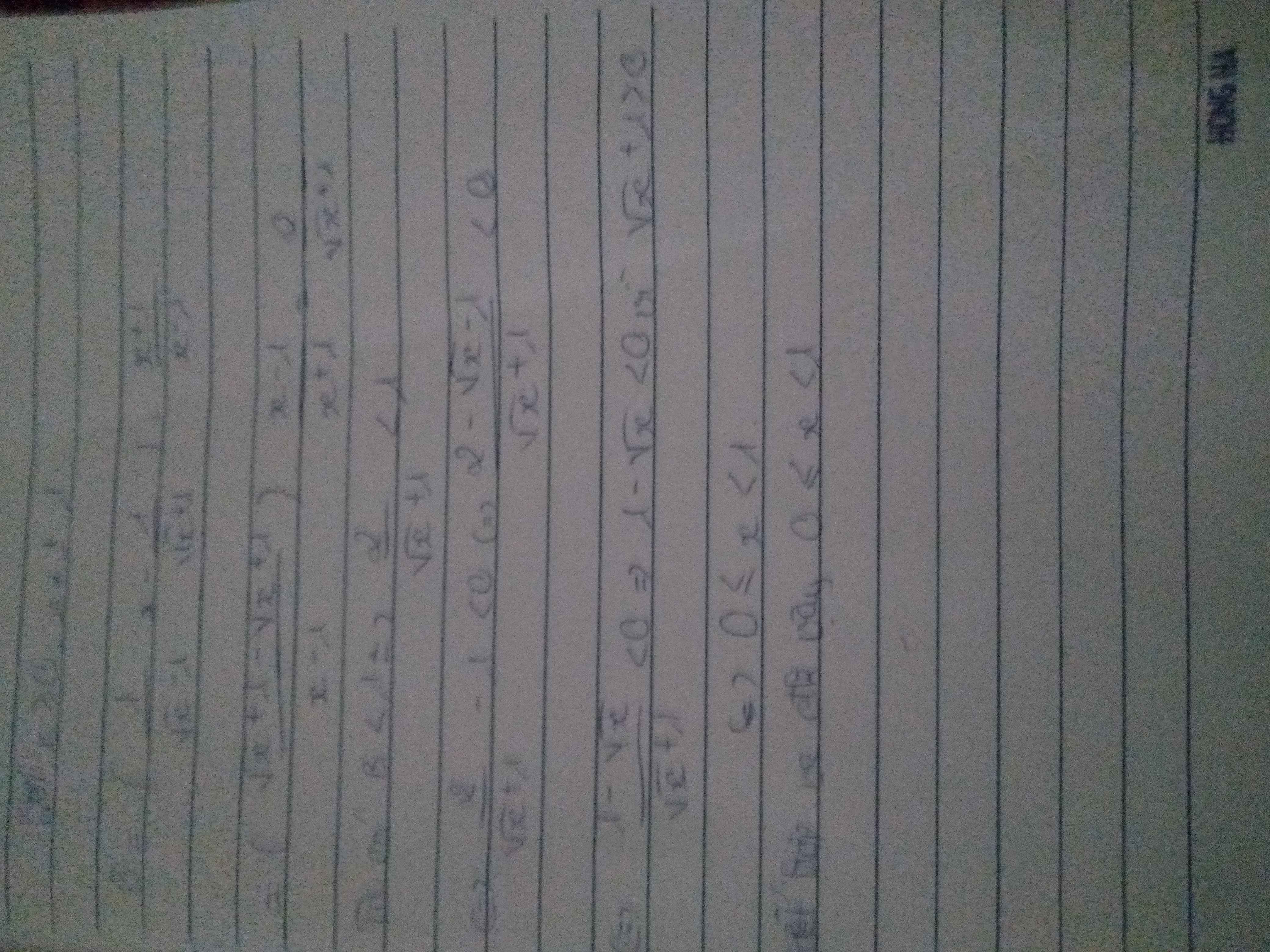Xét

\(1-\frac{\sqrt{x}+1}{x+\sqrt{x}+1}=\frac{x}{x+\sqrt{x}+1}\ge0\)

\(B=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x+1}{x-1}=\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x-1}{x+1}\)

\(=\dfrac{2}{x-1}.\dfrac{x-1}{x+1}=\dfrac{2}{x+1}\)

Để \(B< 1\Rightarrow\dfrac{2}{x+1}< 1\Rightarrow1-\dfrac{2}{x+1}>0\Rightarrow\dfrac{x-1}{x+1}>0\)

mà \(x+1>0\left(x\ge0\right)\Rightarrow x-1>0\Rightarrow x>1\)

a) Ta có: \(B=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x+1}{x-1}\)

\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{x+1}\)

\(=\dfrac{2}{x+1}\)

c,C= \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}\left(x\ge1\right)\)

=\(\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)

=\(\sqrt{x-1}+1+\left|\sqrt{x-1}-1\right|\) (1)

TH1: \(\sqrt{x-1}< 1\) hay \(1\le x< 2\)

Từ (1)=>C= \(\sqrt{x-1}+1+1-\sqrt{x-1}\)=2

TH2: \(\sqrt{x-1}\ge1\) hay \(x\ge2\)

Từ (1) =>C=\(\sqrt{x-1}+1+\sqrt{x-1}-1\)=\(2\sqrt{x-1}\)

d, D=\(\sqrt{13+30\sqrt{2}+\sqrt{9+4\sqrt{2}}}=\sqrt{13+30\sqrt{2}+\sqrt{8+2\sqrt{8}+1}}=\sqrt{13+30\sqrt{2}+\sqrt{\left(\sqrt{8}+1\right)^2}}\)

=\(\sqrt{13+30\sqrt{2}+\sqrt{8}+1}=\sqrt{14+30\sqrt{2}+2\sqrt{2}}\)

=\(\sqrt{14+32\sqrt{2}}\)

a)\(\frac{x-y}{\sqrt{x}-\sqrt{y}}=\frac{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}-\sqrt{y}}=\sqrt{x}+\sqrt{y}\)

b)\(\frac{x-2\sqrt{x}+1}{\sqrt{x}-1}=\frac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}=\sqrt{x}-1\)

Lời giải:

\(P=\frac{x+2}{(\sqrt{x})^3-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)}\)

\(\frac{x+2}{\sqrt{x^3}-1}+\frac{(\sqrt{x}+1)(\sqrt{x}-1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)}-\frac{1}{\sqrt{x}-1}\)

\(=\frac{x+2}{\sqrt{x^3}-1}+\frac{x-1}{\sqrt{x^3}-1}-\frac{1}{\sqrt{x}-1}\)

\(=\frac{x+2+x-1}{\sqrt{x^3}-1}-\frac{1}{\sqrt{x}-1}\)

\(=\frac{2x+1}{\sqrt{x^3}-1}-\frac{1}{\sqrt{x}-1}=\frac{2x+1}{\sqrt{x^3}-1}-\frac{x+\sqrt{x}+1}{\sqrt{x^3}-1}\)

\(=\frac{2x+1-(x+\sqrt{x})}{\sqrt{x^3}-1}=\frac{x-\sqrt{x}}{\sqrt{x^3}-1}\)

\(=\frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)}=\frac{\sqrt{x}}{x+\sqrt{x}+1}\)

b) \(P-\frac{1}{3}=\frac{\sqrt{x}}{x+\sqrt{x}+1}-\frac{1}{3}=\frac{2\sqrt{x}-(x+1)}{3(x+\sqrt{x}+1)}\)

\(=\frac{-(\sqrt{x}-1)^2}{3(x+\sqrt{x}+1)}\)

Với \(x\neq 1, x\geq 0\Rightarrow -(\sqrt{x}-1)^2< 0; x+\sqrt{x}+1>0\)

Do đó: \(P-\frac{1}{3}< 0\Rightarrow P< \frac{1}{3}\)

Để \(A=\frac{5}{\sqrt{x}-1}\)nguyên thì \(5⋮\sqrt{x}-1\)

\(\Rightarrow\sqrt{x}-1\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{2;0;6;-4\right\}\)

\(\Leftrightarrow x\in\left\{4;0;36\right\}\)( thỏa )

Để \(B=\frac{\sqrt{x}+1}{\sqrt{x}-3}\)nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)

\(\Leftrightarrow\sqrt{x}-3+4⋮\sqrt{x}-3\)

Vì \(\sqrt{x}-3⋮\sqrt{x}-3\)

\(\Rightarrow4⋮\sqrt{x}-3\)

\(\Rightarrow\sqrt{x}-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{4;2;5;1;7;-1\right\}\)

\(\Leftrightarrow x\in\left\{16;4;25;1;49\right\}\)

Máy kia tương tự đi ăn cơm đây :>

Mk lm nốt câu C

\(C=\frac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}=\frac{\sqrt{x}+2}{\sqrt{x}-1}=1+\frac{3}{\sqrt{x}-1}\)

Để C nguyên\(\Leftrightarrow\sqrt{x}-1\inƯ_{\left(3\right)}=\left\{\pm3;\pm1\right\}\)

\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=3\left(tm\right)\\\sqrt{x}-1=-3\left(l\right)\\\sqrt{x}-1=-1\left(tm\right)\\\sqrt{x}-1=1\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=16\\x=0\\x=4\end{matrix}\right.\)

câu này hay thế!

a: \(P=\dfrac{\sqrt{x}+1-2\sqrt{x}+4+2\sqrt{x}-7}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}=\dfrac{1}{\sqrt{x}+1}\)

b: căn x+1>=1

=>P<=1

Dấu = xảy ra khi x=0

a: 

Sửa đề: \(P=\left(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{3x+3}{9-x}\right)\cdot\left(\dfrac{\sqrt{x}-7}{\sqrt{x}+1}+1\right)\)

\(P=\left(\dfrac{2\sqrt{x}\left(\sqrt{x}-3\right)+\sqrt{x}\left(\sqrt{x}+3\right)-3x-3}{x-9}\right)\cdot\dfrac{\sqrt{x}-7+\sqrt{x}+1}{\sqrt{x}+1}\)

\(=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-3}{x-9}\cdot\dfrac{2\sqrt{x}-6}{\sqrt{x}+1}\)

\(=\dfrac{-3\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{2}{\sqrt{x}+1}=\dfrac{-6}{\sqrt{x}+3}\)

b: P>=1/2

=>P-1/2>=0

=>\(\dfrac{-6}{\sqrt{x}+3}-\dfrac{1}{2}>=0\)

=>\(\dfrac{-12-\sqrt{x}-3}{2\left(\sqrt{x}+3\right)}>=0\)

=>\(-\sqrt{x}-15>=0\)

=>\(-\sqrt{x}>=15\)

=>căn x<=-15

=>\(x\in\varnothing\)

c: căn x+3>=3

=>6/căn x+3<=6/3=2

=>P>=-2

Dấu = xảy ra khi x=0