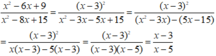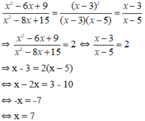Hướng dẫn giải:

a, 7x - 14

= 7(x-2)

b, 2x - 2y + \(x^2\)- xy 

= (2x-2y) + (\(x^2\)-xy)

= 2(x-y) + x(x-y)

= (x-y)(2+x)

c, 6x + 12

= 6(x+2)

\(a,=7\left(x-2\right)\\ b,=2\left(x-y\right)+x\left(x-y\right)=\left(x+2\right)\left(x-y\right)\\ c,=6\left(x+2\right)\\ d,\text{Sai đề}\)

1)(x²-4x+16)(x+4)-x(x+1)(x+2)+3x²=0

\(\Rightarrow\)(x³+64)-x(x²+2x+x+2)+3x²=0

\(\Rightarrow\)x³+64-x³-2x²-x²-2x+3x²=0

\(\Rightarrow\)-2x+64=0

\(\Rightarrow\)-2x=-64

\(\Rightarrow\)x=\(\dfrac{-64}{-2}\)

\(\Rightarrow x=32\)

2)(8x+2)(1-3x)+(6x-1)(4x-10)=-50

\(\Rightarrow\)8x-24x²+2-6x+24x²-60x-4x+10=50

\(\Rightarrow\)-62x+12=50

\(\Rightarrow\)-62x=50-12

\(\Rightarrow\)-62x=38

\(\Rightarrow\)x=\(-\dfrac{38}{62}=-\dfrac{19}{31}\)

3)(x²+2x+4)(2-x)+x(x-3)(x+4)-x²+24=0

\(\Rightarrow\)8-x³+x(x²+4x-3x-12)-x²+24=0

\(\Rightarrow\)8-x³+x³+4x²-3x²-12x-x²+21=0

\(\Rightarrow\)-12x+29=0

\(\Rightarrow\)-12x=-29

\(\Rightarrow\)x=\(\dfrac{-29}{-12}=\dfrac{29}{12}\)

a) = 2(x-2)^2

b) = 4(x - y) + (x - y)(x + y)

= (x - y)(x + y + 4)

c) = (x - 2)(x - 4)

\(2\left(x-2\right)^2\)

\(\left(4+x+y\right)\left(x-y\right)\)

a: \(2x^2-8x+8=2\left(x-2\right)^2\)

b: \(4x-4y+x^2-y^2\)

\(=4\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)

\(=\left(x-y\right)\left(4+x+y\right)\)

c: \(x^2-6x+8=\left(x-2\right)\left(x-4\right)\)

Bài 6:

a) Ta có: \(A=-x^2+6x-11\)

\(=-\left(x^2-6x+11\right)\)

\(=-\left(x-3\right)^2-2\le-2\forall x\)

Dấu '=' xảy ra khi x=3

b) Ta có: \(B=-x^2-8x+5\)

\(=-\left(x^2+8x-5\right)\)

\(=-\left(x^2+8x+16-21\right)\)

\(=-\left(x+4\right)^2+21\le21\forall x\)

Dấu '=' xảy ra khi x=-4

c) Ta có: \(C=-x^2+4x+1\)

\(=-\left(x^2-4x-1\right)\)

\(=-\left(x^2-4x+4-5\right)\)

\(=-\left(x-2\right)^2+5\le5\forall x\)

Dấu '=' xảy ra khi x=2

Bài 7:

a) Ta có: \(x^2-6x+11\)

\(=x^2-6x+9+2\)

\(=\left(x-3\right)^2+2\ge2\forall x\)

Dấu '=' xảy ra khi x=3

Đáp án: A

ĐKXĐ: x ≠ 3; x ≠ 5.

Ta có:

Bài 1:

a: \(A=x^2+2x+4\)

\(=x^2+2x+1+3\)

\(=\left(x+1\right)^2+3>=3\forall x\)

Dấu '=' xảy ra khi x+1=0

=>x=-1

Vậy: \(A_{min}=3\) khi x=-1

b: \(B=x^2-20x+101\)

\(=x^2-20x+100+1\)

\(=\left(x-10\right)^2+1>=1\forall x\)

Dấu '=' xảy ra khi x-10=0

=>x=10

Vậy: \(B_{min}=1\) khi x=10

c: \(C=x^2-2x+y^2+4y+8\)

\(=x^2-2x+1+y^2+4y+4+3\)

\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)

Dấu '=' xảy ra khi x-1=0 và y+2=0

=>x=1 và y=-2

Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)

Bài 2:

a: \(A=5-8x-x^2\)

\(=-\left(x^2+8x\right)+5\)

\(=-\left(x^2+8x+16-16\right)+5\)

\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)

Dấu '=' xảy ra khi x+4=0

=>x=-4

b: \(B=x-x^2\)

\(=-\left(x^2-x\right)\)

\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)

\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)

Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)

=>\(x=\dfrac{1}{2}\)

c: \(C=4x-x^2+3\)

\(=-x^2+4x-4+7\)

\(=-\left(x^2-4x+4\right)+7\)

\(=-\left(x-2\right)^2+7< =7\forall x\)

Dấu '=' xảy ra khi x-2=0

=>x=2

d: \(D=-x^2+6x-11\)

\(=-\left(x^2-6x+11\right)\)

\(=-\left(x^2-6x+9+2\right)\)

\(=-\left(x-3\right)^2-2< =-2\forall x\)

Dấu '=' xảy ra khi x-3=0

=>x=3

a) 

\(x^3+\left(x-5\right)\left(x+8\right)=2x^2-37\\ \Leftrightarrow x^3+x^2+3x-40=2x^2-37\\ \Leftrightarrow x^3-x^2+3x-3=0\\ \Leftrightarrow x^2\left(x-3\right)+3\left(x-3\right)=0\\ \Leftrightarrow\left(x^2+3\right)\left(x-3\right)=0\)

Vì \(x^2+3\ge3>0\Rightarrow x-3=0\\ \Leftrightarrow x=3\)

b)

\(x\left(x-1\right)\left(x+1\right)\left(x+2\right)=24\\ \Leftrightarrow\left[x\left(x+1\right)\right]\left[\left(x-1\right)\left(x+2\right)\right]=24\\ \Leftrightarrow\left(x^2+x\right)\left(x^2+x-2\right)=24\)

Đặt \(x^2+x=y\)

\(\Rightarrow y\left(y-2\right)=24\\ \Leftrightarrow y^2-2y+1=25\\ \Leftrightarrow\left(y-1\right)^2=25\\ \Leftrightarrow\left[{}\begin{matrix}y-1=5\\y-1=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}y=6\\y=-4\end{matrix}\right.\)

Nếu y = 6 

\(\Rightarrow x^2+x=6\\ \Leftrightarrow x^2+x-6=0\\ \Leftrightarrow x^2+2x-3x-6=0\\ \Leftrightarrow x\left(x+2\right)-3\left(x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

Nếu y = -4

\(\Rightarrow x^2+x=-4\\ \Leftrightarrow x^2+x+\dfrac{1}{4}=-4+\dfrac{1}{4}\\ \Leftrightarrow\left(x+\dfrac{1}{2}\right)^2=-\dfrac{15}{4}\)

Mà \(\left(x+\dfrac{1}{.2}\right)^2\ge0>-\dfrac{15}{4}\)

`=> Loại`

c) Vế còn lại là bao nhiêu?

a: \(x^2-6x+5=\left(x-5\right)\left(x-1\right)\)

b: \(x^2-x-12=\left(x-4\right)\left(x+3\right)\)

c: \(x^2+8x+15=\left(x+5\right)\left(x+3\right)\)

d: \(2x^2-5x-12=\left(x-4\right)\left(2x+3\right)\)

e: \(x^2-13x+36=\left(x-9\right)\left(x-4\right)\)