Cho hình vẽ. Chứng minh rằng \(\widehat{xAc}\)= \(\widehat{B}+\widehat{C}\)

Những câu hỏi liên quan
Bài 2: (Vẽ hình) Cho widehat{xOy}. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OAOB. Gọi C là 1 điểm trên tia phân giác Oz của widehat{xOy}. Chứng minh rằng:a, ACBCwidehat{xAC}widehat{yBC}b, OCOB
Đọc tiếp
Bài 2: (Vẽ hình) Cho \(\widehat{xOy}\). Trên tia \(Ox\) lấy điểm \(A\), trên tia \(Oy\) lấy điểm \(B\) sao cho \(OA=OB\). Gọi \(C\) là 1 điểm trên tia phân giác \(Oz\) của \(\widehat{xOy}\). Chứng minh rằng:
a, \(AC=BC\)
\(\widehat{xAC}=\widehat{yBC}\)
b, \(OC=OB\)
`a,`
Xét $\Delta OAC$ và $\Delta ABC$ ta có `:`
`OA=OB(gt)`
\(\widehat{AOC}=\widehat{BOC}\) `( Oz` là tia phân giác \(\widehat{B}\) `)`
Chung `Oz`
`=>` $\Delta OAC$ `=` $\Delta ABC$ `(c.g.c)`
`=>` `{(\hat{OAC}=\hat{OBC} \text{( 2 góc tương ứng )} ),(AC=BC \text{ (2 cạnh tương ứng)}):}`
Từ `\hat{OAC}=\hat{OBC}`
`=>` `\hat{xAC}=\hat{yBC}` `(` kề bù với `2` góc bằng nhau `)`
`b,` Xem lại đề bài `: OC=OB?`
Đúng 3
Bình luận (0)
Cho hình vẽ, biết rằng CD//Eywidehat{BAx} 1400 , widehat{ABD} 400 , widehat{BEy} 1300a, tính widehat{CBE} ?b, chứng minh Ax // Eyc, chứng minh ABperpBE thêm vào hình vẽ: widehat{B_1} 400, widehat{A_1} 1400 , widehat{E_1} 1300A x y E B C D
Đọc tiếp
Cho hình vẽ, biết rằng CD//Ey
\(\widehat{BAx}\)= 1400 , \(\widehat{ABD}\)= 400 , \(\widehat{BEy}\)= 1300
a, tính \(\widehat{CBE}\) ?
b, chứng minh Ax // Ey
c, chứng minh AB\(\perp\)BE thêm vào hình vẽ: \(\widehat{B_1}\)= 400, \(\widehat{A_1}\)= 1400 , \(\widehat{E_1}\)= 1300
A x y E B C D
a) Ta có: CD//Ey
\(\Rightarrow\widehat{CBE}=\widehat{E_1}=130^0\)(so le trong)
b) Ta có: Ta có: CD//Ey
\(\Rightarrow\widehat{EBD}+\widehat{E_1}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{EBD}=180^0-\widehat{E_1}=50^0\)
Ta có: \(\widehat{EBD}+\widehat{B_1}=50^0+40^0=90^0\)
=> AB⊥BE
Đúng 0
Bình luận (0)
Cho hình vẽ, biết Ax//By và \(\widehat{CBy}\) \(>\widehat{ACB.}\) Chứng minh rằng \(\widehat{yBC}\)\(=\widehat{xAC}\)\(+\widehat{ACB}\)

Gọi By' là tia đối của tia By.
Gọi I là giao điểm của AC và yy'
By//Ax (gt) nên By'//Ax
Do By'//Ax nên xAC=AIy' ( so le trong)
Ta lại có: AIy=BIC ( đối đỉnh)
Do yBC là góc ngoài tại đỉnh B của tam giác BCI nên:
yBC=BIC+ACB
Mà xAC=AIy'
BIC=AIy'
=> xAC=BIC
Do đó yBC=xAC+ACB (đpcm)
Đúng 0
Bình luận (0)
11: Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho
\(\widehat{EDC}=\widehat{ECD}=15^o\)
a) Vẽ điểm F trong hình vuông sao cho \(\widehat{FAD}=\widehat{FDA}=15^o\) . Chứng minh rằng tam
giác DEF là tam giác đều.
b) Chứng minh rằng tam giác ABE là tam giác đều.
Cho hình vuông ABCD. Vẽ điểm E trong hình vuông sao cho \(\widehat{EDC}=\widehat{ECD}=15^0\)
a) Vẽ điểm F trong hình vuông sao cho \(\widehat{FAD}=\widehat{FDA}=15^0\)
Chứng minh tam giác DEF là tam giác đều
b) Chứng minh rằng tam giác ABE là tam giác đều
Cho tam giác ABC vuông tại A. Dựng điểm D trên cạnh AC sao cho widehat{DBC}frac{1}{3}widehat{ABC}. Gọi X là hình chiếu vuông góc của C trên đường thẳng BD. Trên tia BA lấy điểm Y sao cho BX BY. Chứng minh rằng a) frac{1}{BY^2}+frac{1}{CX^2}frac{4}{XY^2}b) widehat{XAC}widehat{DBC}từ đó suy ra AX XYc) coswidehat{ABC}4cos^2frac{widehat{ABC}}{3}-3cosfrac{widehat{ABC}}{3}
Đọc tiếp
Cho tam giác ABC vuông tại A. Dựng điểm D trên cạnh AC sao cho \(\widehat{DBC}=\frac{1}{3}\widehat{ABC}\). Gọi X là hình chiếu vuông góc của C trên đường thẳng BD. Trên tia BA lấy điểm Y sao cho BX = BY. Chứng minh rằng
a) \(\frac{1}{BY^2}+\frac{1}{CX^2}=\frac{4}{XY^2}\)
b) \(\widehat{XAC}=\widehat{DBC}\)từ đó suy ra AX = XY
c) \(cos\widehat{ABC}=4cos^2\frac{\widehat{ABC}}{3}-3cos\frac{\widehat{ABC}}{3}\)
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
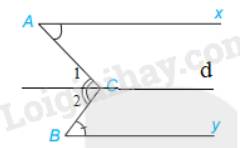
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
Đúng 0
Bình luận (0)
Câu 1: Cho Delta ABC;widehat{A}100^0;widehat{B}40^0. Vẽ tia đối của AB là tia Ax. Vẽ tia AI là tia phân giác của widehat{xAC}
a) Chứng minh Ay // BC
b) Tính widehat{ACB}
Câu 2: Cho Delta ABC có widehat{A}90^0. Kẻ AHperp BCleft(Hin BCright). Kẻ HEperp ACleft(Ein ACright)
a) Chứng minh AB // HE
b) Biết widehat{B}60^0. Tính widehat{AHE};widehat{BAH}
Đọc tiếp
Câu 1: Cho \(\Delta ABC;\widehat{A}=100^0;\widehat{B}=40^0\). Vẽ tia đối của AB là tia Ax. Vẽ tia AI là tia phân giác của \(\widehat{xAC}\)
a) Chứng minh Ay // BC
b) Tính \(\widehat{ACB}\)
Câu 2: Cho \(\Delta ABC\) có \(\widehat{A}=90^0\). Kẻ \(AH\perp BC\left(H\in BC\right).\) Kẻ \(HE\perp AC\left(E\in AC\right)\)
a) Chứng minh AB // HE
b) Biết \(\widehat{B}=60^0.\) Tính \(\widehat{AHE};\widehat{BAH}\)
Câu 1
a.
Xét \(\Delta ABC\) có :
\(\widehat{ABC}+\widehat{BAC}+\widehat{BCA}=180^o\) ( định lý tổng 3 góc của 1 \(\Delta\) )
\(\Rightarrow\widehat{BCA}=40^o\) (1)
Ta có Ax là tia đối của AB
suy ra \(\widehat{BAC}+\widehat{CAx}=180^o\)
\(\widehat{CAx}=80^o\)
lại có Ay là tia phân giác \(\widehat{CAx}\)
\(\Rightarrow\widehat{xAy}=\widehat{yAc}=\dfrac{\widehat{CAx}}{2}=\dfrac{80^o}{2}=40^o\) (2)
Từ (1)(2) suy ra \(\widehat{yAc}=\widehat{ACB}=40^o\)
mà chúng ở vị trí so le trong
\(\Rightarrow\) Ay//BC
Bài 2
Rảnh làm sau , đến giờ học rồi .
Đúng 0
Bình luận (0)
1.Cho hình 16:a) Cho biết Ax//Cy.So sánh widehat{ABC} với widehat{A} và widehat{C}b) Cho biết widehat{ABC}widehat{A} vàwidehat{C} . Chứng tỏ rằng Ax// Cy x y B A C Hình 16 Hình 16
Đọc tiếp
1.Cho hình 16:
a) Cho biết \(Ax//Cy.So\) \(sánh \)\(\widehat{ABC}\) với \(\widehat{A}\) và \(\widehat{C}\)
b) Cho biết \(\widehat{ABC}\)=\(\widehat{A}\) và\(\widehat{C}\) . Chứng tỏ rằng \(Ax//\) Cy






















