Cho hàm số \(y=f\left(x\right)=\dfrac{2}{x^2+1}\)
a.Cmr hàm số đồng biến trong khoảng (0;1)
b.Cmr hàm số nghịch biến với mọi x>1
Những câu hỏi liên quan
Cho hàm số \(y=f\left(x\right)\) liên tục trên R, có đạo hàm \(f'\left(x\right)=x\left(x-1\right)^2\left(x-2\right)\) . Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho hàm số \(y=f\left(\dfrac{x+2}{x+m}\right)\) đồng biến trên khoảng \(\left(10;+\infty\right)\) . Tính tổng các phần tử của S.
11 tháng 11 2023 lúc 0:22
Câu 48: Cho hàm số yf(x) có đạo hàm liên tục trên R và fleft(xright)xleft(2x-1right)left(x^2+3right)+2. Hàm số yfleft(3-xright)+2x+2023 đồng biến trên khoảng nào trong các khoảng sau?A: left(-infty;3right)B: (3;5)C: (2;5/2)D: (5/2;3)Câu 50: Cho hàm số yf(x) có đạo hàm fleft(xright)left(x-1right)^2cdotleft(x^2-2xright) với forall xin R. Có bao nhiêu giá trị nguyên dương của tham số m để hàm số fleft(x^2-8x+mright) có 5 điểm cực trị?
Đọc tiếp
Câu 48: Cho hàm số y=f(x) có đạo hàm liên tục trên R và \(f'\left(x\right)=x\left(2x-1\right)\left(x^2+3\right)+2\). Hàm số \(y=f\left(3-x\right)+2x+2023\) đồng biến trên khoảng nào trong các khoảng sau?
A: \(\left(-\infty;3\right)\)
B: (3;5)
C: (2;5/2)
D: (5/2;3)
Câu 50: Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=\left(x-1\right)^2\cdot\left(x^2-2x\right)\) với \(\forall x\in R\). Có bao nhiêu giá trị nguyên dương của tham số m để hàm số \(f\left(x^2-8x+m\right)\) có 5 điểm cực trị?
Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=x\left(x+1\right)^2\left(x^2+2mx+1\right)\) với mọi x thuộc R. Có bao nhiêu số nguyên âm m để hàm số \(g\left(x\right)=f\left(2x+1\right)\) đồng biến trên khoảng (3;5)
Cho hàm số: \(y=-\dfrac{x^3}{3}+\left(a-1\right)x^2+\left(a+3\right)x-4\). Tìm a để hàm số đồng biến trên khoảng (0;3)
\(y'=-x^2+2\left(a-1\right)x+a+3\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x\in\left(0;3\right)\) ta có:
\(-x^2+2\left(a-1\right)x+a+3\ge0\)
\(\Leftrightarrow\left(2x+1\right)a\ge x^2+2x-3\)
\(\Rightarrow a\ge\dfrac{x^2+2x-3}{2x+1}\)
Xét hàm \(f\left(x\right)=\dfrac{x^2+2x-3}{2x+1}\) với \(x\in\left(0;3\right)\)
\(f'\left(x\right)=\dfrac{2\left(x^2+x+4\right)}{\left(2x+1\right)^2}>0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)< f\left(3\right)=\dfrac{12}{7}\Rightarrow a\ge\dfrac{12}{7}\)
Đúng 0
Bình luận (0)
Cho f(x) là hàm số bậc 4 thỏa mãn fleft(0right)dfrac{-1}{ln2}. Hàm số fleft(xright) có bảng biến thiên như sau: Hàm số gleft(xright)left|fleft(-x^2right)-x^2+dfrac{2^{x^2}}{ln2}right| có bao nhiêu điểm cực trị?A. 3B.2C.4D.5
Đọc tiếp
Cho f(x) là hàm số bậc 4 thỏa mãn \(f\left(0\right)=\dfrac{-1}{\ln2}\). Hàm số \(f'\left(x\right)\) có bảng biến thiên như sau:
Hàm số \(g\left(x\right)=\left|f\left(-x^2\right)-x^2+\dfrac{2^{x^2}}{\ln2}\right|\) có bao nhiêu điểm cực trị?
A. 3
B.2
C.4
D.5
Mình nghĩ là câu B.2 (Mình ko chắc lắm 
)
Đúng 1
Bình luận (0)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như Hình 9. Chỉ ra khoảng đồng biến và khoảng nghịch biến của hàm số \(y = f\left( x \right)\).
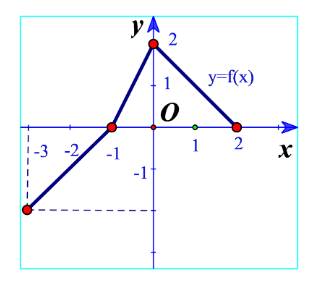
Từ đồ thị hàm số ta thấy khi x tăng từ -3 đến -1 và từ -1 đến 0 thì đồ thị đi lên nên hàm số đồng biến trên các khoảng (-3;-1) và (-1;0).
Khi x tăng từ 0 đến 2 thì đồ thị đi xuống nên hàm số nghịch biến trên (0;2).
Đúng 0
Bình luận (0)
Cho hàm số \(y=\left(2-m\right)x^2\) \(\left(m\ne\dfrac{3}{2}\right)\)
Tìm m để hàm số đồng biến khi x<0
Cho hàm số \(y=\dfrac{x^3}{3}-\left(m-1\right)x^2+3\left(m-1\right)x+1\). Có tất cả bao nhiêu giá trị nguyên của tham số m để hàm số đã cho đồng biến trên khoảng \(\left(1;+\infty\right)\)
\(y'=x^2-2\left(m-1\right)x+3\left(m-1\right)\)
Hàm đồng biến trên khoảng đã cho khi với mọi \(x>1\) ta luôn có:
\(g\left(x\right)=x^2-2\left(m-1\right)x+3\left(m-1\right)\ge0\)
\(\Rightarrow\min\limits_{x>1}g\left(x\right)\ge0\)
Do \(a=1>0;-\dfrac{b}{2a}=m-1\)
TH1: \(m-1\ge1\Rightarrow m\ge2\)
\(\Rightarrow g\left(x\right)_{min}=f\left(m-1\right)=\left(m-1\right)^2-2\left(m-1\right)^2+3\left(m-1\right)\ge0\)
\(\Rightarrow\left(m-1\right)\left(4-m\right)\ge0\Rightarrow1\le m\le4\Rightarrow2\le m\le4\)
TH2: \(m-1< 1\Rightarrow m< 2\Rightarrow g\left(x\right)_{min}=g\left(1\right)=m\ge0\)
Vậy \(0\le m\le4\)
Đúng 0
Bình luận (0)
1. Cho hàm số y =f(x) có đạo hàm f'(x) = (x^2 -1)(x-2)^2(x-3) . Hàm số đồng biến ; nghịch biến trên khoảng nào? 2. Cho hàm số y = x^4 -2x^2 . Hàm số đồng biến ; nghịch biến trên khoảng nào?
1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)
Đúng 0
Bình luận (0)