Lời giải:

\(A\cap B = (-3; 1)\)

P/s: Những bài này bạn cứ vẽ trục số ra rất dễ hình dung để làm.

Lời giải:
Theo đề thì: \(B\subset A\) nên \(A\cap B = B [-2;1)\)

A=[-4;4]

B=[-3;2)

\(A\cap B\)=[-3;2)

A\B=[-4;-3)

B\A=\(\varnothing\)

Ta có: \(A = \left\{ {x \in \mathbb{Z}| - 2 \le x \le 3} \right\} = \{  - 2; - 1;0;1;2;3\} \)

Và \(B = \{ x \in \mathbb{R}|{x^2} - x - 6 = 0\}  = \{  - 2;3\} \)

Khi đó:

Tập hợp \(A\,{\rm{\backslash }}\,B\) gồm các phần tử thuộc A mà không thuộc B. Vậy\(A\,{\rm{\backslash }}\,B = \{  - 1;0;1;2\} \).

 Tập hợp \(B\,{\rm{\backslash }}\,A\) gồm các phần tử thuộc B mà không thuộc A. Vậy \(B\,{\rm{\backslash }}\,A = \emptyset \)

\(A\cup B=\left(-1;+\infty\right)\)

\(A\cap B=(2;5]\)

Tham khảo:

Ta có:

Bất phương trình \(1 - 2x \le 0\) có nghiệm là \(x \ge \frac{1}{2}\) hay \(A = [\frac{1}{2};+\infty)\)

Bất phương trình \(x - 2 < 0\) có nghiệm là \(x < 2\) hay \(B = ( - \infty ;2)\)

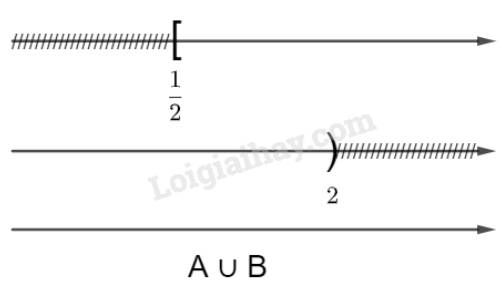
Vậy \(A \cup B = \mathbb R\)

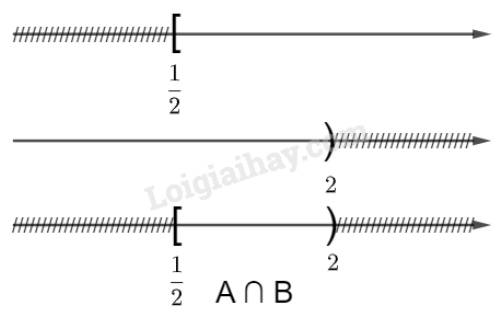
Vậy \(A \cap B = [\frac{1}{2};2)\)

Tham khảo: 

a) Tập hợp A là khoảng (-2;1) và được biểu diễn là:

b) Tập hợp B là đoạn [-3; 0] và được biểu diễn là:

c) Tập hợp B là nửa khoảng \(( - \infty ;1]\) và được biểu diễn là:

d) Tập hợp B là nửa khoảng \((-2; - \infty )\) và được biểu diễn là:

\(\left|x-1\right|< 3\Leftrightarrow-3< x-1< 3\Leftrightarrow-2< x< 4\)

\(\Rightarrow A=\left(-2;4\right)\)

\(\left|x+2\right|>5\Rightarrow\left[{}\begin{matrix}x+2>5\\x+2< -5\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x>3\\x< -7\end{matrix}\right.\)

\(\Rightarrow B=\left(-\infty;-7\right)\cup\left(3;+\infty\right)\)

\(A\cup B=\left(-\infty;-7\right)\cup\left(-2;+\infty\right)\)

\(A\cap B=\left(3;4\right)\)

A=(0;+\(\infty\))

B=[-3;15)

\(A\cup B=[-3;+\infty)\)