Cho \(0^o< a< b< 90^o\). Chứng minh: \(\sin a< \sin b\)

Những câu hỏi liên quan
Tìm các giá trị lượng giác còn lại biết:
a) Cho sin \(x=-\dfrac{4}{5}\)và \(90^o< x< 180^o\)
b) Cho \(\sin x=\dfrac{\sqrt{3}}{2}\)và \(270^o< x< 360^o\)
c) Cho \(\cos x=-\dfrac{1}{3}\)và \(0^o< x< 90^o\)
a: Sửa đề: sin x=4/5
cosx=-3/5; tan x=-4/3; cot x=-3/4
b: 270 độ<x<360 độ
=>cosx>0
=>cosx=1/2
tan x=căn 3; cot x=1/căn 3
Đúng 0
Bình luận (0)
Chứng minh các hệ thức sau:
a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
Tham khảo:
a)
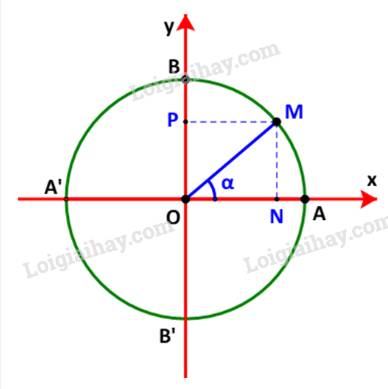
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM =1). (đpcm)
Đúng 0
Bình luận (0)
b)
Ta có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\;\;(\alpha \ne {90^o})\)
\( \Rightarrow 1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\) (đpcm)
c)
Ta có: \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}\;\;\;({0^o} < \alpha < {180^o})\)
\( \Rightarrow 1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha }}{{{{\sin }^2}\alpha }} + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }}\)
Mà theo ý a) ta có \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) với mọi góc \(\alpha \)
\( \Rightarrow 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\) (đpcm)
Đúng 0
Bình luận (0)
chứng minh rằng: \(\sqrt{\frac{1+sin\alpha}{1-sin\alpha}}-\sqrt{\frac{1-sin\alpha}{1+sin\alpha}}=2tan\alpha\) với \(0^o< \alpha< 90^o\)
\(\sqrt{\frac{1+\sin}{1-\sin}}-\sqrt{\frac{1-\sin}{1+\sin}}\)
\(=\sqrt{\frac{1-\sin^2}{\left(1-\sin\right)^2}}-\sqrt{\frac{1-\sin^2}{\left(1+\sin\right)^2}}\)
\(=\sqrt{\frac{\cos^2}{\left(1-\sin\right)^2}}-\sqrt{\frac{\cos^2}{\left(1+\sin\right)^2}}\)
\(=\frac{\cos}{1-\sin}-\frac{\cos}{1+\sin}=\cos.\left(\frac{1}{1-\sin}-\frac{1}{1+\sin}\right)\)
\(=\cos.\frac{2\sin}{1-\sin^2}=\frac{2\sin\cos}{\cos^2}=\frac{2\sin}{\cos}=2\tan\)
Đúng 0
Bình luận (0)
xem quá thôi cái này vượt quá xa (có phải toán lớp 9 đâu), không dám động vào
Đúng 0
Bình luận (0)
Cho \(0^o< \alpha< 90^0\)
a) Có giá trị nào của \(\alpha\) sao cho \(\tan\alpha< \sin\alpha\) hay không ?
b) Chứng minh rằng \(\sin\alpha+\cos\alpha>1\)
a)Do \(0^o< \alpha< 90^o\) nên \(0< sin\alpha< 1;0< cos\alpha< 1\).
Giả sử: \(tan\alpha< sin\alpha\Leftrightarrow\dfrac{sin\alpha}{cos\alpha}< sin\alpha\)
\(\Leftrightarrow sin\alpha< sin\alpha cos\alpha\)
\(\Leftrightarrow sin\alpha\left(1-cos\alpha\right)< 0\)
\(\Leftrightarrow1-cos\alpha< 0\)
\(\Leftrightarrow cos\alpha>1\) (vô lý).
b) \(sin\alpha+cos\alpha=sin\alpha+sin\left(\dfrac{\pi}{2}-\alpha\right)\)
\(=2.sin\dfrac{\pi}{4}cos\left(\dfrac{\pi}{4}-\alpha\right)=\sqrt{2}cos\left(\dfrac{\pi}{4}-\alpha\right)\)
\(=\sqrt{2}sin\left(\dfrac{\pi}{4}+\alpha\right)=\sqrt{2}sin\left(45^o+\alpha\right)\).
Do \(0^o< \alpha< 90^o\) nên \(45^o< \alpha+45^o< 135^o\).
Vì vậy \(\dfrac{\sqrt{2}}{2}< sin\left(\alpha+45^o\right)< 1\).
Từ đó suy ra \(\sqrt{2}.sin\left(45^o+\alpha\right)>\sqrt{2}.\dfrac{\sqrt{2}}{2}=1\) (Đpcm).
Đúng 0
Bình luận (0)
Chứng minh rằng nếu \(0^o< x< 90^o\) thì \(sin^6x+cos^6x+sin^6x.cos^6x\le80\)
(Định lý sin) Cho tam giác nhọn ABC có BC = a, AC = b, AB = c và nội tiếp đường tròn (O ; R). Chứng minh rằng:
$\dfrac{a}{\sin{A}}=\dfrac{b}{\sin{B}}=\dfrac{c}{\sin{C}}=2R$.
\(S_{ABC}=\frac{bc\sin A}{2}=\frac{ac\sin B}{2}=\frac{ab\sin C}{2}=\frac{abc}{4R}\)
+ Từ \(\frac{bc\sin A}{2}=\frac{ac\sin B}{2}\Rightarrow b\sin A=a\sin B\Rightarrow\frac{a}{\sin A}=\frac{b}{\sin B}\left(1\right)\)
+ Từ \(\frac{ac\sin B}{2}=\frac{ab\sin C}{2}\Rightarrow c\sin B=b\sin C\Rightarrow\frac{b}{\sin B}=\frac{c}{\sin C}\left(2\right)\)
+ Từ \(\frac{bc\sin A}{2}=\frac{abc}{4R}\Rightarrow\sin A=\frac{a}{2R}\Rightarrow\frac{a}{\sin A}=2R\left(3\right)\)
Từ (1) (2) (3) \(\Rightarrow\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\left(dpcm\right)\)
Từ A kẻ đường cao AH (H thuộc BC) , Từ B kẻ đường cao BK (K thuộc AC)
Ta có : ; ;
;
(1)
Lại có :
(2)
Từ (1) và (2) ta có : (Đpcm)
Kẻ đường kính BD.
ta có góc A = góc D ( góc nội tiếp chắn cung BC)
=> sinA = sin D
có tam giác BCD vuông tại C => sinD = BD/BC
=> sinA = 2R/a
=> a/sinA=2R
CMTT ta có b/sinB =2R
c/sinC=2R
do đó a/sinA=b/sinB=c/sinC=2R
Xem thêm câu trả lời
Cho \(0^o< x< 90^o\). Chứng minh: Giá trị biểu thức sau không phụ thuộc vào giá trị của biến: \(P=\sin^6x+\cos^6x+3\sin^2x.\cos^2x+\tan^2x.\cos^2x+\cot^2x.\sin^2x\)
\(=\left(sin^2x+cos^2x\right)^3-3sin^2x\cdot cos^2x\cdot\left(sin^2x+cos^2x\right)+3\cdot sin^2xcos^2x+sin^2x+cos^2x\)
\(=1+1=2\)
Đúng 0
Bình luận (0)
Cho biểu thức \(A=\dfrac{cos70^o-sin\alpha}{tan60^o-cos70^o}\)( 200 <\(\alpha\) < 900). Chứng minh A < 0
Sửa: \(A=\dfrac{\cos70^0-\sin\alpha}{\tan60^0-\cot70^0}\)
Vì \(\sin\alpha>\sin20^0\Leftrightarrow\cos70^0-\sin\alpha< \sin20^0-\sin20^0=0\)
Mà \(\tan60^0-\cot70^0=\tan60^0-\tan20^0>0\)
Do đó \(A< 0,\forall20^0< \alpha< 90^0\)
Đúng 2
Bình luận (0)
Chứng minh rằng với mọi góc \(\alpha \;\;({0^o} \le \alpha \le {180^o})\), ta đều có:
a) \({\cos ^2}\alpha + {\sin ^2}\alpha = 1\)
b) \(\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})\)
c) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})\)
d) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})\)
a)
Trên nửa đường tròn đơn vị, lấy điểm M sao cho \(\widehat {xOM} = \alpha \)
Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.
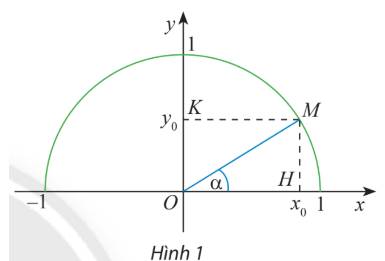
Ta có: tam giác vuông OHM vuông tại H và \(\alpha = \widehat {xOM}\)
Do đó: \(\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.\)
\( \Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1\)
b) Ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}\)
c) Với \(\alpha \ne {90^o}\) ta có:
\(\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}\)
d) Ta có:
\(\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}\)
Đúng 0
Bình luận (0)






















