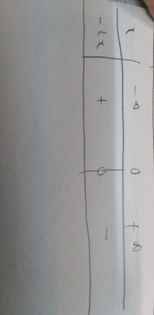
Xét dấu nhị thức f(x)=5-3x

Những câu hỏi liên quan
Xét dấu các nhị thức f(x) = 3x + 2, g(x) = -2x + 5.
Nhị thức 3x + 2 có nghiệm là: 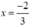 . Bảng xét dấu của f(x)= 3x + 2:
. Bảng xét dấu của f(x)= 3x + 2:

Nhị thức – 2x + 5 có nghiệm là: 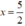 . Bảng xét dấu của g(x) = -2x + 5
. Bảng xét dấu của g(x) = -2x + 5

Đúng 0
Bình luận (0)
Lập bảng xét dấu nhị thức bậc nhất của:
a) f(x) = 3x-5
b) f(x) = 2x+4
c) f(x) = -x+1
d) f(x) = -2x
xét dấu các biểu thức sau:
a) f(x) =(2x-4)(3x+5)
Với \(x>2\) thì f(x) > 0.
Với \(x<\frac{-3}{5}\) thì f(x) > 0.
Với \(\frac{-3}{5}< x<2\) thì f(x) < 0.
Với x = 2 thì f(x) = 0.
Với \(x=\frac{-3}{5}\) thì f(x) = 0.
Đúng 1
Bình luận (0)
Xét dấu các tam thức:
a, \(f\left(x\right)=-x^2+3x-5\)
b, \(g\left(x\right)=-2x^2+3x+5\)
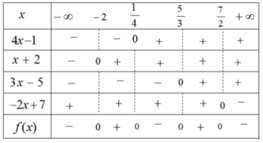
Xét dấu biểu thức sau: f(x) = (4x - 1)(x + 2)(3x - 5)(-2x + 7)
Xét dấu các biểu thức sau:
a) f(x)= (x-2).(x+1)/3x -1
b) f(x)= 1-4x /2x-3
c) f(x)= 3x (6 -2x)/5x-4
d) f(x)= -4/3x+1 - 3/2-x
e) f(x)= 2x-5/(3x+1) (2-4x)
Xem chi tiết
Xét các dấu nhị thức sau đây:h(x)=-x-3
Xem chi tiết
Lời giải:Với $x\in (-3;+\infty)$ thì $f(x)<0$
Với $x\in (-\infty; -3)$ thì $f(x)>0$
Với $x=-3$ thì $f(x)=0$
Đúng 0
Bình luận (0)
Xét dấu biểu thức: f(x) = (-3x - 3)(x + 2)(x + 3)
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
Ta có bảng xét dấu :

Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
Đúng 0
Bình luận (0)
giải bất phương trình : \(\frac{x+2}{3x+1}\)<= \(\frac{x-2}{2x-1}\)
giải bằng xét dấu nhị thức bậc nhất