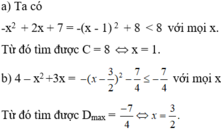giá trị lớn nhất của biểu thức A = 7 - (x2 + 1)2 là:

Những câu hỏi liên quan
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức:
a) A = x2-4x+20
b) B = x2+3x+7
c) C = -x2-10x+70
d) D = -4x2+12x+1
\(A=x^2-4x+20=x^2-4x+4+16=\left(x-2\right)^2+16\)
Do \(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2+16\ge16\)
\(\Rightarrow Min\left(A\right)=16\)
\(B=x^2-3x+7=x^2-3x+\dfrac{9}{4}-\dfrac{9}{4}+7=\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\)
Do \(\left(x-\dfrac{3}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
\(\Rightarrow Min\left(B\right)=\dfrac{19}{4}\)
\(C=-x^2-10x+70=-\left(x^2+10x+25\right)+25+70=-\left(x-5\right)^2+95\)
Do \(-\left(x-5\right)^2\le0\)
\(\Rightarrow-\left(x-5\right)^2+95\le95\)
\(\Rightarrow Max\left(C\right)=95\)
\(D=-4x^2+12x+1=-\left(4x^2-12x+9\right)+9+1=-\left(2x-3\right)^2+10\)
Do \(-\left(2x-3\right)^2\le0\)
\(\Rightarrow-\left(2x-3\right)^2+10\le10\)
\(\Rightarrow Max\left(D\right)=10\)
Đúng 3
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A,B,C và giá trị lớn nhất của biểu thức D,E:
A= x2-4x+1 D= 5-8x-x2
B= 4x2+4x+11 E= 4x-x2+1
C= (x-1).(x+3).(x+2).(x+6)
`A=x^2-4x+1`
`=x^2-4x+4-3`
`=(x-2)^2-3>=-3`
Dấu "=" xảy ra khi x=2
`B=4x^2+4x+11`
`=4x^2+4x+1+10`
`=(2x+1)^2+10>=10`
Dấu "=" xảy ra khi `x=-1/2`
`C=(x-1)(x+3)(x+2)(x+6)`
`=[(x-1)(x+6)][(x+3)(x+2)]`
`=(x^2+5x-6)(x^2+5x+6)`
`=(x^2+5x)^2-36>=-36`
Dấu "=" xảy ra khi `x=0\or\x=-5`
`D=5-8x-x^2`
`=21-16-8x-x^2`
`=21-(x^2+8x+16)`
`=21-(x+4)^2<=21`
Dấu "=" xảy ra khi `x=-4`
`E=4x-x^2+1`
`=5-4+4-x^2`
`=5-(x^2-4x+4)`
`=5-(x-2)^2<=5`
Dấu "=" xảy ra khi `x=5`
Đúng 3
Bình luận (0)
A= x2 - 4x +1
= x2 - 4x + 4 - 3
= (x-2)2 -3
Ta có (x-2)2 ≥ 0 ∀ x
⇒ (x-2)2 -3 ≥ -3 ∀ x
Vậy AMin= -3 tại x=2
B= 4x2+4x+11
= 4x2+4x+1+10
= (2x+1)2+10
Ta có (2x+1)2 ≥ 0 ∀ x
⇒ (2x+1)2+10 ≥ 10 ∀ x
Vậy BMin=10 tại x= \(\dfrac{-1}{2}\)
C=(x-1)(x+3)(x+2)(x+6)
= (x-1)(x+6)(x+3)(x+2)
= (x2+5x-6) (x2+5x+6)
= (x2+5x)2 -36
Ta có (x2+5x)2 ≥ 0 ∀ x
⇒ (x2+5x)2 -36 ≥ -36 ∀ x
Vậy CMin=-36 tại x=0 hoặc x= -5
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức A, B, C và giá trị lớn nhất của biểu thức D, E:
A = x2 – 4x + 1
B = 4x2 + 4x + 11
C = (x – 1)(x + 3)(x + 2)(x + 6)
D = 5 – 8x – x2
E = 4x – x2 +1
Tính giá trị nhỏ nhất:
\(A=x^2-4x+1=(x^2-4x+4)-3=(x-2)^2-3\)
Vì $(x-2)^2\geq 0, \forall x\in\mathbb{R}$ nên $A=(x-2)^2-3\geq 0-3=-3$
Vậy $A_{\min}=-3$
Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$
$B=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 0+10=10$
Vậy $B_{\min}=10$
Giá trị này đạt tại $(2x+1)^2=0\Leftrightarrow x=-\frac{1}{2}$
$C=(x-1)(x+3)(x+2)(x+6)$
$=(x-1)(x+6)(x+3)(x+2)$
$=(x^2+5x-6)(x^2+5x+6)$
$=(x^2+5x)^2-36\geq 0-36=-36$
Vậy $C_{\min}=-36$. Giá trị này đạt $x^2+5x=0\Leftrightarrow x=0$ hoặc $x=-5$
Đúng 3
Bình luận (0)
Tìm giá trị lớn nhất:
$D=5-8x-x^2=21-(x^2+8x+16)=21-(x+4)^2$
Vì $(x+4)^2\geq 0, \forall x\in\mathbb{R}$ nên $D=21-(x+4)^2\leq 21$
Vậy $D_{\max}=21$. Giá trị này đạt tại $(x+4)^2=0\Leftrightarrow x=-4$
$E=4x-x^2+1=5-(x^2-4x+4)=5-(x-2)^2\leq 5$
Vậy $E_{\max}=5$. Giá trị này đạt tại $(x-2)^2=0\Leftrightarrow x=2$
Đúng 2
Bình luận (0)
Tìm giá trị lớn nhất của biểu thức:
a) C = - x 2 +2x + 7; b) D = 4- x 2 +3x.
Câu 18: Giá trị nhỏ nhất của biểu thức x2 – 6x + 13 làA. 3 B. 4 C. -3 D. -4 Câu 19 : Giá trị lớn nhất của biểu thức -x2 +4x - 7 làA. 3 B. 4 C. -3 D. 5 Câu 20: Điền vào chỗ trống 4x2 + 4x – y2 + 1 (…)(2x + y + 1): A. 2x + y + 1 B. 2x – y + 1 C....
Đọc tiếp
Câu 18: Giá trị nhỏ nhất của biểu thức x2 – 6x + 13 là
A. 3 B. 4 C. -3 D. -4
Câu 19 : Giá trị lớn nhất của biểu thức -x2 +4x - 7 là
A. 3 B. 4 C. -3 D. 5
Câu 20: Điền vào chỗ trống 4x2 + 4x – y2 + 1 = (…)(2x + y + 1):
A. 2x + y + 1 B. 2x – y + 1
C. 2x – y D. 2x + y
Tìm giá trị lớn nhất của biểu thức A=x2/x4+x2+1
Bài 4. Tìm giá trị nhỏ nhất của các biểu thức:
a) A = 2x2 – 15 ; b) B = 2(x + 1)2 – 17.
Bài 5. Tìm giá trị lớn nhất của các biểu thức:
a) A = 14 – x2; b) B = 25 – (x – 2)2
mik sẽ tick nha
Bài 4:
\(A=2x^2-15\ge-15\\ A_{min}=-15\Leftrightarrow x=0\\ B=2\left(x+1\right)^2-17\ge-17\\ B_{min}=-17\Leftrightarrow x=-1\)
Bài 5:
\(A=-x^2+14\le14\\ A_{max}=14\Leftrightarrow x=0\\ B=25-\left(x-2\right)^2\le25\\ B_{max}=25\Leftrightarrow x=2\)
Đúng 2
Bình luận (1)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: A= 6x+8/x2+1
A+1 = x^2+6x+9/x^2+1 = (x+3)^2/x^2+1 >= 0
=> A >= -1
Dấu "=" xảy ra <=> x+3=0 <=> x=-3
Vậy GTNN của A = -1 <=> x=-3
Tk mk nha
Đúng 0
Bình luận (0)
câu 1: giá trị nhỏ nhất của biểu thức |2.x -13|-7/4 là.....
câu 2: giá trị nhỏ nhất của biểu thức |1-3.x| cộng 1 là......
câu 3: giá trị lớn nhất của biểu thức q=3.|1-2.x|-5 là.....
câu 4:giá trị nguyên nhỏ nhất của n để biểu thức A= \(\frac{3n+9}{n-4}\) có giá trị là 1 số nguyên là......
Bài 1: Tìm giá trị nhỏ nhất của các biểu thứca ) A x2 – 2x+5b) B x2 –x +1c) C ( x -1). ( x +2). ( x+3). ( x+6)d) D x2 + 5y2 – 2xy+ 4y+3Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:a) A -x2 – 4x – 2 b) B -2x2 – 3x +5c) C ( 2- x). ( x +4)d) D -8x2 + 4xy - y2 +3Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biếna) A 25x – 20x+7b) B 9x2 – 6xy + 2y2 +1c) E x2 – 2x + y2 + 4y+6d) D x2 – 2x +2Giúp mình nha. Cần gấp ạ Chi tiết nha
Đọc tiếp
Bài 1: Tìm giá trị nhỏ nhất của các biểu thức
a ) A= x2 – 2x+5
b) B= x2 –x +1
c) C= ( x -1). ( x +2). ( x+3). ( x+6)
d) D= x2 + 5y2 – 2xy+ 4y+3
Bài 2: Tìm giá trị lớn nhất của các biểu thức sau:
a) A= -x2 – 4x – 2
b) B= -2x2 – 3x +5
c) C= ( 2- x). ( x +4)
d) D= -8x2 + 4xy - y2 +3
Bài 3 : Chứng minh rằng các giá trị của các biểu thức sau luôn dương với mọi giá trị của biến
a) A= 25x – 20x+7
b) B= 9x2 – 6xy + 2y2 +1
c) E= x2 – 2x + y2 + 4y+6
d) D= x2 – 2x +2
Giúp mình nha. Cần gấp ạ <Chi tiết nha>
Bài 3:
a) Ta có: \(A=25x^2-20x+7\)
\(=\left(5x\right)^2-2\cdot5x\cdot2+4+3\)
\(=\left(5x-2\right)^2+3>0\forall x\)(đpcm)
d) Ta có: \(D=x^2-2x+2\)
\(=x^2-2x+1+1\)
\(=\left(x-1\right)^2+1>0\forall x\)(đpcm)
Đúng 0
Bình luận (0)
Bài 1:
a) Ta có: \(A=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)