Cho ΔABC có AB>AC. D là trung điểm của BC. Lấy E∈AB, F∈AC: BE=CF. So sánh ∠DEF ; ∠DFE

Những câu hỏi liên quan
Bài 12: Cho tam giác ABC có D, E, F lần lượt là trung điểm của BC, CA, AB. Trên tia đối của tia
DA lấy I sao cho D là trung điểm của AI.
a) So sánh AB và CI.
b) Chứng minh: AB+ AC > 2.AD
c) Chứng minh: AB + AC + BC > AD+ BE + CF
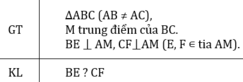
Cho ΔABC (AB ≠ AC) tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E, F thuộc Ax). So sánh các độ dài BE và CF.
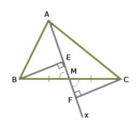
Hai tam giác vuông BME và CMF có
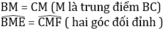
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???
Đúng 0
Bình luận (0)
Cho ΔABC vuông tại A, có AB = 9cm, BC = 15 cm, AC=12 cm.
a) so sánh các góc của ΔABC
b) trên tia đối của AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Chừng minh ΔABC = ΔADC
c) E là trung điểm cạnh CD,BE cắt AC ở I. Chứng minh DI đi qua trung điểm cạnh BC
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xet ΔABC có
BC^2=AB^2+AC^2
=>ΔBCA vuông tại A
Xet ΔCAB vuông tại A và ΔCAD vuông tại A có
CA chung
AB=AD
=>ΔCAB=ΔCAD
c: Xét ΔCBD có
CA,BE là trung tuyến
CA cắt BE tại I
=>I là trọng tâm
=>DI đi qua trung điểm của BC
Đúng 1
Bình luận (0)
Cho ΔABC vuông tại A, có AB = 8cm, AC = 6cm. Trên cạnh BC lấy điểm D sao cho BA = BD. Từ D kẻ đường thẳng vuông góc với BC, đường thẳng này cắt AC tại E
a) Tính độ dài canh BC?
b) Chứng minh ΔABE = ΔDBE
c) Gọi F là giao điểm của tia DE và tia BA. So sánh BF và BC
d) Chứng minh BE là trung trực của đoạn thẳng CF
a, áp dụng định lí py-ta-go ta có:
\(AB^2+AC^2=BC^2\)
=>\(BC^2\)=64+36=100(cm)
=>BC=10cm
vậy BC=10cm
b,xét 2t.giác vuông ABE và DBE có:
EB chung
AB=BD(gt)
=>t.giác ABE=t.giác DBE(cạnh huyền-cạnh góc vuông)
c,xét 2 t.giác vuông AEF và t.giác DEC có:
AE=DE(theo câu b)
\(\widehat{AEF}\)=\(\widehat{DEC}\)(vì đối đỉnh)
=>t.giác AEF=t.giác DEC(cạnh góc vuông-góc nhọn)
=>AF=DC mà BA=BD(gt) suy ra BF=BC
d,gọi O là giao điểm của BE và CF
xét t.giác BFO và t.giác BCO có:
BF=BC(theo câu c)
\(\widehat{FBO}\)=\(\widehat{CBO}\)(theo câu b)
BO cạnh chung
=> t.giác BFO=t.giác BCO(c.g.c)
=>CO=OF =>O là trung điểm của CF(1); \(\widehat{COB}\)=\(\widehat{FOB}\)mà 2 góc này ở vị trí kề bù nên \(\widehat{COB}\)=\(\widehat{FOB}\)=90 độ =>BO\(\perp\)CF(2)
Từ (1) và (2) suy ra BE là trung trực của CF
học tốt!
Đúng 0
Bình luận (0)
Cho ΔABC có AB = AC, tia phân giác của góc BAC cắt BC tại D.
1) Chứng minh rằng: AD ⊥ BC .
2) Lấy điểm E thuộc AB, điểm F thuộc AC, sao cho BE = CF. Chứng minh DA là tia phân giác của góc EDF.
1: Xét ΔADB và ΔADC có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔADB=ΔADC
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
2: Ta có: AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
Xét ΔEAD và ΔFAD có
AE=AF
\(\widehat{EAD}=\widehat{FAD}\)
AD chung
Do đó: ΔEAD=ΔFAD
=>\(\widehat{EDA}=\widehat{FDA}\)
=>DA là phân giác của góc EDF
Đúng 2
Bình luận (0)
Lời giải:
1. Xét tam giác $ABD$ và $ACD$ có:
$AB=AC$
$\widehat{BAD}=\widehat{CAD}$ (do $AD$ là tia phân giác $\widehat{BAC}$)
$AD$ chung
$\Rightarrow \triangle BAD=\triangle CAD$ (c.g.c)
$\Rightarrow \widehat{ADB}=\widehat{ADC}$
Mà $\widehat{ADB}+\widehat{ADC}=180^0$
$\Rightarrow \widehat{ADB}=\widehat{ADC}=180^0:2=90^0$
$\Rightarrow AD\perp BC$
2.
$AB=AC$
$BE=CF$
$\Rightarrow AB-BE=AC-CF$ hay $AE=AF$
Xét tam giác $AED$ và $AFD$ có:
$AD$ chung
$AE=AF$
$\widehat{EAD}=\widehat{FAD}$
$\Rightarrow \triangle AED=\triangle AFD$ (c.g.c)
$\Rightarrow \widehat{EDA}=\widehat{FDA}$
$\Rightarrow DA$ là tia phân giác $\widehat{EDF}$
Đúng 2
Bình luận (0)
cho ΔABC (AB \(\ne\) AC) tia Ax đi qa trung điểm M của BC. Kẻ BE và CF vuông góc vs Ax ( E thuôc Ax, F thuộc Ax). So sánh độ dài BE và CF
Ta có hình vẽ trên:
Xét 2 tam giác vuông MBE và tam giác MCF có:
BM = MC (gt)
góc M1 = góc M2 (đối đỉnh)
suy ra tam giác MBE = tam giác MCF (cạnh huyền - góc nhọn)
suy ra BE = CF (2 cạnh tương ứng)
Vậy BE = CF
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC), có AM là trung tuyến (M thuộc BC). Trên tia đối của tia MA lấy điểm E sao cho ME = MA, nối B với E.
a) Chứng minh rằng: BE = AC và BE // AC.
b) Gọi D là trung điểm của AB. Trên tia đối của tia DE lấy điểm F sao cho DF = DE. Chứng minh rằng A là trung điểm của CF.
c) So sánh độ lớn hai góc BAM và MAC
ΔABC(AB≠AC),tia Ax qua trung điểm M của BC. BE và CF ⊥Ax. So sánh BE và CF
Xét ΔBME vuông tại E và ΔCMF vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBME=ΔCMF
Suy ra: BE=CF
Đúng 0
Bình luận (0)
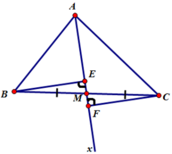
Cho ΔABC ( AB<AC). O là trung điểm của BC. Kẻ BE và CF cùng ⊥ với OA. (E, F ∈ OA )
a. CM: OE = OF
b. CM: CE // BF
c. Lấy M nằm giữa B và F, N ∈ CE sao cho BM = CN. CM: O là trung điểm của MN