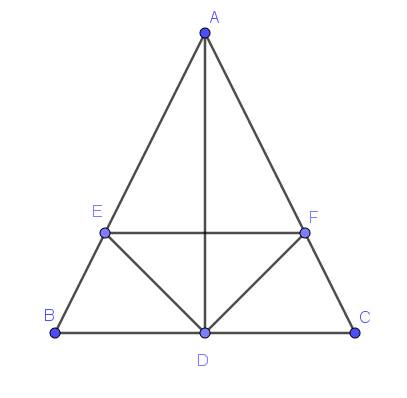
1: Xét ΔADB và ΔADC có
AB=AC
\(\widehat{BAD}=\widehat{CAD}\)
AD chung
Do đó: ΔADB=ΔADC
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
2: Ta có: AE+EB=AB
AF+FC=AC
mà EB=FC và AB=AC
nên AE=AF
Xét ΔEAD và ΔFAD có
AE=AF
\(\widehat{EAD}=\widehat{FAD}\)
AD chung
Do đó: ΔEAD=ΔFAD
=>\(\widehat{EDA}=\widehat{FDA}\)
=>DA là phân giác của góc EDF
Lời giải:
1. Xét tam giác $ABD$ và $ACD$ có:
$AB=AC$
$\widehat{BAD}=\widehat{CAD}$ (do $AD$ là tia phân giác $\widehat{BAC}$)
$AD$ chung
$\Rightarrow \triangle BAD=\triangle CAD$ (c.g.c)
$\Rightarrow \widehat{ADB}=\widehat{ADC}$
Mà $\widehat{ADB}+\widehat{ADC}=180^0$
$\Rightarrow \widehat{ADB}=\widehat{ADC}=180^0:2=90^0$
$\Rightarrow AD\perp BC$
2.
$AB=AC$
$BE=CF$
$\Rightarrow AB-BE=AC-CF$ hay $AE=AF$
Xét tam giác $AED$ và $AFD$ có:
$AD$ chung
$AE=AF$
$\widehat{EAD}=\widehat{FAD}$
$\Rightarrow \triangle AED=\triangle AFD$ (c.g.c)
$\Rightarrow \widehat{EDA}=\widehat{FDA}$
$\Rightarrow DA$ là tia phân giác $\widehat{EDF}$