Hai tam giác vuông BME và CMF có
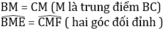
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???


Hai tam giác vuông BME và CMF có
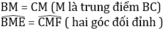
⇒ ΔBME = ΔCMF (cạnh huyền – góc nhọn)
⇒ BE = CF (hai cạnh tương ứng).
* Chú ý: Các em có thể suy nghĩ tại sao cần điều kiện AB ≠ AC ???
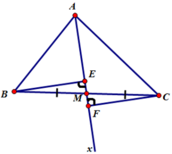
Cho tam giác ABC (AB khác AC) tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax,F thuộc Ax) so sánh các độ dài BE và CF
Cho ΔABC (AB khác AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E; F ϵ Ax). So sáh độ dài BE và CF.
Cho tam giác ABC (AB#AC) ,tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax;F thuộc Ax). so sánh các độ dà BE và CF.
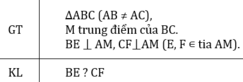
Cho tam giác ABC (AB ≠ AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax, F thuộc Ax).
a) So sánh độ dài BE và CF;
b) Chứng minh rằng EC // BF.
Cho tam giác ABC (AB khác AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax ( E , F thuộc Ax) . So sánh độ dài BE và CF.
Vẽ hình và nêu giả thiết kết luận của bài nài nhé
cho tam giác ABC(AB €AC)tia Ax đi qua trung điểm M của BC.Kẻ BE và CF vuông góc vớiAx (E thuộc à ,F thuộc Ax)so sánh các độ dài BE vàCF
Cho tam giác ABC (AB≠AC), tia Ax đi qua trung điểm MM của BC.
Kẻ BE và CF vuông góc với Ax (E ∈ Ax ,F ∈ Ax) . So sánh độ dài BE và CF
Cho tam giác ABC ( AB>AC) , tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuôn góc với Ax( E thuộc Ax F thuộc Ax . Chứng minh a) BE=CF b)BF=CE
Cho tam giác ABC AB khác AC, tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E,F thuộc Ax).
a) Chứng minh: BE//CP.
b) So sánh BE và FC; CE và BF.
c) Tìm điều kiện về tam giác ABC để có BE = CE.