Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBEM=ΔCFM
Xét ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
\(\widehat{BME}=\widehat{CMF}\)
Do đó: ΔBEM=ΔCFM
Cho tam giác ABC (AB khác AC) tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax,F thuộc Ax) so sánh các độ dài BE và CF
Cho tam giác ABC (AB ≠ AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax, F thuộc Ax).
a) So sánh độ dài BE và CF;
b) Chứng minh rằng EC // BF.
Cho tam giác ABC (AB#AC) ,tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E thuộc Ax;F thuộc Ax). so sánh các độ dà BE và CF.
Cho ΔABC (AB ≠ AC) tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E, F thuộc Ax). So sánh các độ dài BE và CF.
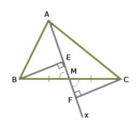
Cho tam giác ABC AB khác AC, tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E,F thuộc Ax).
a) Chứng minh: BE//CP.
b) So sánh BE và FC; CE và BF.
c) Tìm điều kiện về tam giác ABC để có BE = CE.
cho tam giác ABC(AB €AC)tia Ax đi qua trung điểm M của BC.Kẻ BE và CF vuông góc vớiAx (E thuộc à ,F thuộc Ax)so sánh các độ dài BE vàCF
Cho ΔABC (AB khác AC), tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuông góc với Ax (E; F ϵ Ax). So sáh độ dài BE và CF.
Cho tam giác ABC (AB≠AC), tia Ax đi qua trung điểm MM của BC.
Kẻ BE và CF vuông góc với Ax (E ∈ Ax ,F ∈ Ax) . So sánh độ dài BE và CF
Cho tam giác ABC ( AB>AC) , tia Ax đi qua trung điểm M của BC. Kẻ BE và CF vuôn góc với Ax( E thuộc Ax F thuộc Ax . Chứng minh a) BE=CF b)BF=CE