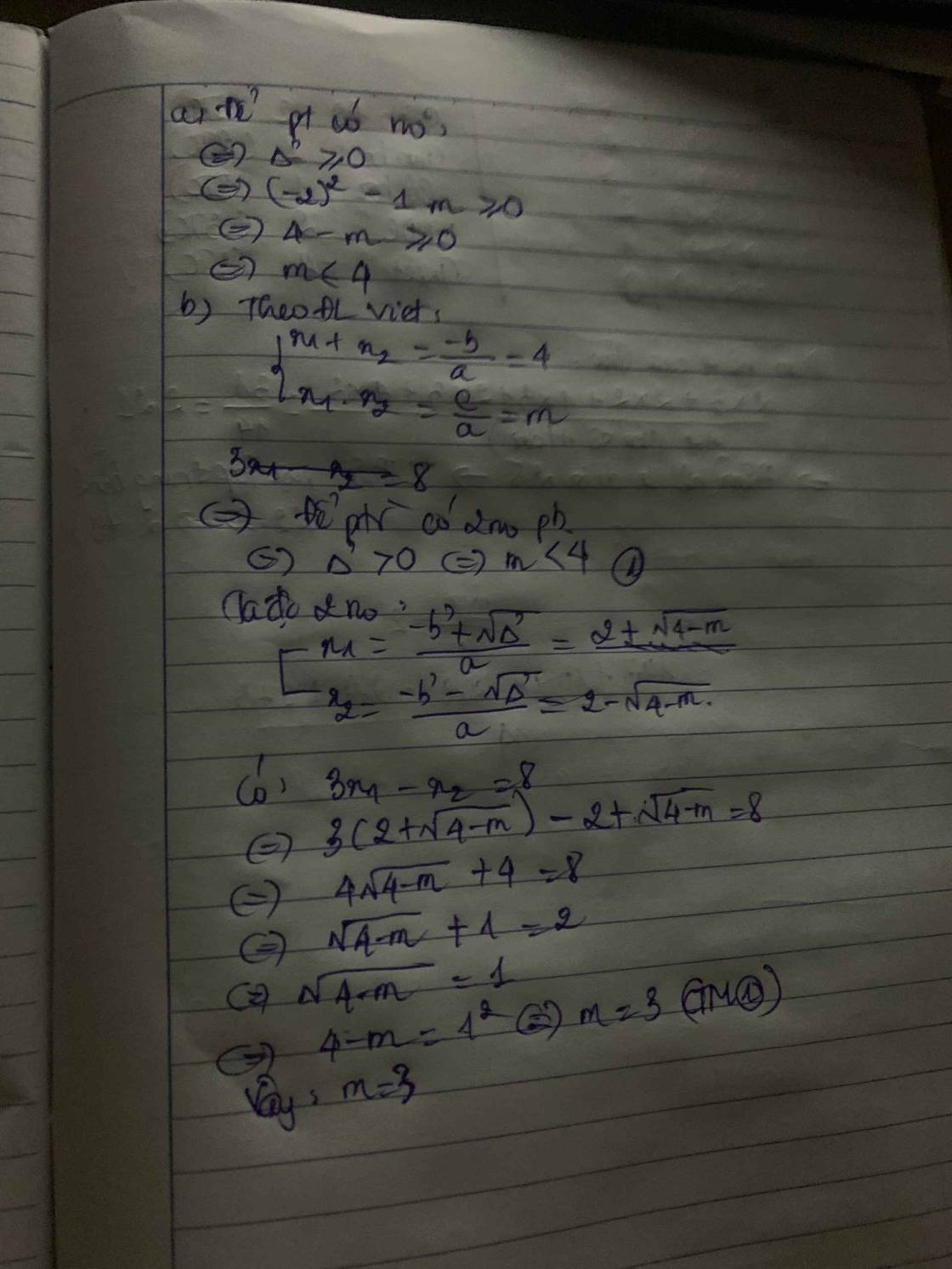Đáp án D

2 sin 2 x + m sin 2 x = 2 m ⇔ 1 − cos 2 x + m sin 2 x = 2 m ⇔ m sin 2 x − cos 2 x = 2 m − 1

Để phương trình vô nghiệm 

⇔ 2 m − 1 2 > m 2 + 1

⇔ 3 m 2 − 4 m > 0 ⇔ m ∈ − ∞ ; 0 ∪ 4 3 ; + ∞

a) Thay m=3 vào pt ta được:

\(9x+6=4x+9\Leftrightarrow x=\dfrac{3}{5}\)

Vậy...

b) Thay x=-1,5 vào pt ta được:

\(m^2\left(-1,5\right)+6=4.\left(-1,5\right)+3m\)

\(\Leftrightarrow\dfrac{-3}{2}m^2-3m+12=0\)\(\Leftrightarrow\left[{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)

Vậy...

c)Pt \(\Leftrightarrow x\left(m^2-4\right)=3m-6\)

Để pt vô nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}3m-6\ne0\\m^2-4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\ne2\\m=\pm2\end{matrix}\right.\)\(\Rightarrow m=-2\)

Để pt có vô số nghiệm \(\Leftrightarrow\left\{{}\begin{matrix}3m-6=0\\m^2-4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=\pm2\end{matrix}\right.\)\(\Rightarrow m=2\)

d)Để pt có nghiệm \(\Leftrightarrow m^2-4\ne0\Leftrightarrow m\ne\pm2\)

 \(\Rightarrow x=\dfrac{3m-6}{m^2-4}=\dfrac{3\left(m-2\right)}{\left(m-2\right)\left(m+2\right)}=\dfrac{3}{m+2}\)

Để \(x\in Z\Leftrightarrow\dfrac{3}{m+2}\in Z\)

Vì \(m\in Z\Leftrightarrow m+2\in Z\).Để \(\dfrac{3}{m+2}\in Z\Leftrightarrow m+2\inƯ\left(3\right)=\left\{-1;-3;1;3\right\}\)

\(\Leftrightarrow m=\left\{-3;-5;-1;1\right\}\) (tm)

Vậy...

\(x^4+2x^3+5x^2+4x-1-m=0\)

\(\Leftrightarrow\left(x^2+x\right)^2+4\left(x^2+x\right)-1-m=0\left(1\right)\)

\(đặt:x^2+x=t\ge\dfrac{-\Delta}{4a}=-\dfrac{1}{4}\)

\(\left(1\right)\Leftrightarrow t^2+4t-1-m=0\) có nghiệm trên \([-\dfrac{1}{4};\text{+∞})\)

\(f\left(t\right)=t^2+4t-1=m\)

\(f\left(-\dfrac{b}{2a}\right)=-5\)

\(f\left(-\dfrac{1}{4}\right)=-\dfrac{31}{16}\Rightarrow m\ge-\dfrac{31}{16}\Rightarrow\left[{}\begin{matrix}t=\dfrac{-b}{2a}=-2\Rightarrow x^2+x+2=0\left(vô-nghiệm\right)\left(loại\right)\\\left\{{}\begin{matrix}t1=\dfrac{-4+\sqrt{20+4m}}{2}=-2+\sqrt{5+m}\\t2=\dfrac{-4-\sqrt{20+4m}}{2}=-2-\sqrt{5+m}\end{matrix}\right.\end{matrix}\right.\) 

\(x^2+x=t1=-2+\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=\sqrt{5+m}\) có nghiệm thuộc \(\left[-1;1\right]\)

\(\Rightarrow f\left(-\dfrac{b}{2a}\right)=\dfrac{7}{4}\)

\(f\left(-1\right)=2;f\left(1\right)=4\)

\(\Rightarrow\dfrac{7}{4}\le\sqrt{5+m}\le4\Leftrightarrow\dfrac{-31}{16}\le m\le11\)

\(x^2+x=t2=-2-\sqrt{5+m}\Leftrightarrow f\left(x\right)=x^2+x+2=-\sqrt{5+m}\)

có nghiệm trên \(\left[-1;1\right]\)

\(x^2+x+2>0\Rightarrow x^2+x+2=-\sqrt{5+m}< 0\left(vô-lí\right)\Rightarrow vô-nghiệm\forall m\)

\(\Rightarrow\dfrac{-31}{16}\le m\le11\) thì pt có  nghiệm thuộc \(\left[-1;1\right]\)

\(\Leftrightarrow\dfrac{m}{2}\left(1-cos4x\right)-\dfrac{3}{2}sin4x+\dfrac{1+cos4x}{2}=2\)

\(\Leftrightarrow\left(1-m\right)cos4x-3sin4x=3-m\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất, pt đã cho có nghiệm khi:

\(\left(1-m\right)^2+\left(-3\right)^2\ge\left(3-m\right)^2\)

\(\Leftrightarrow4m+1\ge0\Leftrightarrow m\ge-\dfrac{1}{4}\)