tìm m để pt có 3 nghiệm phân biệt lập thành 1 cấp số công:
x^3-6x^2+(m^2+2)x-m-3=0
Tìm m để pt có 3 nghiệm phân biệt lập thành 1 cấp số cộnga, \(x^3-3mx^2+2m\left(m-4\right)x+9m^2-m=0\)
b, \(\left(m-3\right)x^3+18x^2+72x+m^3-4m=0\)
1.
Do 3 nghiệm lập thành cấp số cộng \(\Rightarrow2x_2=x_1+x_3\)
Mà \(x_1+x_2+x_3=3m\)
\(\Rightarrow3x_2=3m\Rightarrow x_2=m\)
Thay lại pt ban đầu:
\(m^3-3m^3+2m\left(m-4\right)m+9m^2-m=0\)
\(\Leftrightarrow m^2-m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=1\end{matrix}\right.\)
- Với \(m=0\Rightarrow x^3=0\Rightarrow\) pt có đúng 1 nghiệm (ktm)
- Với \(m=1\Rightarrow x^3-3x^2-6x+8=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=1\\x=4\end{matrix}\right.\) (thỏa mãn)
Vậy \(m=1\)
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 1 nghiệm phân biệt
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 2 nghiệm phân biệt
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 3 nghiệm phân biệt
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
Bài 1: Tìm m để phương trình sau có 3 nghiệm lập thành 1 cấp số cộng:
1, \(x^3-x^2-m^2x+m^2=0\)
2, \((x-2)(x^2-2mx+2m+3)=0\)
3, \(x^3-(2m-3)x^2-mx+m-2=0\)
4, \(x^3+(2m-1)x^2+(4m+1)x+2m+3=0\)
Bài 2: Tìm m để phương trình sau có 4 nghiệm lập thành 1 cấp số cộng:
a, \(-x^4+2mx^2-2m+1=0\)
b, \(x^4+2(m-2)x^2+m^2-5m+5=0\)
Bài 3: Tìm 3 số lập thành 1 cấp số cộng biết tổng của chúng bằng tổng các bình phương bằng 83
Cho pt : x^-6x+m-3=0. Tìm m để pt có 2 nghiệm phân biệt thoả mãn: (x1-1)*(x2^-5x2+m-4)=0
(x1-1)(x2^2-5x2+m-4)=0
=>x1=1 và x2^2-x2(x1+x2-1)+x1x2+1=0
=>x1=1 và x2^2-x2x1-x2^2+x2+x1x2+1=0
=>x1=1 và x2=-1
x1*x2=m-3
=>m-3=-1
=>m=2
Tìm m để phương trình: x 3 − 3 x 2 + mx + 2 − m = 0 có 3 nghiệm phân biệt lập thành 1 cấp số cộng:
A. m ∈ − 3 ; + ∞ .
B. m ∈ ℝ .
C. m = 3
D. m ∈ − ∞ ; 3 .
Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
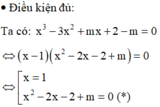
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
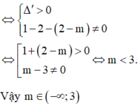
: x^2 – 2( m- 1)x – 4m = 0 ( 3)
⦁ Tìm m để PT(3) có nghiệm
⦁ Tìm m để PT(3) có 2 nghiệm phân biệt
help voi mn
*, Để pt (3) có nghiệm
\(\Delta'=\left(m-1\right)^2-\left(-4m\right)=m^2+2m+1=\left(m+1\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm x1 ; x2
*, \(\Delta'=\left(m+1\right)^2\ge0\)
Để pt có 2 nghiệm pb khi \(m+1\ne0\Leftrightarrow m\ne-1\)
Vậy với m khác -1 thì pt (3) luôn có 2 nghiệm pb
tìm m để pt có 3 nghiệm pb : \(4x^3-6x^2+m=0\)
tìm m ? thì y=\(\dfrac{x-3}{x+1}\) cắt y=x+m tại 2 điểm phân biệt
m? thì y=\(\dfrac{x+1}{x-1}\), y=-2x+m cắt tại 2 điểm phân biệt
1.
\(4x^3-6x^2+m=0\Leftrightarrow4x^3-6x^2=-m\)
Xét hàm \(f\left(x\right)=4x^3-6x^2\)
\(f'\left(x\right)=12x^2-12x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
BBT:
Từ BBT ta thấy đường thẳng \(y=-m\) cắt \(y=4x^3-6x^2\) tại 3 điểm pb khi:
\(-2< -m< 0\Leftrightarrow0< m< 2\)
2.
Pt hoành độ giao điểm:
\(\dfrac{x-3}{x+1}=x+m\)
\(\Rightarrow x-3=\left(x+m\right)\left(x+1\right)\)
\(\Leftrightarrow x^2+mx+m+3=0\) (1)
Đường thẳng cắt đồ thị tại 2 điểm pb khi và chỉ khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=m^2-4\left(m+3\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}m>6\\m< -2\end{matrix}\right.\)
3.
Pt hoành độ giao điểm:
\(\dfrac{x+1}{x-1}=-2x+m\)
\(\Leftrightarrow x+1=\left(x-1\right)\left(-2x+m\right)\)
\(\Leftrightarrow2x^2-\left(m+1\right)x+m+1=0\) (1)
bài toán thỏa mãn khi (1) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+1\right)^2-8\left(m+1\right)>0\)
\(\Leftrightarrow\left(m+1\right)\left(m-7\right)>0\)
\(\Rightarrow\left[{}\begin{matrix}m>7\\m< -1\end{matrix}\right.\)
Tìm m để phương trình \(x^4-2\left(m+1\right)x^2+2m+1=0\) có 4 nghiệm phân biệt lập thành 1 cấp số cộng
Bài 1 cho pt x^2-2(m+1)x+4m+m^2=0 .Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 sao cho biểu thức A =|x1-x2| đạt giá trị nhỏ nhất
bài 2 cho pt x^2+mx+2m-4=0.Tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+|x2|=3
bài 3 cho pt x^2-3x-m^2+1=0.tìm m để phương trình có 2 nghiệm phân biệt x1,x2 thỏa mãn |x1|+2|x2|=3