a. \(\dfrac{\sqrt{2}.\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{7}.\left(\sqrt{3}+\sqrt{5}\right)}=\dfrac{\sqrt{2}}{\sqrt{7}}=\sqrt{\dfrac{2}{7}}\)

d. \(\dfrac{\sqrt{6-2\sqrt{5}}}{\sqrt{5}-1}=\dfrac{\sqrt{5-2\sqrt{5}+1}}{\sqrt{5}-1}=\dfrac{\left(\sqrt{5}-1\right)^2}{\sqrt{5}-1}=\sqrt{5}-1\)

\(\sqrt{3-2\sqrt{2}}\)

d: \(D=\dfrac{2}{x^2-y^2}\cdot\sqrt{\dfrac{9\left(x^2+2xy+y^2\right)}{4}}\)

\(=\dfrac{2}{\left(x-y\right)\left(x+y\right)}\cdot\dfrac{3\left(x+y\right)}{2}\)

\(=\dfrac{3}{x-y}\)

Câu 1:

a: \(\dfrac{2}{5}\sqrt{75}-0,5\cdot\sqrt{48}+\sqrt{300}-\dfrac{2}{3}\cdot\sqrt{12}\)

\(=\dfrac{2}{5}\cdot5\sqrt{3}-0,5\cdot4\sqrt{3}+10\sqrt{3}-\dfrac{2}{3}\cdot2\sqrt{3}\)

\(=2\sqrt{3}-2\sqrt{3}+10\sqrt{3}-\dfrac{4}{3}\sqrt{3}\)

\(=10\sqrt{3}-\dfrac{4}{3}\sqrt{3}=\dfrac{26}{3}\sqrt{3}\)

b: \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}+\dfrac{3}{3+\sqrt{6}}\)

\(=\dfrac{\sqrt{3}\cdot3\sqrt{3}-2\sqrt{3}}{\sqrt{2}\left(3\sqrt{3}-2\right)}+\dfrac{3\left(3-\sqrt{6}\right)}{9-6}\)

\(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}+3-\sqrt{6}\)

\(=\dfrac{\sqrt{3}}{\sqrt{2}}+3-\sqrt{6}=3-\dfrac{\sqrt{6}}{2}\)

c: \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)

=\(\sqrt{9-2\cdot3\cdot\sqrt{6}+6}+\sqrt{24-2\cdot2\sqrt{6}\cdot3+9}\)

\(=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)

\(=\left|3-\sqrt{6}\right|+\left|2\sqrt{6}-3\right|\)

\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)

Bài 2:

a: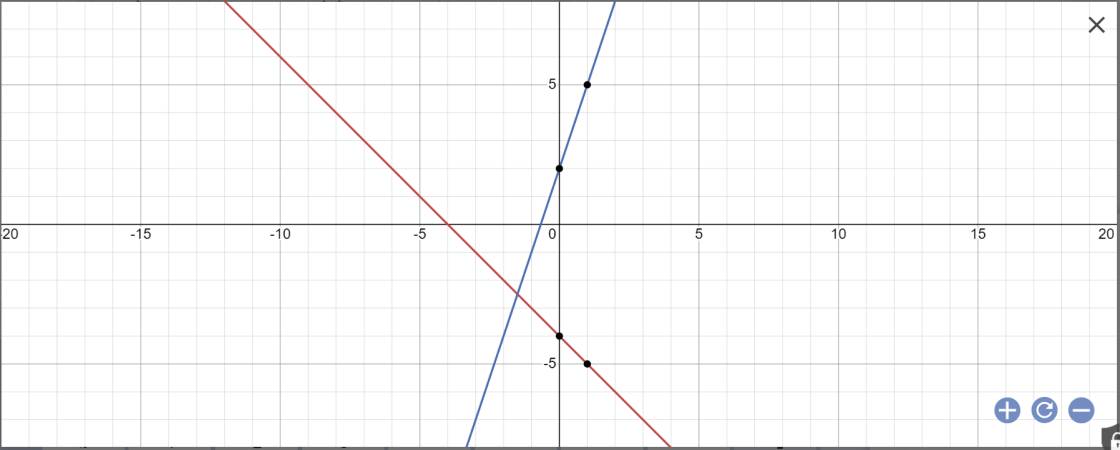 

b: Phương trình hoành độ giao điểm là:

\(3x+2=-x-4\)

=>4x=-6

=>x=-3/2

Thay x=-3/2 vào y=-x-4, ta được:

\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=-\dfrac{5}{2}\)

Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)

c: Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=-1\\b\ne-4\end{matrix}\right.\)

Vậy: (d2): y=-x+b

Thay x=-2 và y=5 vào (d2), ta được:

\(b-\left(-2\right)=5\)

=>b+2=5

=>b=5-2=3

Vậy: (d2): y=-x+3

a: \(\sqrt{15-6\sqrt{6}}+\sqrt{33-12\sqrt{6}}\)

\(=\sqrt{9-2\cdot3\cdot\sqrt{6}+6}+\sqrt{24-2\cdot2\sqrt{6}\cdot3+9}\)

\(=\sqrt{\left(3-\sqrt{6}\right)^2}+\sqrt{\left(2\sqrt{6}-3\right)^2}\)

\(=3-\sqrt{6}+2\sqrt{6}-3=\sqrt{6}\)

b: \(\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)

\(=\sqrt{\left(3+\sqrt{5}\right)^2}+\sqrt{\left(3-\sqrt{5}\right)^2}\)

\(=\left|3+\sqrt{5}\right|+\left|3-\sqrt{5}\right|\)

\(=3+\sqrt{5}+3-\sqrt{5}=6\)

c: \(\dfrac{3}{2\sqrt{3}+3}+\dfrac{3}{2\sqrt{3}-3}\)

\(=\dfrac{3\left(2\sqrt{3}-3\right)+3\left(2\sqrt{3}+3\right)}{12-9}\)

\(=2\sqrt{3}-3+2\sqrt{3}+3=4\sqrt{3}\)

d: \(\sqrt{\left(\sqrt{3}+4\right)\cdot\sqrt{19-8\sqrt{3}}+3}\)

\(=\sqrt{\left(4+\sqrt{3}\right)\cdot\sqrt{\left(4-\sqrt{3}\right)^2}+3}\)

\(=\sqrt{\left(4+\sqrt{3}\right)\cdot\left(4-\sqrt{3}\right)+3}\)

\(=\sqrt{16-3+3}=\sqrt{16}=4\)

e: \(\dfrac{9-2\sqrt{3}}{3\sqrt{6}-2\sqrt{2}}+\dfrac{3}{3+\sqrt{6}}\)

\(=\dfrac{\sqrt{3}\left(3\sqrt{3}-2\right)}{\sqrt{2}\left(3\sqrt{3}-2\right)}+\dfrac{3\left(3-\sqrt{6}\right)}{3}\)

\(=\dfrac{\sqrt{6}}{2}+3-\sqrt{6}=3-\dfrac{\sqrt{6}}{2}\)

\(\dfrac{\sqrt{6}+\sqrt{14}}{2\sqrt{3}+\sqrt{28}}\)

\(=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{2\sqrt{3}+2\sqrt{7}}\)

\(=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{2\left(\sqrt{3}+\sqrt{7}\right)}\)

\(=\dfrac{\sqrt{2}}{2}\)

___________

\(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{6}+\sqrt{8}+\sqrt{4}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)+\sqrt{2}\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)\left(1+\sqrt{2}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=1+\sqrt{2}\)

__________

\(\dfrac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\)

\(=\dfrac{3\cdot2\sqrt{2}-2\cdot2\sqrt{3}+2\sqrt{5}}{3\cdot3\sqrt{2}-2\cdot3\sqrt{3}+3\sqrt{5}}\)

\(=\dfrac{6\sqrt{2}-4\sqrt{3}+2\sqrt{5}}{9\sqrt{2}-6\sqrt{3}+3\sqrt{5}}\)

\(=\dfrac{2\left(3\sqrt{2}-2\sqrt{3}+\sqrt{5}\right)}{3\left(3\sqrt{2}-2\sqrt{3}+\sqrt{5}\right)}\)

\(=\dfrac{2}{3}\)

a: \(=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{2\left(\sqrt{3}+\sqrt{7}\right)}=\dfrac{\sqrt{2}}{2}\)

b: \(=\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{4}+\sqrt{4}+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\left(\sqrt{2}+\sqrt{3}+2\right)\left(1+\sqrt{2}\right)}{\sqrt{2}+\sqrt{3}+2}=1+\sqrt{2}\)

c: \(=\dfrac{6\sqrt{2}-4\sqrt{3}+2\sqrt{5}}{9\sqrt{2}-6\sqrt{3}+3\sqrt{5}}=\dfrac{2}{3}\)

\(\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-\left(\dfrac{\sqrt{3}-1}{4}\right)^2}=\dfrac{\sqrt{12+2\sqrt{3}}}{4}\)

\(\Rightarrow2\cos\alpha=\dfrac{\sqrt{12+2\sqrt{3}}}{2}\). Chọn B.

1: \(\sqrt{3+\sqrt{5}}\cdot\sqrt{2}=\sqrt{6+2\sqrt{5}}=\sqrt{5}+1\)

3) \(\left(\sqrt{\dfrac{3}{4}}-\sqrt{3}+5\cdot\sqrt{\dfrac{4}{3}}\right)\cdot\sqrt{12}\)

\(=\left(\dfrac{\sqrt{3}}{2}-\dfrac{2\sqrt{3}}{2}+5\cdot\dfrac{2}{\sqrt{3}}\right)\cdot\sqrt{12}\)

\(=\dfrac{17\sqrt{3}}{6}\cdot2\sqrt{3}\)

\(=\dfrac{34\cdot3}{6}=\dfrac{102}{6}=17\)

Chia nhỏ ra bạn ơi!

\(a,=4\sqrt{6}-15\sqrt{6}+\sqrt{\left(2+\sqrt{6}\right)^2}=-11\sqrt{6}+2+\sqrt{6}=2-10\sqrt{6}\\ b,=\dfrac{\sqrt{3}\left(\sqrt{6}-2\right)}{\sqrt{6}-2}+\dfrac{4\left(\sqrt{3}-1\right)}{2}+\left|3\sqrt{3}-12\right|=\sqrt{3}+2\sqrt{3}-2+12-3\sqrt{3}=10\)