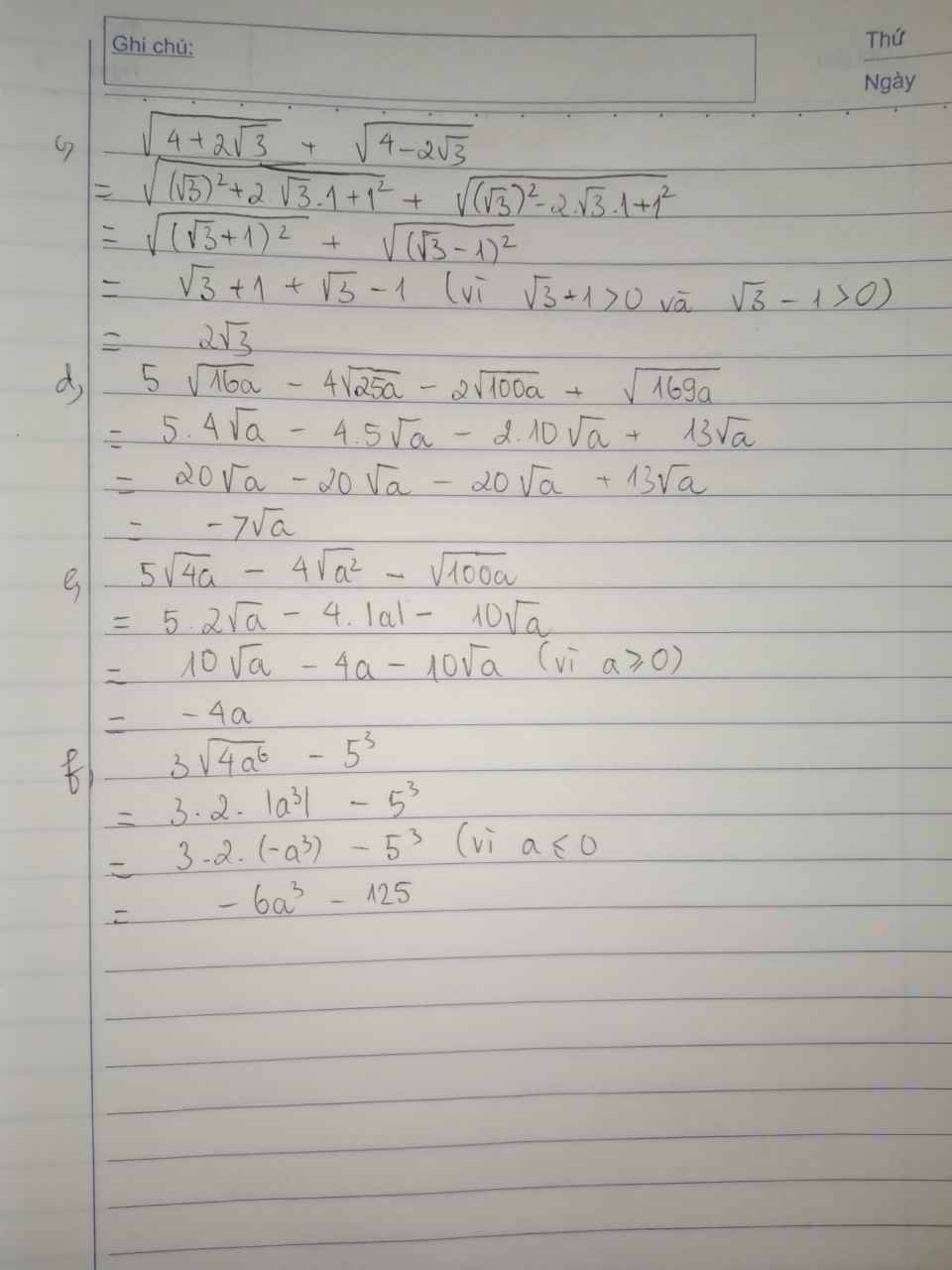Ta có:\(A=\left(\dfrac{a+4\sqrt{a}+4}{a+2\sqrt{a}}-\dfrac{\sqrt{a}}{\sqrt{a}-2}\right):\left(\dfrac{\sqrt{a}-4}{a-2\sqrt{a}}-\dfrac{3\sqrt{a}+6}{4-a}\right)\)

             \(=\left[\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}\left(\sqrt{a}+2\right)}-\dfrac{\sqrt{a}}{\sqrt{a}-2}\right]:\left[\dfrac{\sqrt{a}-4}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{3\left(\sqrt{a}+2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\right]\)

             \(=\dfrac{a-4-a-2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-2\right)}:\dfrac{\sqrt{a}-4+3\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-2\right)}\)

            \(=\dfrac{-4-2\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-2\right)}.\dfrac{\sqrt{a}\left(\sqrt{a}-2\right)}{4\sqrt{a}-4}=\dfrac{-2-\sqrt{a}}{2\sqrt{a}-2}\)

Ta có: \(A=\left(\dfrac{a+4\sqrt{a}+4}{a+2\sqrt{a}}-\dfrac{\sqrt{a}}{\sqrt{a}-2}\right):\left(\dfrac{\sqrt{a}-4}{a-2\sqrt{a}}-\dfrac{3\sqrt{a}+6}{4-a}\right)\)

\(=\left(\dfrac{\sqrt{a}+2}{\sqrt{a}}-\dfrac{\sqrt{a}}{\sqrt{a}-2}\right):\left(\dfrac{\sqrt{a}-4}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{3}{\sqrt{a}-2}\right)\)

\(=\dfrac{a-4-a}{\sqrt{a}\left(\sqrt{a}-2\right)}:\dfrac{\sqrt{a}-4+3\sqrt{a}}{\sqrt{a}\left(\sqrt{a}-2\right)}\)

\(=\dfrac{-4}{4\left(\sqrt{a}+1\right)}=\dfrac{-1}{\sqrt{a}+1}\)

ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne4\end{matrix}\right.\)

\(P=\left(\dfrac{\sqrt{a}-2}{\sqrt{a}+2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-2}\right)\cdot\left(\sqrt{a}-\dfrac{4}{\sqrt{ }a}\right)\)

\(=\dfrac{\left(\sqrt{a}-2\right)^2-\left(\sqrt{a}+2\right)^2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\cdot\dfrac{a-4}{\sqrt{a}}\)

\(=\dfrac{a-4\sqrt{a}+4-a-4\sqrt{a}-4}{\sqrt{a}}=\dfrac{-8\sqrt{a}}{\sqrt{a}}=-8\)

\(P=\left(\dfrac{\sqrt{a}-2}{\sqrt{a}+2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-2}\right)\left(\sqrt{a}-\dfrac{4}{\sqrt{a}}\right)\)     (ĐKXĐ: \(\left\{{}\begin{matrix}a>0\\a\ne4\end{matrix}\right.\))
\(=\left(\dfrac{\left(\sqrt{a}-2\right)^2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}-\dfrac{\left(\sqrt{a}+2\right)^2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\right)\left(\dfrac{a}{\sqrt{a}}-\dfrac{4}{\sqrt{a}}\right)\)
\(=\left(\dfrac{\left(\sqrt{a}-2\right)^2-\left(\sqrt{a}+2\right)^2}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\right)\left(\dfrac{a-4}{\sqrt{a}}\right)\)
\(=\left(\dfrac{\left(\sqrt{a}-2-\sqrt{a}-2\right)\left(\sqrt{a}-2+\sqrt{a}+2\right)}{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}\right)\left(\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}}\right)\)
\(=\dfrac{-4.2\sqrt{a}}{\sqrt{a}}\)
\(=-8\)
#YM

ĐKXĐ {a>0,a≠4}

\(P=\left(\dfrac{\sqrt{a}-2}{\sqrt{a}+2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-2}\right).\left(\sqrt{a}-\dfrac{4}{\sqrt{a}}\right)\)

\(P=\dfrac{\left(\sqrt{a}-2\right)^2-\left(\sqrt{a}+2\right)^2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}.\dfrac{a-4}{\sqrt{a}}\)

\(P=\dfrac{a-4\sqrt{a}+4-a-4\sqrt{a}-4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}.\dfrac{a-4}{\sqrt{a}}\)

\(P=\dfrac{-8\sqrt{a}}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}.\dfrac{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}{\sqrt{a}}\)

\(P=-8\)

\(A=2\cdot\sqrt{9+4\sqrt{5}}+\sqrt{5}-3\sqrt{5}\)

=2(căn 5+2)-2căn 5

=4

\(A=\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}\)

    \(=\sqrt{a-2+2\sqrt{a-2}.2+4}+\sqrt{a-2-2\sqrt{a-2}.2+4}\)

      \(=\sqrt{\left(\sqrt{a-2}\right)^2+2\sqrt{a-2}.2+2^2}+\sqrt{\left(\sqrt{a-2}\right)^2-2\sqrt{a-2}.2+2^2}\)

        \(=\sqrt{\left(\sqrt{a-2}+2\right)^2}+\sqrt{\left(\sqrt{a-2}-2\right)^2}\)

         \(=\left|\sqrt{a-2}+2\right|+\left|\sqrt{a-2}-2\right|\)

Ta có:

\(A=\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}\)

\(A=\sqrt{\left(\sqrt{a-2}\right)^2+2.2\sqrt{a-2}+2^2}+\sqrt{\left(\sqrt{a-2}\right)^2-2.2\sqrt{a-2}+2^2}\)

\(A=\sqrt{\left(\sqrt{a-2}+2\right)^2}+\sqrt{\left(\sqrt{a-2}-2\right)^2}\)

\(A=|\sqrt{a-2}+2|+|\sqrt{a-2}-2|\)   (1)

=> Điều kiên: a - 2 >= 0  <=> a >= 2

(1)  => \(A=\sqrt{a-2}+2+|\sqrt{a-2}-2|\)(Do số hạng đầu luôn lớn hơn 0 nên bỏ trị tuyệt đối)

TH1:  \(\sqrt{a-2}-2\ge0\Rightarrow A=\sqrt{a-2}+2+\sqrt{a-2}-2\)

           \(\sqrt{a-2}\ge2\Rightarrow A=2\sqrt{a-2}\)

          \(a\ge6\Rightarrow A=2\sqrt{a-2}\)

           (nhận)

TH2: \(\sqrt{a-2}-2\le0\Rightarrow A=\sqrt{a-2}+2-\sqrt{a-2}+2\)

            \(\sqrt{a-2}\le2\Rightarrow A=4\)

             \(2\le a\le6\Rightarrow A=4\) (Do đkxđ)

Vậy....

\(A=\sqrt{a+4\sqrt{a-2}+2}+\sqrt{a-4\sqrt{a-2}+2}\left(a\ge2\right)\)

\(A=\sqrt{\left(a-2\right)+4\sqrt{a-2}+4}+\sqrt{\left(a-2\right)-4\sqrt{a-2}+4}\)

\(A=\sqrt{\left(\sqrt{a-2}+2\right)^2}+\sqrt{\left(\sqrt{a-2}-2\right)^2}\)

\(A=\left|\sqrt{a-2}+2\right|+\left|\sqrt{a-2}-2\right|\)

\(A=\sqrt{a-2}+2+\left|\sqrt{a-2}-2\right|\)

\(A=\hept{\begin{cases}\sqrt{a-2}+2+\sqrt{a-2}-2\Leftrightarrow\sqrt{a-2}-2\ge0\\\sqrt{a+2}+2-\sqrt{a-2}+2\Leftrightarrow\sqrt{a-2}< 0\end{cases}}\)

\(A=\hept{\begin{cases}2\sqrt{a-2}\Leftrightarrow a-2\ge4\\4\Leftrightarrow a-2< 4\end{cases}}\)

\(A=\hept{\begin{cases}2\sqrt{a-2}\Leftrightarrow a\ge6\\4\Leftrightarrow a< 6\end{cases}}\)

Vậy \(A=\hept{\begin{cases}2\sqrt{a-2}\Leftrightarrow a\ge6\\4\Leftrightarrow2\le a\le6\end{cases}}\)

Đặt \(\sqrt[3]{a}=x;\sqrt[3]{b}=y\)

=>\(Q=\dfrac{x^4+x^2y^2+y^4}{x^2+xy+y^2}\)

\(=\dfrac{x^4+2x^2y^2+y^4-x^2y^2}{x^2+xy+y^2}\)

\(=\dfrac{\left(x^2+y^2\right)^2-\left(xy\right)^2}{x^2+xy+y^2}=\dfrac{\left(x^2-xy+y^2\right)\left(x^2+xy+y^2\right)}{x^2+xy+y^2}\)

\(=x^2-xy+y^2\)

\(=\sqrt[3]{a^2}-\sqrt[3]{ab}+\sqrt[3]{b^2}\)

Lời giải:

ĐKXĐ: $a\geq 0; a\neq 4$

\(A=\left[\frac{\sqrt{a}(\sqrt{a}-2)-\sqrt{a}(\sqrt{a}+2)}{(\sqrt{a}+2)(\sqrt{a}-2)}+\frac{4\sqrt{a}-1}{(\sqrt{a}-2)(\sqrt{a}+2)}\right].(\sqrt{a}+2)\)

\(=\frac{-4\sqrt{a}+4\sqrt{a}-1}{(\sqrt{a}-2)(\sqrt{a}+2)}.(\sqrt{a}+2)=\frac{-1}{(\sqrt{a}-2)(\sqrt{a}+2)}.(\sqrt{a}+2)=\frac{1}{2-\sqrt{a}}\)

\(P=\frac{\sqrt{a}+3}{\sqrt{a}-2}-\frac{\sqrt{a}-1}{\sqrt{a}+2}+\frac{4\sqrt{a}-4}{4-a}\)

\(=\frac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+2\right)}{a-4}-\frac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{a-4}-\frac{4\sqrt{a}-4}{a-4}\)

\(=\frac{a+5\sqrt{a}+6-\left(a-3\sqrt{a}+2\right)-\left(4\sqrt{a}-4\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)

\(=\frac{a+5\sqrt{a}+6-a+3\sqrt{a}-2-4\sqrt{a}+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\)

\(=\frac{4\sqrt{a}+8}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}=\frac{4\left(\sqrt{a}+2\right)}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}=\frac{4}{\sqrt{a}-2}\)

ĐKXĐ: \(x\ge2\)

\(A=\sqrt{x+2\sqrt{2x-4}}+\sqrt{x-2\sqrt{2x-4}}\)

\(=\sqrt{x-2+2.\sqrt{x-2}.\sqrt{2}+2}+\sqrt{x-2-2.\sqrt{x-2}.\sqrt{2}+2}\)

\(=\sqrt{\left(\sqrt{x-2}+\sqrt{2}\right)^2}+\sqrt{\left(\sqrt{x-2}-\sqrt{2}\right)^2}\)

\(=\left|\sqrt{x-2}+\sqrt{2}\right|+\left|\sqrt{x-2}-\sqrt{2}\right|=\sqrt{x-2}+\sqrt{2}+\left|\sqrt{x-2}-\sqrt{2}\right|\)

Xét \(x\ge4\Rightarrow\sqrt{x-2}\ge\sqrt{2}\)

\(\Rightarrow A=\sqrt{x-2}+\sqrt{2}+\sqrt{x-2}-\sqrt{2}=2\sqrt{x-2}\)

Xét \(0\le x< 4\Rightarrow\sqrt{x-2}< \sqrt{2}\)

\(\Rightarrow A=\sqrt{x-2}+\sqrt{2}-\sqrt{x-2}+\sqrt{2}=2\sqrt{2}\)