Cho các số dương a+b+c =1 Tìm giá trị lớn nhất của biểu thức P= \(\dfrac{ab}{c+1}\) + \(\dfrac{bc}{a+1}\) + \(\dfrac{ca}{b+1}\) . Làm ơn hãy giúp mình nhanh nha chiều mình thi rồi

Những câu hỏi liên quan
Cho a, b, c là các số thực dương khác 1. Hı̀nh vẽ bên là đồ thị của các hàm số
y
a
x
,
y
b
x
,
c
log
c
x
. Mệnh đề nào sau đây là đúng?
Đọc tiếp
Cho a, b, c là các số thực dương khác 1. Hı̀nh vẽ bên là đồ thị của các hàm số y = a x , y = b x , c = log c x . Mệnh đề nào sau đây là đúng?
![]()
![]()
![]()
![]()
Cho a, b, c là các số thực dương khác 1. Hı̀nh vẽ bên là đồ thị của các hàm số
y
a
x
,
y
b
x
,
y
log
c
x
. Mệnh đề nào sau đây là đúng? A.
a
b
c
B.
c
b
a...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1. Hı̀nh vẽ bên là đồ thị của các hàm số
y
=
a
x
,
y
=
b
x
,
y
=
log
c
x
. Mệnh đề nào sau đây là đúng?
A. a < b < c
B. c < b < a
C. a < c < b
D. c < a < b
1.Tìm tất cả các số nguyên dương n thoả mãn 4n4+1 là số nguyên tố
2.Cho 4 số nguyên dương a,b,c,d thoả mãn điều kiện ad= b2-bc+c2.Chứng minh rằng a2 +4b2+4c2+16d2 là hợp số
Ta có
n4 + 4 = n4 + 4n2 + 4 – 4n2
= (n2 + 2 )2 – (2n)2
= (n2 + 2 – 2n )(n2 + 2 + 2n)
Vì n4 + 4 là số nguyên tố nên n2 + 2 – 2n = 1 hoặc n2 + 2 + 2n = 1
Mà n2 + 2 + 2n > 1 vậy n2 + 2 – 2n = 1 suy ra n = 1
Thử lại : n = 1 thì 14 + 4 = 5 là số nguyên tố
Vậy với n = 1 thì n4 + 4 là số nguyên tố.
Đúng 0
Bình luận (0)
Ai giúp mình câu này với
Cho các số dương a,b,c có tích = 1. Chứng minh (a+1)(b+1)(c+1) lớn hơn hoặc bằng 8
chứng mimh các số nguyên dương a,b,c luôn > 1
a/a+b+b/b+c+c/c+a>1
các bạn giúp mk trả lời câu này vs
\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}\)
\(=\frac{a+b+c}{a+b+c}=1\Rightarrow\)đpcm
Đúng 0
Bình luận (0)
cho a,b,c,d là các số dương. chứng tỏ rằng:
1<a/a+b+c+b/b+c+d+c/c+d+a+d/d+a+b<2
cho a,b là các số dương. Chứng minh rằng \(\dfrac{1}{a}\)+\(\dfrac{1}{b}\)≥\(\dfrac{4}{a+b}\)
-Áp dụng BĐT Caushy Schwarz cho các cặp số dương (1,1) ở tử và (a,b) ở mẫu ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{\left(1+1\right)^2}{a+b}=\dfrac{4}{a+b}\)
-Dấu "=" xảy ra khi \(a=b\).
Đúng 0
Bình luận (0)
-Hoặc có thể c/m bằng phép biến đổi tương đương:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}\)
\(\Leftrightarrow\left(a+b\right)ab.\dfrac{a+b}{ab}\ge\dfrac{4}{a+b}.\left(a+b\right)ab\)
\(\Leftrightarrow\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2-4ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\) (luôn đúng)
-Dấu "=" xảy ra khi \(a=b\)
Đúng 0
Bình luận (0)
Cho a và b là các số nguyên dương
lim
x
→
0
a
a
x
-
1
sin
b
x
5
3
Tích có thể nhận giá trị bằng số nào trong các số dưới đây? A. 15. B. 60. C. 240. D. Cả ba đáp án trên.
Đọc tiếp
Cho a và b là các số nguyên dương lim x → 0 a a x - 1 sin b x = 5 3 Tích có thể nhận giá trị bằng số nào trong các số dưới đây?
A. 15.
B. 60.
C. 240.
D. Cả ba đáp án trên.
Chọn D.
Ta có 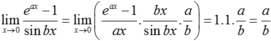
Vậy để 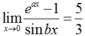 thì
thì 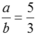 . Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
. Vì a và b là các số nguyên dương nên suy ra a = 5k, b = 3k với k nguyên dương. Do đó ab = 15k2.
+ 15k2 = 15 ⇔ k2 = 1 ⇒ k = 1 ⇒ ab = 15.
+ 15k2 = 60 ⇔ k2 = 4 ⇒ k = 2 ⇒ ab = 60.
+ 15k2 = 240 ⇔ k2 = 16 ⇒ k = 4 ⇒ ab = 240.
Vậy cả ba đáp án đều đúng.
Đúng 0
Bình luận (0)
Cho a,b,c là các số thực dương. CMR : \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{2}{a+b}+\dfrac{2}{b+c}+\dfrac{2}{a+c}\)
\(2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge\frac{4}{a+b}+\frac{4}{b+c}+\frac{4}{c+a}\) ( Svac-xơ, Cauchy các kiểu -,- )
\(\Leftrightarrow\)\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\ge\frac{\frac{4}{a+b}+\frac{4}{b+c}+\frac{4}{c+a}}{2}=\frac{2}{a+b}+\frac{2}{b+c}+\frac{2}{c+a}\) ( đpcm )
...
Đúng 0
Bình luận (0)
\(2VP=\frac{4}{a+b}+\frac{4}{b+c}+\frac{4}{c+a}\)
\(\le\frac{1}{a}+\frac{1}{b}+\frac{1}{b}+\frac{1}{c}+\frac{1}{c}+\frac{1}{a}=2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=2VT\)
Từ đây,ta có: \(2VT\ge2VP\Rightarrow VT\ge VP^{\left(đpcm\right)}\)
Đúng 0
Bình luận (0)
Cho các số dương a+b+c =1 Tìm giá trị lớn nhất của biểu thức \(P=\frac{ab}{c+1}+\frac{bc}{a+1}+\frac{ca}{b+1}\)
https://olm.vn/hoi-dap/detail/232384263245.html
Áp dụng BĐT \(\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
Ta có : \(\frac{ab}{c+1}=\frac{ab}{a+c+b+c}\le\frac{ab}{4}\left(\frac{1}{a+c}+\frac{1}{b+c}\right)=\frac{ab}{4\left(a+c\right)}\)
\(+\frac{ab}{4\left(b+c\right)}\)
Thiết lập tương tự và thu lại ta có :
\(P\)\(\le\left[\frac{ab}{4\left(a+c\right)}+\frac{ab}{4\left(b+c\right)}+\frac{bc}{4\left(a+b\right)}+\frac{bc}{4\left(a+c\right)}+\frac{ac}{4\left(a+b\right)}+\frac{ac}{4\left(b+c\right)}\right]\)
\(\Leftrightarrow P\le\frac{ab+bc}{4\left(a+c\right)}+\frac{bc+ac}{4\left(a+b\right)}+\frac{ab+ac}{4\left(b+c\right)}\)
\(\Leftrightarrow P\le\frac{b\left(a+c\right)}{4\left(a+c\right)}+\frac{c\left(a+b\right)}{4\left(a+b\right)}+\frac{a\left(b+c\right)}{4\left(b+c\right)}=\frac{a+b+c}{4}=\frac{1}{4}\)
Vậy \(P_{max}=\frac{1}{4}\)
Dấu " = " xảy ra khi \(a=b=c=\frac{1}{3}\)
Do a+b+c=1 nên \(P=\frac{ab}{a+b+2c}+\frac{bc}{2a+b+c}+\frac{ac}{a+2b+c}\)
Áp dụng bất đẳng thức: \(\frac{1}{a}+\frac{1}{b}\le\frac{4}{a+b}\)hay \(\frac{1}{a+b}\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\):
Ta có: \(\frac{ab}{a+b+2c_{ }}=\frac{ab}{\left(a+c\right)+\left(b+c\right)}\le\frac{ab}{4}\left(\frac{1}{a+c}+\frac{1}{b+c}\right)\)\(=\frac{1}{4}\left(\frac{ab}{a+c}+\frac{ab}{b+c}\right)\)
Tương tự: \(\frac{bc}{2a+b+c}\le\frac{1}{4}\left(\frac{bc}{a+b}+\frac{bc}{a+c}\right)\)
\(\frac{ac}{a+2b+c}\le\frac{1}{4}\left(\frac{ac}{a+b}+\frac{ac}{b+c}\right)\)
Do đó: P\(\le\frac{1}{4}\left(\frac{ab}{a+c}+\frac{ab}{b+c}+\frac{bc}{a+b}+\frac{bc}{a+c}+\frac{ac}{b+a}+\frac{ac}{b+c}\right)\)
=\(\frac{1}{4}\left[\left(\frac{ab}{a+c}+\frac{bc}{a+c}\right)+\left(\frac{ab}{b+c}+\frac{ac}{b+c}\right)+\left(\frac{bc}{a+b}+\frac{ac}{a+b}\right)\right]\)
=\(\frac{1}{4}\left(a+b+c\right)=\frac{1}{4}.1=\frac{1}{4}\)
Dấu "=" xảy ra khi và chỉ khi a=b=c=1/3




















