Giải phương trình sau:
sin2x + sinx - 2sin2x + cosx +1 =0
Giải phương trình:
1,\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
2,\(|cosx-sinx|+2sin2x=1\)
3,\(2sin2x-3\sqrt{6}|sinx+cosx|+8=0\)
4,\(cosx+\dfrac{1}{cosx}+sinx+\dfrac{1}{sinx}=\dfrac{10}{3}\)
1.
\(sin^3x+cos^3x=1-\dfrac{1}{2}sin2x\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(sinx+cosx\right)\left(1-sinx.cosx\right)=1-sinx.cosx\)
\(\Leftrightarrow\left(1-sinx.cosx\right)\left(sinx+cosx-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx.cosx=1\\sinx+cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}sin2x=2\left(vn\right)\\\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)=1\end{matrix}\right.\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\dfrac{1}{\sqrt{2}}\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+k2\pi\\x+\dfrac{\pi}{4}=\pi-\dfrac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\dfrac{\pi}{2}+k2\pi\end{matrix}\right.\)
2.
\(\left|cosx-sinx\right|+2sin2x=1\)
\(\Leftrightarrow\left|cosx-sinx\right|-1+2sin2x=0\)
\(\Leftrightarrow\left|cosx-sinx\right|-\left(cosx-sinx\right)^2=0\)
\(\Leftrightarrow\left|cosx-sinx\right|\left(1-\left|cosx-sinx\right|\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)=0\\\left|cosx-sinx\right|=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{4}=k\pi\\cos^2x+sin^2x-2sinx.cosx=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\1-sin2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{4}+k\pi\\x=\dfrac{k\pi}{2}\end{matrix}\right.\)
3.
\(2sin2x-3\sqrt{6}\left|sinx+cosx\right|+8=0\)
\(\Leftrightarrow2\left(sinx+cosx\right)^2-3\sqrt{6}\left|sinx+cosx\right|+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left|sinx+cosx\right|=\sqrt{6}\left(vn\right)\\\left|sinx+cosx\right|=\dfrac{\sqrt{6}}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left|sin\left(x+\dfrac{\pi}{4}\right)\right|=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{4}\right)=\pm\dfrac{\sqrt{3}}{2}\)
...
Phương trình 2 sin 2 x + sin x cos x - cos 2 x = 0 có nghiệm là:
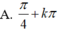


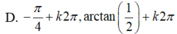
Phương trình 2sin2x + sinx. cosx – cos2x = 0 có nghiệm là:
![]()

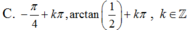
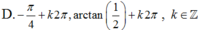
Hướng dẫn giải
Chọn C.
TH1: Nếu cosx =0 có sin2x = 1 không thỏa mãn phương trình.
TH2: ![]() chia cả hai vế của phương trình cho cos2x ta được:
chia cả hai vế của phương trình cho cos2x ta được:
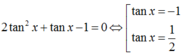
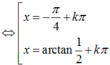
Phương trình 2sin2x - 3 6 |sinx + cosx| + 8 = 0 có nghiệm là
A. 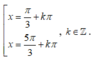
B. 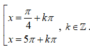
C. 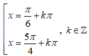
D. 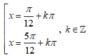
giải các pt
a) \(sinx+cosx-2sin2x-1=0\)
b) \(sinx+cosx+3sinx.cosx-1=0\)
c) \(sinx-2sin2x=\frac{1}{2}-cosx\)
d) \(6\left(sinx-cosx\right)-1=sinx.cosx\)
a/
\(\Leftrightarrow sinx+cosx-4sinx.cosx-1=0\)
Đặt \(sinx+cosx=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=t\Rightarrow\left|t\right|\le\sqrt{2}\)
\(\Rightarrow t^2=1+2sinx.cosx\Rightarrow sinx.cosx=\frac{t^2-1}{2}\)
Pt trở thành:
\(t-2\left(t^2-1\right)-1=0\)
\(\Leftrightarrow-2t^2+t+1=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1\\\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=-\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\\sin\left(x+\frac{\pi}{4}\right)=-\frac{1}{2\sqrt{2}}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\\x+\frac{\pi}{4}=arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\\x+\frac{\pi}{4}=\pi-arcsin\left(-\frac{1}{2\sqrt{2}}\right)+k2\pi\end{matrix}\right.\) \(\Rightarrow x=...\)
b/
Đặt \(sinx+cosx=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=t\Rightarrow sinx.cosx=\frac{t^2-1}{2}\)
Pt trở thành:
\(t+\frac{3}{2}\left(t^2-1\right)-1=0\)
\(\Leftrightarrow3t^2+2t-5=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1\\t=\frac{5}{3}>\sqrt{2}\left(l\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=-1\)
\(\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=-\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-\frac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
c/
\(\Leftrightarrow sinx+cosx-4sinx.cosx=\frac{1}{2}\)
Đặt \(sinx+cosx=\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=t\) với \(\left|t\right|\le\sqrt{2}\)
\(sinx.cosx=\frac{t^2-1}{2}\)
Pt trở thành:
\(t-2\left(t^2-1\right)=\frac{1}{2}\)
\(\Leftrightarrow-4t^2+2t+3=0\)
\(\Rightarrow\left[{}\begin{matrix}t=\frac{1+\sqrt{13}}{4}\\t=\frac{1-\sqrt{13}}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}sin\left(x+\frac{\pi}{4}\right)=\frac{1+\sqrt{13}}{4\sqrt{2}}\\sin\left(x+\frac{\pi}{4}\right)=\frac{1-\sqrt{13}}{4\sqrt{2}}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=arcsin\left(\frac{1+\sqrt{13}}{4\sqrt{2}}\right)+k2\pi\\x+\frac{\pi}{4}=\pi-arcsin\left(\frac{1+\sqrt{13}}{4\sqrt{2}}\right)+k2\pi\\x+\frac{\pi}{4}=arcsin\left(\frac{1-\sqrt{13}}{4\sqrt{2}}\right)+k2\pi\\x+\frac{\pi}{4}=\pi-arcsin\left(\frac{1-\sqrt{13}}{4\sqrt{2}}\right)+k2\pi\end{matrix}\right.\)
\(\Rightarrow x=...\)
giải phương trình: 3cosx(1 - cos2x) + 2sin2x + sinx + cos2x = 0
cos2x = 1- sin^x
sin2x= 2sinxcosx
Nhóm lại bình thường và giải thôi
Giải pt ( Phương trình đối xứng và nửa đối xứng)
a) \(1+tanx=2\sqrt{2}sinx\)
b) \(\left|cosx-sinx\right|+2sin2x=1\)
c) \(cos^3x+sin^3x=cos2x\)
d) \(cos^3x+sin^3x=2sin2x+sinx+cosx\)
e) \(cosx+\frac{1}{cosx}+sinx+\frac{1}{sinx}=\frac{10}{3}\)
chứng minh các bất pt sau:
sin2x+sinx/1+cos2x+cosx=tanx
giải phương trình lượng giác
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
ĐK: \(x\ne\dfrac{\pi}{6}+k2\pi;x\ne\dfrac{5\pi}{6}+k2\pi\)
\(\dfrac{cosx-\sqrt{3}sinx}{sinx-\dfrac{1}{2}}=0\)
\(\Leftrightarrow cosx-\sqrt{3}sinx=0\)
\(\Leftrightarrow\dfrac{1}{2}cosx-\dfrac{\sqrt{3}}{2}sinx=0\)
\(\Leftrightarrow cos\left(x+\dfrac{\pi}{3}\right)=0\)
\(\Leftrightarrow x+\dfrac{\pi}{3}=\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\)
Đối chiếu điều kiện ta được \(x=-\dfrac{5\pi}{6}+k2\pi\).