*Cho hàm số y=(m2 + 3m +4) x2
Chứng tỏ hàm số luôn nghịch biến trong khoảng (-∞; 0) (hay x<0) và đồng biến trong khoảng(0;+∞) (hay x>0)
Những câu hỏi liên quan
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Đúng 1
Bình luận (0)
Cho hàm số
y
m
2
-
3
m
+
2
x
4
-
x
3
+
m
-
2
x
2
-
x...
Đọc tiếp
Cho hàm số y = m 2 - 3 m + 2 x 4 - x 3 + m - 2 x 2 - x , có bao nhiêu giá trị nguyên của m để hàm số đã cho nghịch biến trên khoảng - ∞ ; + ∞ .
A. 2.
B. 0.
C. 1.
D. 3.
Khi đó y' là hàm số bậc ba. Phương trình y'=0 có ít nhất một nghiệm đơn hoặc bội lẻ và đổi dấu qua nghiệm đó. Do đó mệnh đề (*) sai. Suy ra loại m 2 - 3 m + 2 ≠ 0
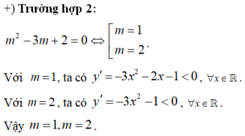
Chọn A
Đúng 0
Bình luận (0)
Hàm số
y
-
3
x
4
-
(
3
m
2
-
3
m
+
1
)
x
2
+
5...
Đọc tiếp
Hàm số y = - 3 x 4 - ( 3 m 2 - 3 m + 1 ) x 2 + 5 m 2 - 2 m + 2 nghịch biến trong khoảng nào?
A.
.
B.
.
C.
.
D.
.
Chọn B
Tập xác định của hàm số: 
Ta có: 
.
.
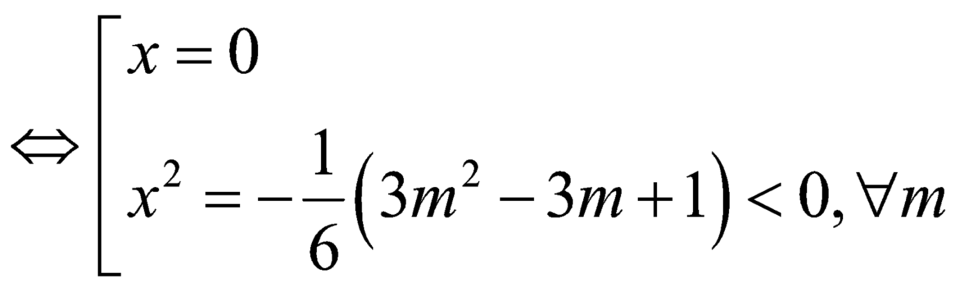
Vì 
nên hàm số nghịch biến trên khoảng 
.
Đúng 0
Bình luận (0)
bài 1 : Cho hàm số y=(m2-4m+3)x2
Tìm x để :
a, Hàm số đồng biến với x>0
b, hàm số nghịch biến với x>0
Bài 2 cho hàm số y=(m2-6m+12)x2
a, chứng tỏ rằng hàm số nghịch biến khi x<0 và đồng biến khi x>0
b,Khi m=2 tìm x để y=-2
c,khi m =5 tính giá trị của y biết x=1+căn 2
d, tìm m khi x=1 và y = 5
Cho hàm số \(y = \frac{1}{x}\). Chứng tỏ hàm số đã cho:
a) Nghịch biến trên khoảng \(\left( {0; + \infty } \right)\);
b) Nghịch biến trên khoảng \(\left( { - \infty ;0} \right)\).
a) Tập xác định \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
Lấy \({x_1},{x_2} \in \left( {0; + \infty } \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( {0; + \infty } \right) \Rightarrow {x_1}{x_2} > 0\)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\).
b) Lấy \({x_1},{x_2} \in \left( { - \infty ;0} \right)\) sao cho \({x_1} < {x_2}\).
Xét \(f\left( {{x_1}} \right) - f\left( {{x_2}} \right) = \frac{1}{{{x_1}}} - \frac{1}{{{x_2}}} = \frac{{{x_2} - {x_1}}}{{{x_1}{x_2}}}\)
Do \({x_1} < {x_2}\) nên \({x_2} - {x_1} > 0\)
\({x_1},{x_2} \in \left( { - \infty ;0} \right) \Rightarrow {x_1}{x_2} > 0\)(Cùng dấu âm nên tích cũng âm)
\( \Rightarrow f\left( {{x_1}} \right) - f\left( {{x_2}} \right) > 0 \Leftrightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Vậy hàm số nghịch biến trên \(\left( { - \infty ;0} \right)\).
Đúng 0
Bình luận (0)
Cho hàm số y=(m2+2m+3)x2 với giá trị nào của x thì:
a) Hàm số đồng biến
b) Hàm số nghịch biến
Do \(m^2+2m+3=\left(m+1\right)^2+2>0\) ; \(\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
Đúng 1
Bình luận (0)
Cho hàm số y f(x) . Đồ thị hàm số y f’(x) như hình bên. Hỏi hàm số y g(x) f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau? A. (1; 2) B. (0; + ∞) C. (-2; -1) D. (-1; 1)
Đọc tiếp
Cho hàm số y= f(x) . Đồ thị hàm số y= f’(x) như hình bên. Hỏi hàm số y= g(x) = f(1-x2) nghịch biến trên khoảng nào trong các khoảng sau?
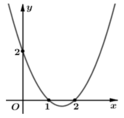
A. (1; 2)
B. (0; + ∞)
C. (-2; -1)
D. (-1; 1)
Cho hàm số yf(x) có đồ thị hàm số yf (x) như hình vẽ bên. Hàm số
y
f
(
x
2
-
2
)
-
1
3
x
3
-
x
2
+
3
x
-
4
nghịch biến trên khoảng nào dưới đây ? A.
-
∞...
Đọc tiếp
Cho hàm số y=f(x) có đồ thị hàm số y=f '(x) như hình vẽ bên. Hàm số y = f ( x 2 - 2 ) - 1 3 x 3 - x 2 + 3 x - 4 nghịch biến trên khoảng nào dưới đây ?
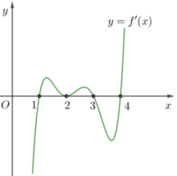
A. - ∞ ; - 3
B. - 3 ; 0
C. 1 ; 3
D. - 3 ; + ∞
Có 
Bất phương trình này khó giải trực tiếp, do vậy ta sẽ chọn x thoả mãn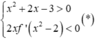 
TH1: Nếu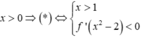 
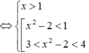
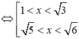
Chọn đáp án C.
TH2: Nếu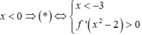 
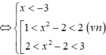
Đúng 0
Bình luận (0)
Hỏi có bao nhiêu số nguyên m để hàm số
(
m
2
-
1
)
x
3
+
(
m
-
1
)
x
2
-
x
+
4
nghịch biến trên khoảng (-¥,+¥)?
Đọc tiếp
Hỏi có bao nhiêu số nguyên m để hàm số ( m 2 - 1 ) x 3 + ( m - 1 ) x 2 - x + 4 nghịch biến trên khoảng (-¥,+¥)?
cho (d) y = ( m2 + 3m - 4 ) x -1 .
a) tìm m để (d) là hàm số bậc nhất b) ( d) đồng biến c) (d) nghịch biến
a: Để (d) là hàm số bậc nhất thì \(m^2+3m-4< >0\)
=>\(\left(m+4\right)\left(m-1\right)< >0\)
=>\(m\notin\left\{-4;1\right\}\)
b: Để (d) đồng biến thì \(m^2+3m-4>0\)
=>(m+4)(m-1)>0
=>m>1 hoặc m<-4
c: Để (d) nghịch biến thì m^2+3m-4<0
=>(m+4)(m-1)<0
=>-4<m<1
Đúng 0
Bình luận (0)