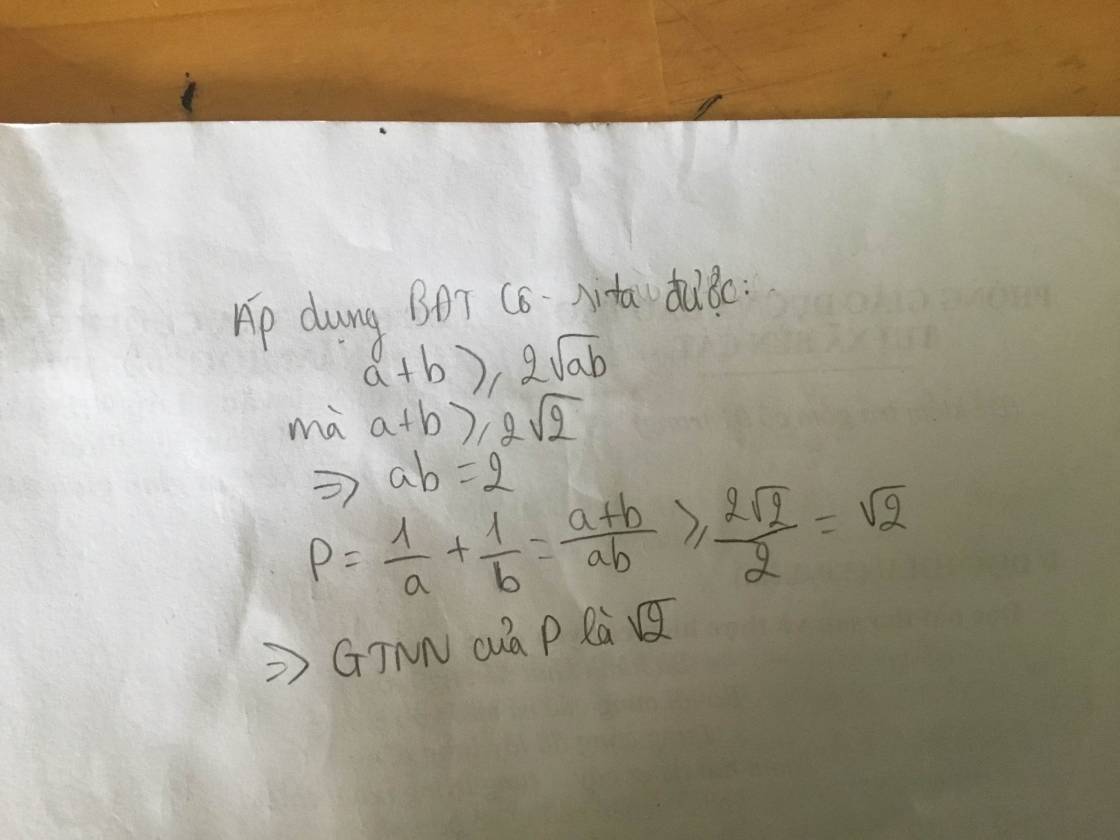a, \(y=\dfrac{\sqrt{x-2}}{x}=\sqrt{\dfrac{1}{x}-\dfrac{2}{x^2}}\ge0\)

\(min=0\Leftrightarrow\dfrac{1}{x}-\dfrac{2}{x^2}=0\Leftrightarrow x=2\)

b, Áp dụng BĐT Cosi:

\(f\left(x\right)=\dfrac{x}{\sqrt{x-1}}=\dfrac{x-1+1}{\sqrt{x-1}}=\sqrt{x-1}+\dfrac{1}{\sqrt{x-1}}\ge2\)

\(minf\left(x\right)=2\Leftrightarrow x=2\)

\(S=a^2+\dfrac{1}{a^2}\)

\(S=\dfrac{1}{16}a^2+\dfrac{1}{a^2}+\dfrac{15}{16}a^2\)

\(S\ge2\sqrt{\dfrac{1}{16}a^2\cdot\dfrac{1}{a^2}}+\dfrac{15}{16}\cdot2^2\)

\(S\ge2\cdot\dfrac{1}{4}+\dfrac{15}{4}\)

\(S\ge\dfrac{17}{4}\)

Vậy \(MINS=\dfrac{17}{4}\Leftrightarrow a=2\)

\(A=a+\dfrac{1}{a^2}=\dfrac{3}{4}a+\dfrac{a}{8}+\dfrac{a}{8}+\dfrac{1}{a^2}>=\dfrac{3}{4}\cdot2+\dfrac{3}{4}=\dfrac{27}{4}\)

Dấu = xảy ra khi a=2

1) Áp dụng bđt Cauchy cho 3 số dương ta có

 \(\dfrac{1}{x}+\dfrac{1}{x}+\dfrac{1}{x}+x^3\ge4\sqrt[4]{\dfrac{1}{x}.\dfrac{1}{x}.\dfrac{1}{x}.x^3}=4\) (1)

\(\dfrac{3}{y^2}+y^2\ge2\sqrt{\dfrac{3}{y^2}.y^2}=2\sqrt{3}\) (2)

\(\dfrac{3}{z^3}+z=\dfrac{3}{z^3}+\dfrac{z}{3}+\dfrac{z}{3}+\dfrac{z}{3}\ge4\sqrt[4]{\dfrac{3}{z^3}.\dfrac{z}{3}.\dfrac{z}{3}.\dfrac{z}{3}}=4\sqrt{3}\) (3)

Cộng (1);(2);(3) theo vế ta được

\(\left(\dfrac{3}{x}+\dfrac{3}{y^2}+\dfrac{3}{z^3}\right)+\left(x^3+y^2+z\right)\ge4+2\sqrt{3}+4\sqrt{3}\)

\(\Leftrightarrow3\left(\dfrac{1}{x}+\dfrac{1}{y^2}+\dfrac{1}{z^3}\right)\ge3+4\sqrt{3}\)

\(\Leftrightarrow P\ge\dfrac{3+4\sqrt{3}}{3}\)

Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{x}=x^3\\\dfrac{3}{y^2}=y^2\\\dfrac{3}{z^3}=\dfrac{z}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\sqrt[4]{3}\\z=\sqrt{3}\end{matrix}\right.\) (thỏa mãn giả thiết ban đầu)

2) Ta có \(4\sqrt{ab}=2.\sqrt{a}.2\sqrt{b}\le a+4b\)

Dấu"=" khi a = 4b

nên \(\dfrac{8}{7a+4b+4\sqrt{ab}}\ge\dfrac{8}{7a+4b+a+4b}=\dfrac{1}{a+b}\)

Khi đó \(P\ge\dfrac{1}{a+b}-\dfrac{1}{\sqrt{a+b}}+\sqrt{a+b}\)

Đặt \(\sqrt{a+b}=t>0\) ta được

\(P\ge\dfrac{1}{t^2}-\dfrac{1}{t}+t=\left(\dfrac{1}{t^2}-\dfrac{2}{t}+1\right)+\dfrac{1}{t}+t-1\)

\(=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\)

Có \(\dfrac{1}{t}+t\ge2\sqrt{\dfrac{1}{t}.t}=2\) (BĐT Cauchy cho 2 số dương)

nên \(P=\left(\dfrac{1}{t}-1\right)^2+\dfrac{1}{t}+t-1\ge\left(\dfrac{1}{t}-1\right)^2+1\ge1\)

Dấu "=" xảy ra <=> \(\left\{{}\begin{matrix}\dfrac{1}{t}-1=0\\t=\dfrac{1}{t}\end{matrix}\right.\Leftrightarrow t=1\)(tm)

khi đó a + b = 1

mà a = 4b nên \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)

Vậy MinP = 1 khi \(a=\dfrac{4}{5};b=\dfrac{1}{5}\)

Bạn tham khảo bài làm nhé

Ta sẽ áp dụng Côsi cho 3 số:xa+xa+1/a²

^Dự đoán "=" xảy ra <=> a=2 và xa=1/a²

=> x=1/8

khi đó ta có 

S= a+1/a² =(a/8+a/8+1/a²) +6a/8 >= 3 căn bậc 3 của( a/8. a/8. 1/a²) +(6×2)/8=9/4

VậyMinS=9/4 đặt đc khi a=2

\(P=\left(a^2+\dfrac{1}{16a^2}\right)+\left(b^2+\dfrac{1}{16b^2}\right)+\dfrac{15}{16}\left(\dfrac{1}{a^2}+\dfrac{1}{b^2}\right)\ge2\sqrt{\dfrac{a^2}{16a^2}}+2\sqrt{\dfrac{b^2}{16b^2}}+\dfrac{15}{32}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)^2\)

\(P\ge1+\dfrac{15}{32}.\left(\dfrac{4}{a+b}\right)^2\ge1+\dfrac{15}{32}.\left(\dfrac{4}{1}\right)^2=\dfrac{17}{2}\)

\(P_{min}=\dfrac{17}{2}\) khi \(a=b=\dfrac{1}{2}\)

Đề bài thiếu, để tìm min A; B cần thêm điều kiện a;b là số thực dương

ĐKXĐ: a<>1; a<>0; a<>-1

a: \(P=\dfrac{a\left(a+1\right)}{\left(a-1\right)^2}:\dfrac{a^2-1+a+2-a^2}{a\left(a-1\right)}\)

\(=\dfrac{a\left(a+1\right)}{\left(a-1\right)^2}\cdot\dfrac{a\left(a-1\right)}{a+1}=\dfrac{a^2}{a-1}\)

b: Khi P=-1/2 thì a^2/(a-1)=-1/2

=>2a^2=-a+1

=>2a^2+a-1=0

=>2a^2+2a-a-1=0

=>(a+1)(2a-1)=0

=>a=1/2(nhận) hoặc a=-1(loại)

c: \(P=\dfrac{a^2-1+1}{a-1}=a+1+\dfrac{1}{a-1}=a-1+\dfrac{1}{a-1}+2\)

=>\(P>=2\cdot\sqrt{\left(a-1\right)\cdot\dfrac{1}{a-1}}+2=4\)

Dấu = xảy ra khi a-1=1

=>a=2