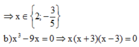Ta có: \(x^3+6x^2+9x=0\)

\(\Leftrightarrow x\left(x+3\right)^2=0\)

hay \(x\in\left\{0;-3\right\}\)

x³+6x²+9x=0

⇒x(x²+6x+9)=0

⇒x(x+3)²=0

⇒\(\left[{}\begin{matrix}x=0\\\left(x+3\right)^2=0\end{matrix}\right.\)

⇒\(\left[{}\begin{matrix}x=0\\x+3=0\end{matrix}\right.\)

⇒\(\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)

\(pt< =>x\left(x^2+6x+9\right)=0< =>x\left(x+3\right)^2=0\)

\(=>\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)

\(\left(5-x\right)\left(9x^2-4\right)=0\)

=>\(\left(x-5\right)\left(3x-2\right)\left(3x+2\right)=0\)

=>\(\left[{}\begin{matrix}x-5=0\\3x-2=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)

\(\left(5-x\right)\left(9x^2-4\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}5-x=0\\9x^2-4=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=5\\x^2=\dfrac{4}{9}\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=5\\x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)

a/ => x² + 3x - 10  = 0

=> x² - 2x + 5x - 10 = 0

=> x(x - 2) + 5(x - 2) = 0

=> (x - 2)(x + 5) = 0 

=> x - 2 = 0 => x = 2

hoặc x + 5 = 0 => x = -5

Vậy x = 2; x = -5

b/ => 3(x³ + 3x² + 3x + 1) = 0 

=> x³ + 3x² + 3x + 1 = 0 

=> (x + 1)³ = 0 

=> x + 1 = 0 => x = -1

Vậy x = -1

\(\left|x^3+x\right|-\left|9x^2+9\right|=0\)

\(\Leftrightarrow\left|x\left(x^2+1\right)\right|-9\left|x^2+1\right|=0\)

\(\Leftrightarrow\left(\left|x\right|-9\right)\left(x^2+1\right)=0\)

\(\Leftrightarrow\left|x\right|=9\left(x^2+1\ge1>0\right)\Leftrightarrow x=\pm9\)

Vậy ... 

\(\left|x^3+x\right|-\left|9x^2+9\right|=0\)

\(TH1:\left\{{}\begin{matrix}\left|x^3+x\right|=0\\\left|9x^2+9\right|=0\end{matrix}\right.\)

\(\text{Vì }9x^2\ge0\)

\(\Rightarrow9x^2+9\ge9\)

\(TH2:\left|x^3+x\right|=\left|9x^2+9\right|\)

\(\Rightarrow\left[{}\begin{matrix}x^3+x=9x^2-9\\x^3+x=9x^2+9\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x^3+x+9x^2+9=0\\x^3+x-9x^2-9=0\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x.\left(x^2+1\right)+9.\left(x^2+1\right)=0\\x.\left(x^2+1\right)-9.\left(x^2+1\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=9\end{matrix}\right.\)

=>|x^3+x|=|9x^2+9|

=>x^3+x=9x^2+9 hoặc x^3+x=-9x^2-9

=>x^3-9x^2+x-9=0 hoặc x^3+9x^2+x+9=0

=>x+9=0 hoặc (x-9)(x^2+1)=0

=>x=9 hoặc x=-9

9x²-6x-3=0

=>9x²-9x+3x-3=0

=>(x-1)(9x-3)=0

=>x-1=0 hoặc 9x+3 = 0

=> x=1 hoặc x=-1/3

b. x³+9x²+27x+19=0

   x³+x²+8x²+8x+19x+19=0

(x+1)(x²+8x+19)=0

x+1=0 => x=-1 

x²+8x+19= x²+8x+16+3=(x+4)²+3 lớn hơn hoặc bằng 3., lớn hơn 0 với moị x

a, \(\Rightarrow3\left(3x^2-2x-1\right)=0\)

\(\Rightarrow3x^2-2x-1=0\)

\(\Rightarrow x\left(3x-2\right)=1\)

\(\Rightarrow\orbr{\begin{cases}x=1\\3x-2=1\end{cases}\Rightarrow\orbr{\begin{cases}x=1\\x=1\end{cases}}}\)

\(\Rightarrow\orbr{\begin{cases}x=-1\\3x-2=-1\end{cases}\Rightarrow}\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}\)

b,\(\Rightarrow x^3+3x^2+6x^2+9x+18x+19=0\)

\(\Rightarrow x^2\left(x+3\right)+3x\left(x+3\right)+18\left(x+3\right)-2=0\)

\(\Rightarrow\left(x+3\right)\left(x^2+3x+18\right)=2\)

Mk k co thoi gian. buoc tiep theo tu lam not nhe

<=>\(9x^2-6x+1-4=0\)

<=>\(\left(3x-1\right)^2-4=0\)

<=>\(\left(3x-1\right)^2=4\)

<=>\(\left(3x-1\right)^2=2^2\)

<=>3x-1=2

<=>3x=3

<=>x=1

Vậy x=1

\(x^3-4x^2-9x+36=0\)

\(x^2\left(x-4\right)-9\left(x-4\right)=0\)

\(\left(x-4\right)\left(x^2-9\right)=0\)\(\)

\(\Rightarrow x-4=0\) hay \(x^2-9=0\)

\(\Rightarrow x=4\) hay \(x^2=9=3^2\)

\(\Rightarrow x=4\) hay \(x=\pm3\)

⇔x²(x-4) -9(x-4) = 0

⇔(x-4).(x-3).(x+3) = 0

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x-3=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=3\\x=-3\end{matrix}\right.\)

a)\(4x^3-9x=0\Leftrightarrow x\left(4x^2-9\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\4x^2-9=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=\frac{9}{4}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)

Vậy x = 0 hoặc \(x=\frac{3}{2}\)

b) \(x^3+8x=0\Leftrightarrow x\left(x^2+8\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=0\\x^2+8=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x^2=-8\left(L\right)\end{cases}}\)

Vậy x = 0

c) \(-x^3+9x=0\Leftrightarrow x\left(-x^2+9\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}-x^2+9=0\\x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x^2=9\\x=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=0\end{cases}}\)

Vậy ...