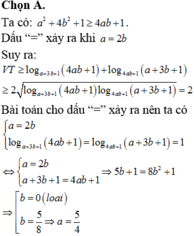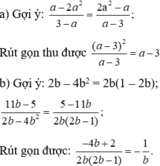c) 3a.4b2-0,8b.4b2-2ab.3b+b.3b2-1

Những câu hỏi liên quan
Cho hai số thực a và b thỏa mãn
log
a
+
3
b
+
1
a
2
+
4
b
2
+
1
+
log
4
a
b...
Đọc tiếp
Cho hai số thực a và b thỏa mãn log a + 3 b + 1 a 2 + 4 b 2 + 1 + log 4 a b + 1 a + 3 b + 1 = 2 . Khi đó giá trị của biểu thức P=6a+b là
A. 15/8
B. 25/8
C.15/4
D. 25/4
a) Tìm x,y thỏa mãn x3+y3 +1=3xy tính P= (1+1/x)(1+1/y)(x+y)
b) Cho a+2b+c=0 Tính P= a2/2ab + 4b2/ac + c2/2ab
c) Cho x,y Thỏa mãn x3+y3+8=6xy Tính P=(1 + z/y)(1 + z/x)(x+y)
giúp mik với ạ cảm ơn nhiều nhiều!!!
Thực hiện phép cộng các phân thức sau:a)
2
−
a
2
a
−
3
+
a
−
2
a
2
3
−
a
+
7
−...
Đọc tiếp
Thực hiện phép cộng các phân thức sau:
a) 2 − a 2 a − 3 + a − 2 a 2 3 − a + 7 − 5 a a − 3 với a ≠ 3 ;
b) 3 − 3 b 2 b + 3 b − 1 2 b − 1 + 11 b − 5 2 b − 4 b 2 với b ≠ 0 và b ≠ 1 2
Phân tích đa thức thành nhân tử:
1) a2 - 2b - 4b2 - 4b
2) x3 + 2x2 - 2x - 1
Mong mn giúp đỡ ạ:<<<<
1: \(a^2-4b^2-2a-4b\)
\(=\left(a-2b\right)\left(a+2b\right)-2\left(a+2b\right)\)
\(=\left(a+2b\right)\left(a-2b-2\right)\)
2: \(x^3+2x^2-2x-1\)
\(=\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+3x+1\right)\)
Đúng 0
Bình luận (0)
Cho a2+4b2+9c2=1. Tìm min và max của a+b+c
Đặt \(P=a+b+c\)
\(P^2=\left(a+b+c\right)^2=\left(1.a+\dfrac{1}{2}.2b+\dfrac{1}{3}.3c\right)^2\le\left(1^2+\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{3}\right)^2\right)\left(a^2+4b^2+9c^2\right)\)
\(\Rightarrow P^2\le\dfrac{49}{36}\left(a^2+4b^2+9c^2\right)=\dfrac{49}{36}\)
\(\Rightarrow-\dfrac{7}{6}\le P\le\dfrac{7}{6}\)
\(P_{min}=-\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(-\dfrac{6}{7};-\dfrac{3}{14};-\dfrac{2}{21}\right)\)
\(P_{max}=\dfrac{7}{6}\) khi \(\left(a;b;c\right)=\left(\dfrac{6}{7};\dfrac{3}{14};\dfrac{2}{21}\right)\)
Đúng 4
Bình luận (0)
Cho a; b; c là ba cạnh của 1 tam giác .CMR: (a+b+c)2+(a-b+c)2>4b2
\(\Leftrightarrow\left(a+c\right)^2+b^2+2b\left(a+c\right)+\left(a+c\right)^2+b^2-2b\left(a+c\right)>4b^2\)
\(\Leftrightarrow\left(a+c\right)^2>b^2\)
\(\Leftrightarrow a+c>b\) (luôn đúng theo BĐT tam giác)
Vậy BĐT đã cho được chứng minh
Đúng 0
Bình luận (0)
Cho \(\dfrac{a+b}{3}\)=\(\dfrac{b+c}{5}\)=\(\dfrac{c+a}{6}\) cmr ac-4b2 là số chính phương
\(\dfrac{a+b}{3}=\dfrac{b+c}{5}=\dfrac{c+a}{6}\\ \Leftrightarrow\left\{{}\begin{matrix}5a+5b=3b+3c\\5c+5a=6b+6c\\6a+6b=3c+3a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5a+2b-3c=0\left(1\right)\\5a-6b-c=0\left(2\right)\\a+2b-c=0\left(3\right)\end{matrix}\right.\)
Từ \(\left(1\right)\left(2\right)\Leftrightarrow8b-4c=0\Leftrightarrow2b=c\)
Từ \(\left(1\right)\left(3\right)\Leftrightarrow4a-4c=0\Leftrightarrow a-c=0\Leftrightarrow a=c=2b\)
\(\Leftrightarrow ac-4b^2=2b.2b-4b^2=4b^2-4b^2=0\left(đpcm\right)\)
Đúng 0
Bình luận (0)
Thu gọn các đa thức
a)\(2a^2x^3-ax^3-a^4-a^2x^3-ax^3+2a^4\) b)\(3xx^4+4xx^3-5x^2x^3-5x^2x^2\)
c)\(3a.4b^2-0,8b.4b^2-2ab.3b+b.3b^2-1\) d)\(5x.2y^2-5x.3xy-x^2y+6xy^2\)
Thu gọn đa thức
a, 2a2x3-ax3-a4-x3a2-ax3-2x4
b,3xx4+4xx3-5x2x3-5x2x2
c, 3a-4b2-0,8b . 4b2-2ab . 3b + b . 3b2-1
d, 5x.2y2-5x.3xy-x2y + 6xy2
Bài làm
a) 2a²x³ - ax³ - a⁴ - x³a² - ax³ - 2x⁴
= 2a²x³ - ax³ - a⁴ - a²x³ - ax³ - 2x⁴
= ( 2a²x³ - a²x³ ) - ( ax³ + ax³ ) - a⁴ - 2ax⁴
= a²x³ - 2ax³ - a⁴ - 2ax⁴
b) 3xx⁴ + 4xx³ - 5x²x³ - 5x²x²
= 3x⁵ + 4x⁴ - 5x⁵ - 5x⁴
= ( 3x⁵ - 5x⁵ ) + ( 4x⁴ - 5x⁴ )
= -2x⁵ - x⁴
c) 3a - 4b² - 0,8b . 4b² - 2ab . 3b + b . 3b² - 1
= 3a - 4b² - 3,2b³ - 6ab² + 3b³ - 1
= 3a - 4b² - 0,2b³ - 6ab² - 1
d) 5x.2y² - 5x.3xy - x²y + 6xy²
= 10xy² - 15x²y - x²y + 6xy²
= ( 10xy² + 6xy² ) - ( 15x²y + x²y )
= 16xy² - 16x²y
a)\(2a^2\)\(x^3\)-\(ax^3\)-\(a^4\)-\(x^3a^2\)-\(ax^3\)-\(2x^4\)
=(\(2a^2x^3-x^3a^2)\)+\((-ax^3-ax^3)\)-\(ax^4-2x^4\)
=\(a^2x^3-2ax^3-ax^4-2x^4\)
b)\(3xx^4+4xx^3-5x^2x^3-5x^2x^2
\)
=\(3x^5+4x^4-5x^5-5x^4\)
=\((3x^5-5x^5)+(4x^4-5x^4)\)
=\(-2x^5-x^4\)
d)\(5x.2y^2-5x.3xy-x^2y+6xy^2\)
=\((5.2)xy^2+(-5.3)xxy-x^2y+6xy^2\)
=\(10xy^2-15x^2y-x^2y+6xy^2\)
=\((10xy^2+6xy^2)+(-15x^2y-x^2y)\)
=\(16xy^2-16x^2y\)
câu c) mik ko biết làm