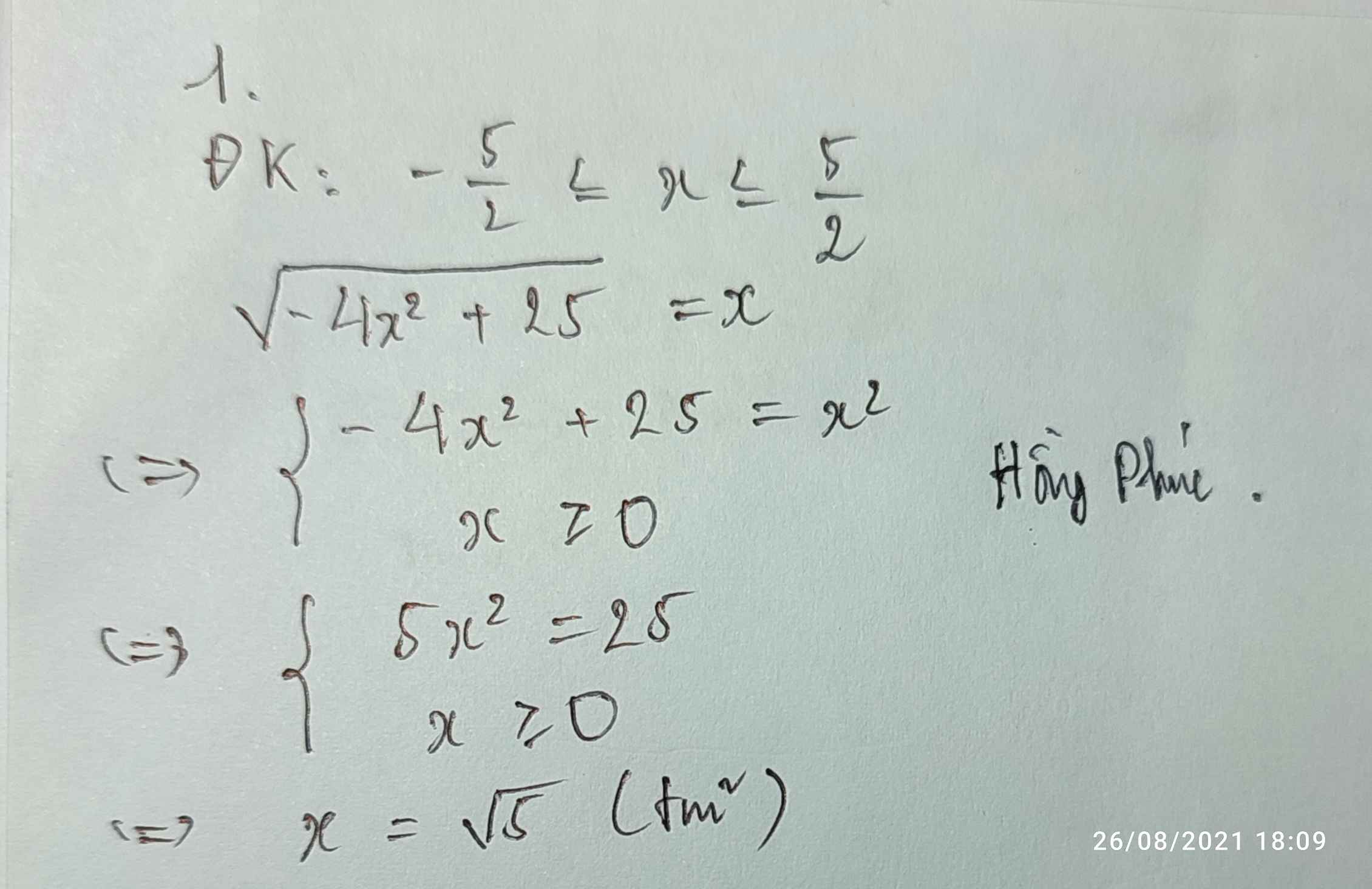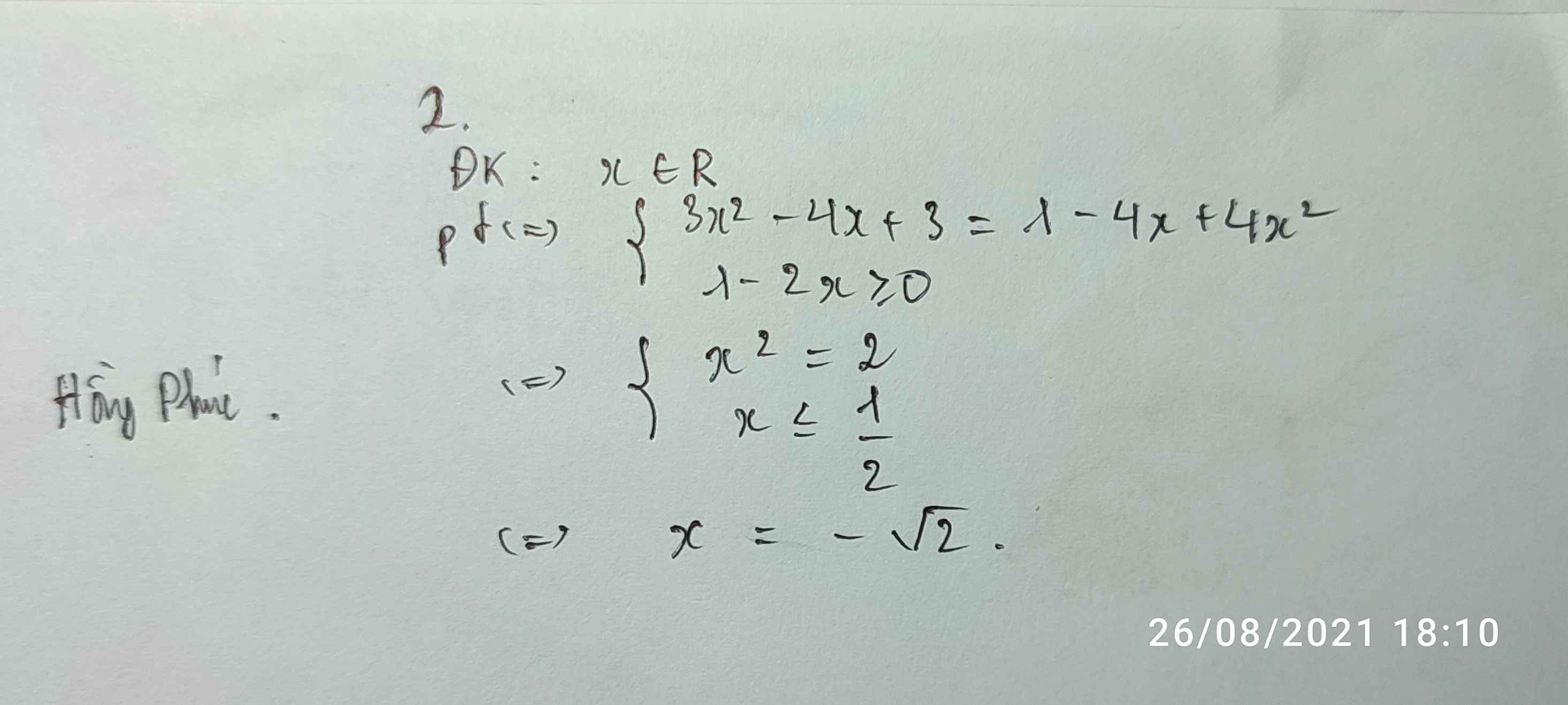\(x-3\sqrt{x}=0\)

Những câu hỏi liên quan
Tìm x ≥ 0, biết:
a) 2x-7\(\sqrt{x}\)+3=0
b) 3\(\sqrt{x}\)+5 < 6
c) x-3\(\sqrt{x}\) -10 < 0
d) x- 5\(\sqrt{x}\) +6 = 0
e) x+ 5\(\sqrt{x}\) -14 < 0
\(\left(a\right):2x-7\sqrt{x}+3=0\left(x\ge0\right)\\ < =>\left(2x-6\sqrt{x}\right)-\left(\sqrt{x}-3\right)=0\\ < =>2\sqrt{x}\left(\sqrt{x}-3\right)-\left(\sqrt{x}-3\right)=0\\ < =>\left(2\sqrt{x}-1\right)\left(\sqrt{x}-3\right)=0\\ =>\left[{}\begin{matrix}2\sqrt{x}-1=0\\\sqrt{x}-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=\dfrac{1}{4}\left(TM\right)\\x=9\left(TM\right)\end{matrix}\right.\)
\(\left(b\right):3\sqrt{x}+5< 6\\ < =>3\sqrt{x}< 1\\ < =>\sqrt{x}< \dfrac{1}{3}\\ < =>0\le x< \dfrac{1}{9}\)
\(\left(c\right):x-3\sqrt{x}-10< 0\\ < =>\left(x-5\sqrt{x}\right)+\left(2\sqrt{x}-10\right)< 0\\ < =>\sqrt{x}\left(\sqrt{x}-5\right)+2\left(\sqrt{x}-5\right)< 0\\ < =>\left(\sqrt{x}-5\right)\left(\sqrt{x}+2\right)< 0\\ =>\left\{{}\begin{matrix}\sqrt{x}-5< 0\\\sqrt{x}+2>0\end{matrix}\right.\\ < =>\left\{{}\begin{matrix}0\le x< 25\\x\ge0\end{matrix}\right.< =>0\le x< 25\)
\(\left(d\right):x-5\sqrt{x}+6=0\left(x\ge0\right)\\ < =>\left(x-2\sqrt{x}\right)-\left(3\sqrt{x}-6\right)=0\\ < =>\sqrt{x}\left(\sqrt{x}-2\right)-3\left(\sqrt{x}-2\right)=0\\ < =>\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)=0\\ =>\left[{}\begin{matrix}\sqrt{x}-3=0\\\sqrt{x}-2=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=9\\x=4\end{matrix}\right.\left(TM\right)\)
\(\left(e\right):x+5\sqrt{x}-14< 0\\ < =>\left(x+7\sqrt{x}\right)-\left(2\sqrt{x}+14\right)< 0\\ < =>\sqrt{x}\left(\sqrt{x}+7\right)-2\left(\sqrt{x}+7\right)< 0\\ < =>\left(\sqrt{x}-2\right)\left(\sqrt{x}+7\right)< 0\\ =>\left\{{}\begin{matrix}\sqrt{x}+7>0\\\sqrt{x}-2< 0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x\ge0\\0\le x< 4\end{matrix}\right.< =>0\le x< 4\)
Đúng 3
Bình luận (0)
1) x-\(7\sqrt{x-3}\) -9=0 2) \(\sqrt{x+3}\) =5-\(\sqrt{x-2}\) 3) \(\sqrt{x-4\sqrt{x+4}}\) =3 4) \(\sqrt{8-\dfrac{2}{3}x}-5\sqrt{2}\) =0 5) \(\sqrt{x^2-4x+4}\) =2-x
\(Q=\left(\dfrac{1}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\right)+\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right)\)
Rút gọn Q với x>0, x≠0, x≠9
\(Q=\dfrac{\sqrt{x}-3-\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{x-1-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{8}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{-6\sqrt{x}+1+8\sqrt{x}+24}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\\ Q=\dfrac{2\sqrt{x}+25}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)}\)
Đúng 1
Bình luận (0)
a : dfrac{3}{sqrt{x}-5}+dfrac{20-2sqrt{x}}{x-25}với x ≥ 0 x ≠ 25b : dfrac{sqrt{x}}{sqrt{x}-3}+dfrac{2sqrt{x}-2}{x-9}với x ≥ 0 x ≠ 9c : dfrac{sqrt{x}-1}{sqrt{x}+2}+dfrac{5sqrt{x}-2}{x-4}với x ≥ 0 x ≠ 4d : left(dfrac{x-2}{x+2sqrt{x}}+dfrac{1}{sqrt{x}+2}right).dfrac{sqrt{x}+1}{sqrt{x}-1}với ≥ 0 x ≠ 1
Đọc tiếp
a : \(\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\)với x ≥ 0 x ≠ 25
b : \(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\)với x ≥ 0 x ≠ 9
c : \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\)với x ≥ 0 x ≠ 4
d : \(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)với ≥ 0 x ≠ 1
\(a,\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\\ =\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{3\left(\sqrt{x}+5\right)}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}+\dfrac{20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{3\sqrt{x}+15+20-2\sqrt{x}}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\\ =\dfrac{\sqrt{x}+35}{\left(\sqrt{x}-5\right)\left(\sqrt{x}+5\right)}\)
Đúng 0
Bình luận (0)
\(b,\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x-9}+\dfrac{2\sqrt{x}-2}{x-9}\\ =\dfrac{x+3\sqrt{x}+2\sqrt{x}-2}{x-9}\\ =\dfrac{x-5\sqrt{x}-2}{x-9}\)
Đúng 0
Bình luận (0)
a: \(\dfrac{3}{\sqrt{x}-5}+\dfrac{20-2\sqrt{x}}{x-25}\)
\(=\dfrac{3\sqrt{x}+15+20-2\sqrt{x}}{x-25}=\dfrac{\sqrt{x}+35}{x-25}\)
b: \(\dfrac{\sqrt{x}}{\sqrt{x}-3}+\dfrac{2\sqrt{x}-2}{x-9}\)
\(=\dfrac{x+3\sqrt{x}+2\sqrt{x}-2}{x-9}=\dfrac{x+5\sqrt{x}-2}{x-9}\)
c: \(\dfrac{\sqrt{x}-1}{\sqrt{x}+2}+\dfrac{5\sqrt{x}-2}{x-4}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)+5\sqrt{x}-2}{x-4}\)
\(=\dfrac{x-3\sqrt{x}+2+5\sqrt{x}-2}{x-4}=\dfrac{x+2\sqrt{x}}{x-4}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
d: \(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{x-2+\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giải các phương trình sau:
a \(x^2-11=0\)
b \(x^2-12x+52=0\)
c \(x^2-3x-28=0\)
d \(x^2-11x+38=0\)
e \(6x^2+71x+175=0\)
f \(x^2-\left(\sqrt{2}+\sqrt{8}\right)x+4=0\)
g\(\left(1+\sqrt{3}\right)x^2-\left(2\sqrt{3}+1\right)x+\sqrt{3}=0\)
a.
$x^2-11=0$
$\Leftrightarrow x^2=11$
$\Leftrightarrow x=\pm \sqrt{11}$
b. $x^2-12x+52=0$
$\Leftrightarrow (x^2-12x+36)+16=0$
$\Leftrightarrow (x-6)^2=-16< 0$ (vô lý)
Vậy pt vô nghiệm.
c.
$x^2-3x-28=0$
$\Leftrightarrow x^2+4x-7x-28=0$
$\Leftrightarrow x(x+4)-7(x+4)=0$
$\Leftrightarrow (x+4)(x-7)=0$
$\Leftrightarrow x+4=0$ hoặc $x-7=0$
$\Leftrightarrow x=-4$ hoặc $x=7$
Đúng 2
Bình luận (0)
d.
$x^2-11x+38=0$
$\Leftrightarrow (x^2-11x+5,5^2)+7,75=0$
$\Leftrightarrow (x-5,5)^2=-7,75< 0$ (vô lý)
Vậy pt vô nghiệm
e.
$6x^2+71x+175=0$
$\Leftrightarrow 6x^2+21x+50x+175=0$
$\Leftrightarrow 3x(2x+7)+25(2x+7)=0$
$\Leftrightarrow (3x+25)(2x+7)=0$
$\Leftrightarrow 3x+25=0$ hoặc $2x+7=0$
$\Leftrightarrow x=-\frac{25}{3}$ hoặc $x=-\frac{7}{2}$
Đúng 3
Bình luận (0)
f.
$x^2-(\sqrt{2}+\sqrt{8})x+4=0$
$\Leftrightarrow x^2-\sqrt{2}x-2\sqrt{2}x+4=0$
$\Leftrightarrow x(x-\sqrt{2})-2\sqrt{2}(x-\sqrt{2})=0$
$\Leftrightarrow (x-\sqrt{2})(x-2\sqrt{2})=0$
$\Leftrightarrow x-\sqrt{2}=0$ hoặc $x-2\sqrt{2}=0$
$\Leftrightarrow x=\sqrt{2}$ hoặc $x=2\sqrt{2}$
g.
$(1+\sqrt{3})x^2-(2\sqrt{3}+1)x+\sqrt{3}=0$
$\Leftrightarrow (1+\sqrt{3})x^2-(1+\sqrt{3})x-(\sqrt{3}x-\sqrt{3})=0$
$\Leftrightarrow (1+\sqrt{3})x(x-1)-\sqrt{3}(x-1)=0$
$\Leftrightarrow (x-1)[(1+\sqrt{3})x-\sqrt{3}]=0$
$\Leftrightarrow x-1=0$ hoặc $(1+\sqrt{3})x-\sqrt{3}=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{3-\sqrt{3}}{2}$
Đúng 3
Bình luận (0)
Xem thêm câu trả lời
1, \(\sqrt{x-1}+\sqrt{x-4}=5\)
2, \(2x-7\sqrt{x}+5=0\)
3, \(\sqrt{2x+1}+\sqrt{x-3}=2\sqrt{x}\)
4, \(x-4\sqrt{x}+2021\sqrt{x-4}+4=0\)
5, \(\sqrt{2x-3}-\sqrt{x+1}=7\left(4-x\right)\)
1. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow \sqrt{x-1}=5-\sqrt{x-4}$
$\Rightarrow x-1=25+x-4-10\sqrt{x-4}$
$\Leftrightarrow 22=10\sqrt{x-4}$
$\Leftrightarrow 2,2=\sqrt{x-4}$
$\Leftrightarrow 4,84=x-4\Leftrightarrow x=8,84$
(thỏa mãn)
2. ĐKXĐ: $x\geq 0$
PT $\Leftrightarrow (2x-2\sqrt{x})-(5\sqrt{x}-5)=0$
$\Leftrightarrow 2\sqrt{x}(\sqrt{x}-1)-5(\sqrt{x}-1)=0$
$\Leftrightarrow (\sqrt{x}-1)(2\sqrt{x}-5)=0$
$\Leftrightarrow \sqrt{x}-1=0$ hoặc $2\sqrt{x}-5=0$
$\Leftrightarrow x=1$ hoặc $x=\frac{25}{4}$ (tm)
Đúng 1
Bình luận (0)
3. ĐKXĐ: $x\geq 3$
Bình phương 2 vế thu được:
$3x-2+2\sqrt{(2x+1)(x-3)}=4x$
$\Leftrightarrow 2\sqrt{(2x+1)(x-3)}=x+2$
$\Leftrightarrow 4(2x+1)(x-3)=(x+2)^2$
$\Leftrightarrow 4(2x^2-5x-3)=x^2+4x+4$
$\Leftrightarrow 7x^2-24x-16=0$
$\Leftrightarrow (x-4)(7x+4)=0$
Do $x\geq 3$ nên $x=4$
Thử lại thấy thỏa mãn
Vậy $x=4$
Đúng 2
Bình luận (0)
4. ĐKXĐ: $x\geq 4$
PT $\Leftrightarrow (x-4\sqrt{x}+4)+2021\sqrt{x-4}=0$
$\Leftrightarrow (\sqrt{x}-2)^2+2021\sqrt{x-4}=0$
Ta thấy, với mọi $x\geq 4$ thì:
$(\sqrt{x}-2)^2\ge 0$
$2021\sqrt{x-4}\geq 0$
Do đó để tổng của chúng bằng $0$ thì:
$\sqrt{x}-2=\sqrt{x-4}=0$
$\Leftrightarrow x=4$ (tm)
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
1.\(\sqrt{-4x^2+25}=x\)
2.\(\sqrt{3x^2-4x+3}=1-2x\)
3. \(\sqrt{4\left(1-x\right)^2}-\sqrt{3}=0\)
4.\(\dfrac{3\sqrt{x+5}}{\sqrt{ }x-1}< 0\)
5. \(\dfrac{3\sqrt{x-5}}{\sqrt{x+1}}\ge0\)
a : dfrac{sqrt{x}}{sqrt{x}+3}+dfrac{2sqrt{x}}{sqrt{x}-3}-dfrac{3x+9}{x-9}với x ≥ 0 x ≠ 9b : dfrac{3}{sqrt{x}-1}-dfrac{sqrt{x}+5}{x-1}với x ≥ 0 x ≠ 1c : left(dfrac{15-sqrt{x}}{x-25}+dfrac{2}{sqrt{x}+5}right):dfrac{sqrt{x}+1}{sqrt{x}-5}với x ≥ 0 x ≠ 0d : dfrac{3sqrt{x}+1}{x+2sqrt{x}-3}-dfrac{2}{sqrt{x}+3}với x ≥ 0 x ≠ 1
Đọc tiếp
a : \(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)với x ≥ 0 x ≠ 9
b : \(\dfrac{3}{\sqrt{x}-1}-\dfrac{\sqrt{x}+5}{x-1}\)với x ≥ 0 x ≠ 1
c : \(\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)với x ≥ 0 x ≠ 0
d : \(\dfrac{3\sqrt{x}+1}{x+2\sqrt{x}-3}-\dfrac{2}{\sqrt{x}+3}\)với x ≥ 0 x ≠ 1
a) \(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\left(x\ge0;x\ne0\right)\)
\(=\dfrac{\sqrt{x}.\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right).\left(\sqrt{x-3}\right)}+\dfrac{2\sqrt{x}.\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right).\left(\sqrt{x}+3\right)}-\dfrac{3x+9}{\left(\sqrt{x}-3\right).\left(\sqrt{x+3}\right)}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right).\left(\sqrt{x-3}\right)}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right).\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3.\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right).\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
Đúng 3
Bình luận (0)
b) \(\dfrac{3}{\sqrt{x}-1}-\dfrac{\sqrt{x}+5}{x-1}\left(x\ge0;x\ne1\right)\)
\(=\dfrac{3.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}+5}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}+3-\sqrt{x}-5}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}-2}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2.\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right).\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2}{\sqrt{x}+1}\)
Đúng 1
Bình luận (0)
c) \(\left(\dfrac{15-\sqrt{x}}{x-25}+\dfrac{2}{\sqrt{x}+5}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\left(x\ge0;x\ne1\right)\)
\(=\left(\dfrac{15-\sqrt{x}}{\left(\sqrt{x}-5\right).\left(\sqrt{x}+5\right)}+\dfrac{2.\left(\sqrt{x}-5\right)}{\left(\sqrt{x}-5\right).\left(\sqrt{x}+5\right)}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(=\dfrac{15-\sqrt{x}+2\sqrt{x}-10}{\left(\sqrt{x}-5\right).\left(\sqrt{x}+5\right)}:\dfrac{\sqrt{x}+1}{\sqrt{x}-5}\)
\(=\dfrac{\sqrt{x}+5}{\left(\sqrt{x}-5\right).\left(\sqrt{x}+5\right)}.\dfrac{\sqrt{x}-5}{\sqrt{x}+1}\)
\(\dfrac{1}{\sqrt{x}+1}\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
1, \(K=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\)
2, \(\sqrt{x-3}-2.\sqrt{x^2-3x}=0\)
3, \(\dfrac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\)
4, \(x-5\sqrt{x}+4=0\)
1,\(K=\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{x}}\)
\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{6-2\sqrt{5}}+\sqrt{6+2\sqrt{5}}\right)\)\(=\dfrac{1}{\sqrt{2}}\left(\sqrt{\left(\sqrt{5}-1\right)^2}+\sqrt{\left(\sqrt{5}+1\right)^2}\right)\)
\(=\dfrac{1}{\sqrt{2}}\left(\left|\sqrt{5}-1\right|+\sqrt{5}+1\right)\)\(=\dfrac{1}{\sqrt{2}}\left|\sqrt{5}-1+\sqrt{5}+1\right|=\dfrac{1}{\sqrt{2}}.2\sqrt{5}\)\(=\sqrt{10}\)
2, \(\sqrt{x-3}-2\sqrt{x^2-3x}=0\left(đk:x\ge3\right)\)
\(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\1-2\sqrt{x}=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=\left(\dfrac{1}{2}\right)^2=\dfrac{1}{4}\left(ktm\right)\end{matrix}\right.\)
Vậy pt có nghiệm x=3
3, \(\dfrac{9x-7}{\sqrt{7x+5}}=\sqrt{7x+5}\left(đk:x>-\dfrac{5}{7}\right)\)
\(\Leftrightarrow9x-7=7x+5\)
\(\Leftrightarrow x=6\left(tm\right)\)
4, \(x-5\sqrt{x}+4=0\)(đk: \(x\ge0\))
\(\Leftrightarrow\left(\sqrt{x}-1\right)\left(\sqrt{x}-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=1\\\sqrt{x}=4\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=16\end{matrix}\right.\) (tm)
Vậy...
Đúng 2
Bình luận (0)
1) Bạn tự làm
2) ĐK: \(x\ge3\)
PT \(\Leftrightarrow\sqrt{x-3}\left(1-2\sqrt{x}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x-3}=0\\2\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\left(loại\right)\end{matrix}\right.\)
Vậy ...
3) ĐK: \(x>-\dfrac{5}{7}\)
PT \(\Rightarrow9x-7=7x+5\) \(\Leftrightarrow x=6\)
Vậy ...
4) ĐK: \(x\ge0\)
PT \(\Leftrightarrow x-4\sqrt{x}-\sqrt{x}+4=0\)
\(\Leftrightarrow\left(\sqrt{x}-4\right)\left(\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=4\\\sqrt{x}=1\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=16\\x=1\end{matrix}\right.\)
Vậy ...
Đúng 1
Bình luận (0)
Giải phương trình :
a.\(x^2+5x^2-3=0\)
b.\(x^2-\left(2\sqrt{3}-1\right)x+4\sqrt{3}-6=0\)
c.\(x^2-6x+9=0\)
d.\(x^2-4\sqrt{3}x-4=0\)
c: \(\Leftrightarrow x-3=0\)
hay x=3
Đúng 1
Bình luận (0)