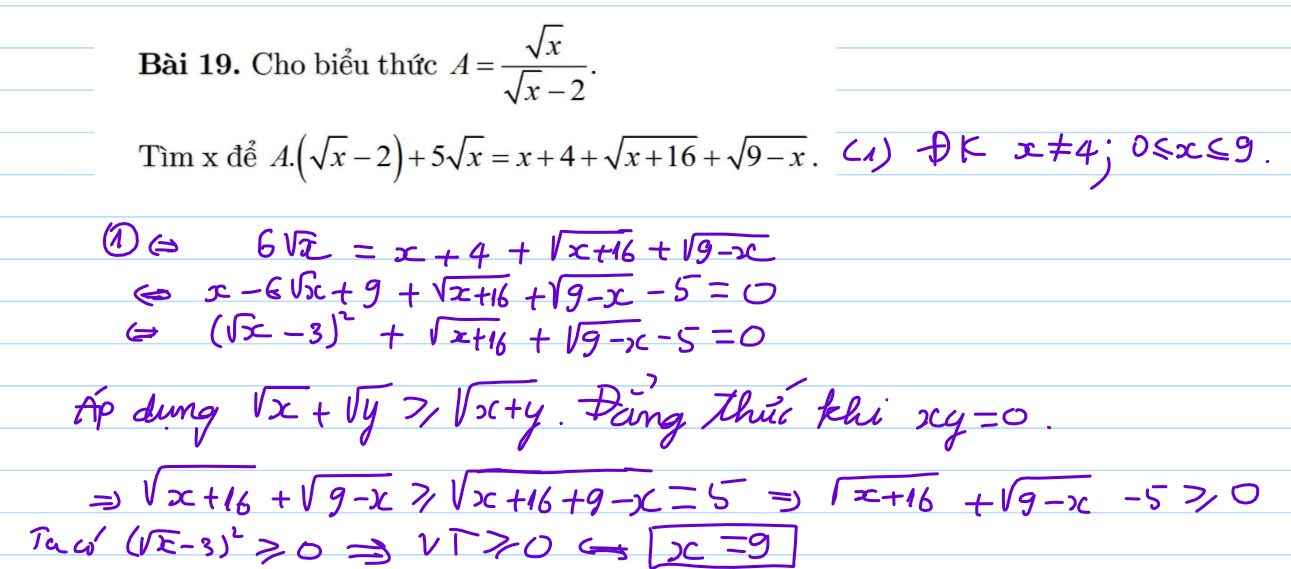Đáp án chi tiết

Cách số 2 

Cách số 2

1: Ta có: \(A=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)

\(=\dfrac{2\sqrt{x}-9-\left(x-9\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

Để \(A=-\dfrac{1}{\sqrt{x}}\) thì \(x+\sqrt{x}=-\sqrt{x}+3\)

\(\Leftrightarrow x+2\sqrt{x}-3=0\)

\(\Leftrightarrow\left(\sqrt{x}+3\right)\left(\sqrt{x}-1\right)=0\)

\(\Leftrightarrow x=1\left(nhận\right)\)

2: Để A nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-3\)

\(\Leftrightarrow\sqrt{x}-3\in\left\{-1;1;2;-2;4;-4\right\}\)

\(\Leftrightarrow\sqrt{x}\in\left\{2;4;5;1;7\right\}\)

\(\Leftrightarrow x\in\left\{16;25;1;49\right\}\)

1: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\notin\left\{4;9\right\}\end{matrix}\right.\)

Ta có: \(A=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(1,A=\dfrac{2\sqrt{x}-9-x+9+2x-3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ A=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ A=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\left(x\ge0;x\ne4;x\ne9\right)\\ 2,A< 1\Leftrightarrow\dfrac{\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}-3}< 0\\ \Leftrightarrow\dfrac{4}{\sqrt{x}-3}< 0\Leftrightarrow\sqrt{x}-3< 0\Leftrightarrow0\le x< 9\)

ĐKXĐ: x>0; x<>9

\(A=\left(\dfrac{-\left(\sqrt{x}+3\right)}{\sqrt{x}-3}+\dfrac{\sqrt{x}-3}{\sqrt{x}+3}-\dfrac{4x}{x-9}\right):\left(\dfrac{5\sqrt{x}-4\sqrt{x}-2}{\sqrt{x}\left(3-\sqrt{x}\right)}\right)\)

\(=\dfrac{-x-6\sqrt{x}-9+x-6\sqrt{x}+9-4x}{x-9}:\dfrac{-\sqrt{x}+2}{\sqrt{x}\left(\sqrt{x}-3\right)}\)

\(=\dfrac{-4x-12\sqrt{x}}{x-9}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{-\left(\sqrt{x}-2\right)}\)

\(=\dfrac{4x\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(x-9\right)\left(\sqrt{x}-2\right)}=\dfrac{4x}{\sqrt{x}-2}\)

|A|>-A

=>A>=0

=>4x>0

=>x>0 và x<>9

a) \(Q=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\left(x\ge0,x\ne4,9\right)\)

\(=\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

b) \(\sqrt{x}=\sqrt{6+4\sqrt{2}}=\sqrt{\left(2+\sqrt{2}\right)^2}=2+\sqrt{2}\)

\(\Rightarrow Q=\dfrac{2+\sqrt{2}+1}{2+\sqrt{2}-3}=\dfrac{3+\sqrt{2}}{\sqrt{2}-1}=\dfrac{\left(3+\sqrt{2}\right)\left(\sqrt{2}+1\right)}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}\)

\(=4\sqrt{2}+5\)

c) \(Q=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}=1+\dfrac{4}{\sqrt{x}-3}\)

Để \(Q\in Z\Rightarrow4⋮\sqrt{x}-3\Rightarrow\sqrt{x}-3\in\left\{1;2;4;-1;-2;-4\right\}\)

\(\Rightarrow\sqrt{x}\in\left\{4;5;7;2;1\right\}\Rightarrow x\in\left\{16;25;49;4;1\right\}\)

a) Ta có: \(Q=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\)

\(=\dfrac{2\sqrt{x}-9-\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)+\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{2\sqrt{x}-9-x+9+2x-4\sqrt{x}+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

b) Thay \(x=6+4\sqrt{2}\) vào Q, ta được:

\(Q=\dfrac{2+\sqrt{2}+1}{2+\sqrt{2}-3}=\dfrac{3+\sqrt{3}}{\sqrt{2}-1}=\left(3+\sqrt{3}\right)\left(\sqrt{2}+1\right)\)

a) Ta có: \(M=\left(1-\dfrac{x-3\sqrt{x}}{x-9}\right):\left(\dfrac{9-x}{x+\sqrt{x}-6}-\dfrac{\sqrt{x}-3}{2-\sqrt{x}}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\right)\)

\(=\left(1-\dfrac{x-3\sqrt{x}}{x-9}\right):\left(\dfrac{9-x}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)

\(=\left(1-\dfrac{x-3\sqrt{x}}{x-9}\right):\left(\dfrac{9-x+x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}-\dfrac{\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\right)\)

\(=\left(1-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right):\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{\sqrt{x}+3-\sqrt{x}}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}+3}{-\left(\sqrt{x}-2\right)}\)

\(=\dfrac{-3}{\sqrt{x}-2}\)

câu a tham khảo ở đây

https://hoc24.vn/cau-hoi/.1145652136620

b) \(x=25\Rightarrow P=\dfrac{\sqrt{25}+1}{\sqrt{25}-3}=\dfrac{6}{2}=3\)

c) \(A< 1\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}< 1\Rightarrow\dfrac{\sqrt{x}+1}{\sqrt{x}-3}-1< 0\Rightarrow\dfrac{4}{\sqrt{x}-3}< 0\)

mà \(4>0\Rightarrow\sqrt{x}-3< 0\Rightarrow\sqrt{x}< 3\Rightarrow x< 9\Rightarrow0\le x< 9,x\ne4\)

\(M=\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}+\dfrac{2\sqrt{x}+1}{3-\sqrt{x}}\left(\text{đ}k\text{x}\text{đ}:x\ge3\right)\\ =\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\sqrt{x}-2}-\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}\\ =\dfrac{2\sqrt{x}-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{x-9}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}-\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\\ =\dfrac{2\sqrt{x}-9-\left(x-9\right)-\left(2x-4\sqrt{x}+\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\)

\(=\dfrac{2\sqrt{x}-9-x+9-2x+4\sqrt{x}-\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{5\sqrt{x}-3x+2}{x-5\sqrt{x}+6}\)

__

Để \(M\in Z\) thì \(x-5\sqrt{x}+6\) thuộc ước của \(5\sqrt{x}-3x+2\)

\(\Rightarrow x-5\sqrt{x}+6=-5\sqrt{x}-3x+2\\ \Leftrightarrow x-5\sqrt{x}+6+5\sqrt{x}+3x-2=0\\ \Leftrightarrow4x-4=0\\ \Leftrightarrow4x=4\\ \Leftrightarrow x=1\)

(a) Với \(x\ge0,x\ne9\), ta có: \(A=\left(\dfrac{2}{\sqrt{x}-3}+\dfrac{1}{\sqrt{x}+3}\right):\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{2\left(\sqrt{x}+3\right)+\left(\sqrt{x}-3\right)}{x-9}:\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)

\(=\dfrac{3\left(\sqrt{x}+1\right)}{x-9}\cdot\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)

\(=\dfrac{3}{\sqrt{x}+3}.\)

(b) Ta có: \(x=7+4\sqrt{3}=\left(2+\sqrt{3}\right)^2\)

\(\Rightarrow\sqrt{x}=2+\sqrt{3}\).

Thay vào biểu thức \(A\) (thỏa mãn điều kiện), ta được: \(A=\dfrac{3}{2+\sqrt{3}+3}=\dfrac{3}{5+\sqrt{3}}\)

\(=\dfrac{3\left(5-\sqrt{3}\right)}{5^2-\left(\sqrt{3}\right)^2}=\dfrac{15-3\sqrt{3}}{22}.\)

(c) Để \(A=\dfrac{3}{5}\Rightarrow\dfrac{3}{\sqrt{x}+2}=\dfrac{3}{5}\)

\(\Rightarrow\sqrt{x}+2=5\Leftrightarrow x=9\) (không thỏa mãn).

Vậy: \(x\in\varnothing.\)

(d) Để \(A>1\Leftrightarrow A-1>0\Rightarrow\dfrac{3}{\sqrt{x}+3}-1>0\)

\(\Leftrightarrow\dfrac{1-\sqrt{x}}{\sqrt{x}+3}>0\Rightarrow1-\sqrt{x}>0\) (do \(\sqrt{x}+3>0\forall x\inĐKXĐ\))

\(\Rightarrow x< 1\). Kết hợp với điều kiện thì \(0\le x< 1.\)

(e) \(A\in Z\Rightarrow\dfrac{3}{\sqrt{x}+3}\in Z\Rightarrow\left(\sqrt{x}+3\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}+3=1\\\sqrt{x}+3=-1\\\sqrt{x}+3=3\\\sqrt{x}+3=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=-2\left(VL\right)\\\sqrt{x}=-4\left(VL\right)\\\sqrt{x}=0\Leftrightarrow x=0\left(TM\right)\\\sqrt{x}=-6\left(VL\right)\end{matrix}\right.\)

Vậy: \(x=0.\)