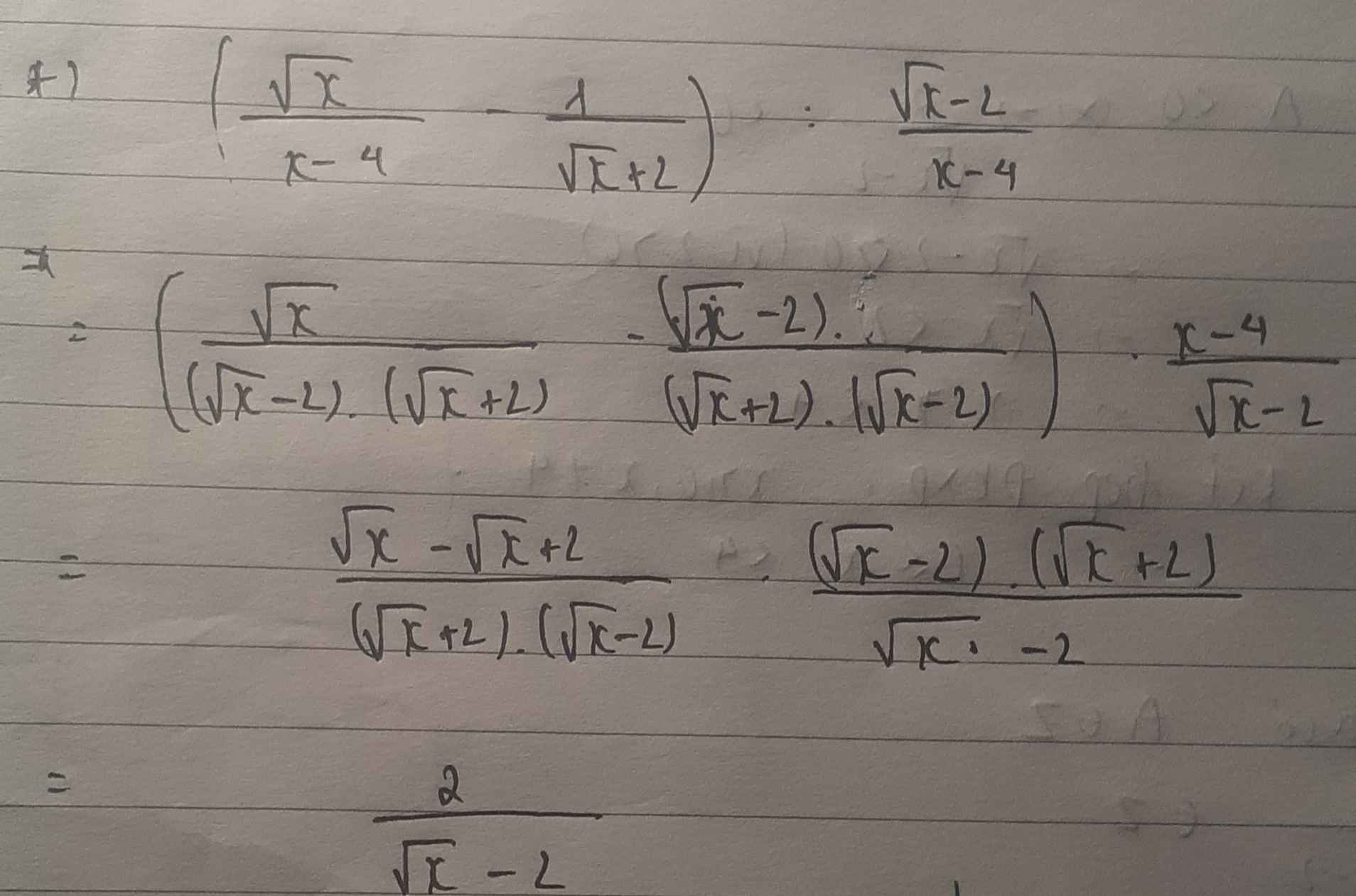Lời giải:
$M(2\sqrt{x}-3)=\sqrt{x}+2$

$\Leftrightarrow \sqrt{x}(2M-1)=3M-2$

$\Leftrightarrow x=(\frac{3M-2}{2M-1})^2$

Vì $x$ nguyên nên $\frac{3M-2}{2M-1}$ nguyên 

$\Rightarrow 3M-2\vdots 2M-1$

$\Leftrightarrow 6M-4\vdots 2M-1$
$\Leftrightarrow 3(2M-1)-1\vdots 2M-1$
$\Leftrightarrow 1\vdots 2M-1$

$\Rightarrow 2M-1\in\left\{\pm 1\right\}$

$\Rightarrow M=0;1$

$\Leftrightarrow x=4; 1$ (đều tm)

Biểu thức gì vậy bạn?

tìm các giá trị nguyên của x để biểu thức P=A.B  nhận giá trị nguyên

Để M là số nguyên thì \(12\sqrt{x}+5⋮3\sqrt{x}-1\)

=>\(12\sqrt{x}-4+9⋮3\sqrt{x}-1\)

=>\(3\sqrt{x}-1\in\left\{1;-1;3;-3;9;-9\right\}\)

=>\(3\sqrt{x}\in\left\{2;0;4;10\right\}\)

=>\(\sqrt{x}\in\left\{0;\dfrac{2}{3};\dfrac{4}{3};\dfrac{10}{3}\right\}\)

mà x là số chính phương

nên x=0

\(M=\dfrac{12\sqrt{x}+5}{3\sqrt{x}-1}\)

\(M=\dfrac{12\sqrt{x}-4+9}{3\sqrt{x}-1}\)

\(M=\dfrac{4\left(3\sqrt{x}-1\right)+9}{3\sqrt{x}-1}\)

\(M=\dfrac{4\left(3\sqrt{x}-1\right)}{3\sqrt{x}-1}+\dfrac{9}{3\sqrt{x}-1}\)

\(M=4+\dfrac{9}{3\sqrt{x}-1}\)

M nguyên khi: 

\(9\) ⋮ \(3\sqrt{x}-1\)

Mà: \(3\sqrt{x}-1\ge-1\)

\(\Rightarrow3\sqrt{x}-1\in\left\{1;-1;3;9\right\}\)

\(\Rightarrow\sqrt{x}\in\left\{\dfrac{2}{3};0;\dfrac{4}{3};\dfrac{10}{3}\right\}\)

\(\Rightarrow x\in\left\{\dfrac{4}{9};0;\dfrac{16}{9};\dfrac{100}{9}\right\}\)

Mà: x là số chính phương nên:

x = 0

a: Ta có: \(N=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)

\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)

\(=x-\sqrt{x}+1\)

a: \(P=\left(\dfrac{2+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}\)

\(=\dfrac{1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)

b: Để P nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)

\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)

hay \(x\in\left\{0;4;9\right\}\)

Lời giải:

$M=\frac{2(\sqrt{x}-3)+7}{\sqrt{x}-3}=2+\frac{7}{\sqrt{x}-3}$

Để $M$ nguyên thì $\frac{7}{\sqrt{x}-3}$

Với $x$ nguyên không âm thì điều này xảy ra khi mà $\sqrt{x}-3$ là ước của $7$

$\Rightarrow \sqrt{x}-3\in\left\{\pm 1; \pm 7\right\}$

$\Rightarrow \sqrt{x}\in \left\{4; 2; 10; -4\right\}$

Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}\in \left\{4; 2; 10\right\}$

$\Rightarrow x\in \left\{16; 4; 100\right\}$ (tm)

\(P=A\cdot B\)

\(=\dfrac{2\sqrt{x}}{\sqrt{x}-3}\cdot\dfrac{2\sqrt{x}+6+x-3\sqrt{x}+3-5\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}-3\right)}\cdot\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)

\(=\dfrac{2\sqrt{x}}{\left(\sqrt{x}+3\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}-3\right)^2}=\dfrac{2\sqrt{x}}{\sqrt{x}+3}\)

Để P nguyên thì 

\(2\sqrt{x}⋮\sqrt{x}+3\)

\(\Leftrightarrow2\sqrt{x}+6-6⋮\sqrt{x}+3\)

=>\(\sqrt{x}+3\inƯ\left(-6\right)\)

=>\(\sqrt{x}+3\in\left\{3;6\right\}\)

=>\(\sqrt{x}\in\left\{0;3\right\}\)

=>\(x\in\left\{0;9\right\}\)

Kết hợp ĐKXĐ, ta được: x=0

ĐKXĐ: x>=0

Để A là số nguyên thì \(\sqrt{x}+13⋮\sqrt{x}+5\)

=>\(\sqrt{x}+5+8⋮\sqrt{x}+5\)

=>\(\sqrt{x}+5\inƯ\left(8\right)\)

mà \(\sqrt{x}+5>=5\)

nên \(\sqrt{x}+5=8\)

=>x=9

ĐK: \(x\ge0\) 

Để \(\dfrac{\sqrt{x}+13}{\sqrt{x}+5}\) có giá trị nguyên 

Mà:  \(\dfrac{\sqrt{x}+13}{\sqrt{x}+5}=\dfrac{\sqrt{x}+5+8}{\sqrt{x}+5}\)

\(=\dfrac{\sqrt{x}+5}{\sqrt{x}+5}+\dfrac{8}{\sqrt{x}+5}=1+\dfrac{8}{\sqrt{x}+5}\)

Vậy:  \(8\) ⋮ \(\sqrt{x}+5\)

\(\Rightarrow\sqrt{x}+5\inƯ\left(8\right)=\left\{1;-1;2;-2;4;-4;8;-8\right\}\)

Mà: \(\sqrt{x}+5\ge5\)

\(\Rightarrow\sqrt{x}+5\in\left\{8\right\}\)

\(\Rightarrow x=9\left(tm\right)\)

\(P\in Z\Rightarrow3P\in Z\Rightarrow\dfrac{3\sqrt{x}+15}{3\sqrt{x}+1}\in Z\)

\(\Rightarrow1+\dfrac{14}{3\sqrt{x}+1}\in Z\)

\(\Rightarrow3\sqrt{x}+1=Ư\left(14\right)=\left\{1;2;7;14\right\}\) (do \(3\sqrt{x}+1\ge1\))

\(3\sqrt{x}+1=1\Rightarrow x=0\)

\(3\sqrt{x}+1=2\Rightarrow x=\dfrac{1}{9}\notin Z\) (loại)

\(3\sqrt{x}+1=7\Rightarrow x=4\)

\(3\sqrt{x}+1=14\Rightarrow x=\dfrac{169}{9}\notin Z\) (loại)

Thế \(x=\left\{0;4\right\}\) vào P đều thỏa mãn

Vậy ....