Cho a, b, c thuộc đoạn [0;1]. CMR;
\(\dfrac{a}{1+b+ac}+\dfrac{b}{1+c+ab}+\dfrac{c}{1+a+bc}\le1\)
Những câu hỏi liên quan
Cho các số thực a, b, c (với
a
≠
0
sao cho: phương trình
a
x
2
+
b
x
+
c
0
có hai nghiệm thuộc đoạn [0;1]. Tìm giá trị lớn nhất của biểu thức: A. 1 B. 3 C. 4 D. 5
Đọc tiếp
Cho các số thực a, b, c (với a ≠ 0 sao cho: phương trình a x 2 + b x + c = 0 có hai nghiệm thuộc đoạn [0;1]. Tìm giá trị lớn nhất của biểu thức:
A. 1
B. 3
C. 4
D. 5
cho tam giác ABC vuông tại A, AH là đường cao . Gọi M là điểm thuộc đoạn HC. E,K lần lượt là hình chiếu của B,C trên AM, biết H(2;2), K(3;1) , A thuộc d1: 2x-y-2=0; E thuộc d2:x+y-6=0. Tìm tọa độ A,B,C
cho tam giác ABC vuông tại A, AH là đường cao . Gọi M là điểm thuộc đoạn HC. E,K lần lượt là hình chiếu của B,C trên AM, biết H(2;2), K(3;1) , A thuộc d1: 2x-y-2=0; E thuộc d2:x+y-6=0. Tìm tọa độ A,B,C
Ta thấy ^EHK = ^EHM + ^KHM = ^BAE + ^CAM = ^BAC = 900
Đường thẳng HE: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HK}\left(1;-1\right)\Rightarrow\) \(HE:x-y=0\)
Xét hệ \(\hept{\begin{cases}x-y=0\\x+y-6=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=3\end{cases}}}\Rightarrow E\left(3;3\right)\)
Đường thẳng KE: đi qua \(K\left(3;1\right)\), VTCP \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KE:\hept{\begin{cases}x=3\\y=1+2t\end{cases}}\)
Xét hệ \(\hept{\begin{cases}2x-y-2=0\\x=3\\y=1+2t\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=4\end{cases}}\Rightarrow A\left(3;4\right)\)
Đường thẳng BC: đi qua \(H\left(2;2\right)\), VTPT \(\overrightarrow{HA}\left(1;2\right)\Rightarrow BC:x+2y-6=0\)(1)
Đường thẳng EB: đi qua \(E\left(3;3\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow BE:y=3\)(2)
Đường thẳng KC: đi qua \(K\left(3;1\right)\), VTPT \(\overrightarrow{KE}\left(0;2\right)\Rightarrow KC:y=1\) (3)
Từ (1);(2) suy ra \(B\left(0;3\right)\), từ (1);(3) suy ra \(C\left(4;1\right)\)
Vậy \(A\left(3;4\right),B\left(0;3\right),C\left(4;1\right).\)
Cho hai điểm A,B thuộc đồ thị hàm số ysinx trên đoạn
0
;
π
,
các điểm C,D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và
C
D
2
π
3
.Độ dài đoạn thẳng BC bằng A....
Đọc tiếp
Cho hai điểm A,B thuộc đồ thị hàm số y=sinx trên đoạn 0 ; π , các điểm C,D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và C D = 2 π 3 .
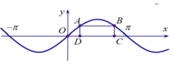
Độ dài đoạn thẳng BC bằng
A. 2 2 .
B. 1 2 .
C.1
D. 3 2 .
Cho hai điểm A, B thuộc đồ thị hàm số ysinx trên đoạn
0
;
π
các điểm C, D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và CD
2
π
3
Độ dài đoạn thẳng BC bằng A.
2
2
B.
1
2
C. 1 D.
-...
Đọc tiếp
Cho hai điểm A, B thuộc đồ thị hàm số y=sinx trên đoạn 0 ; π các điểm C, D thuộc trục Ox sao cho tứ giác ABCD là hình chữ nhật và CD = 2 π 3
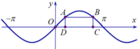
Độ dài đoạn thẳng BC bằng
A. 2 2
B. 1 2
C. 1
D. - 2 2
Cho A(3;0;0); B(0;-3;0); C(0;0;3). Tìm tọa độ điểm H thuộc mặt phẳng (ABC) sao cho đoạn OH có độ dài ngắn nhất.
Đọc tiếp
Cho A(3;0;0); B(0;-3;0); C(0;0;3). Tìm tọa độ điểm H thuộc mặt phẳng (ABC) sao cho đoạn OH có độ dài ngắn nhất.
Cho a,b,c là các số thuộc đoạn [ -1;2 ] thõa mãn \(a^2+b^2+c^2=6.\) CMR : \(a+b+c>0\)
\(-1\le a;b;c\le2\)
\(\Rightarrow\left(a+1\right)\left(a-2\right)\le0\)
\(\Leftrightarrow a^2-a-2\le0\)
\(\Rightarrow a^2-2\le a\)
Tương tự ta có: \(b^2-2\le b\) ; \(c^2-2\le c\)
\(\Rightarrow a+b+c\ge a^2+b^2+c^2-6=0\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(-1;-1;2\right)\) và cách hoán vị
Cho a,b,c,d,e thay đổi thuộc đoạn [-1;1] và a+b+c+d=0. tìm max \(a^2+b^2+c^2+d^2+e^2\)
Lời giải:
Vì \(a,b,c,d,e\in [-1;1]\Rightarrow \left\{\begin{matrix} a^2\leq |a|\\ b^2\leq |b|\\ c^2\leq |c|\\ d^2\leq |d|\\ e^2\leq |e|\\ |d|; |e|\leq 1\end{matrix}\right.\)
\(\Rightarrow a^2+b^2+c^2+d^2+e^2\leq |a|+|b|+|c|+|d|+|e|(*)\)
Có $5$ số nên theo nguyên lý Dirichlet thì tồn tại ít nhất \(\left[\frac{5}{2}\right]+1=3\) số cùng dấu. Giả sử đó là $a,b,c$
Khi đó \(ab\geq 0; c(a+b)\geq 0\)
\(\Rightarrow |a|+|b|+|c|=|a+b|+|c|=|a+b+c|\)
\(\Rightarrow |a|+|b|+|c|+|d|+|e|=|a+b+c|+|d|+|e|\)
\(=|-(d+e)|+|d|+|e|=|d+e|+|d|+|e|\)
\(\leq |d|+|e|+|d|+|e|\leq 1+1+1+1=4(**)\)
Từ \((*);(**)\Rightarrow a^2+b^2+c^2+d^2+e^2\leq 4\) hay max của biểu thức bằng $4$
Dấu "=" xảy ra khi \((a,b,c,d,e)=(1,1,0,-1,-1)\) và hoán vị.
Đúng 0
Bình luận (0)
Đúng 0
Bình luận (0)
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn
f
(
x
)
.
f
(
a
-
x
)
1...
Đọc tiếp
Cho f(x) là hàm liên tục trên đoạn [0;a] thỏa mãn f ( x ) . f ( a - x ) = 1 f ( x ) > 0 ; ∀ x ∈ [ 0 ; a ] và ∫ 0 a d x 1 + f ( x ) = b a c , trong đó b, c là hai số nguyên dương và b/c là phân số tối giản. Khi đó b+c có giá trị thuộc khoảng nào dưới đây?
A. (11;22)
B. (0;9)
C. (7;21)
D. (2017;2020)
Cho đoạn thẳng AB = 5cm, lấy điểm C nằm giữa A và B sao cho AC = 2cm. Vẽ điểm N không thuộc đoạn AB.
a,Vẽ tia AN, đoạn thẳng NC, đường thẳng NB. Kể tên các đoạn thẳng trong hình.
b,Tính độ dài đoạn thẳng CB.