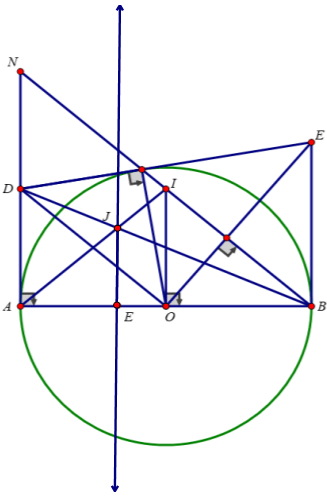
(3,5 điểm) Cho đường tròn (O; R) và điểm A cố định thuộc đường tròn. Trên tiếp tuyến với (O) tại A lấy một điểm K cố định. Một đường thẳng d thay đổi đi qua K và không đi qua tâm O cắt (O) tại điểm B và C (B nằm giữa C và K), Gọi M là trung điểm của BC.
1) Chứng minh bốn điểm A, O, M, K cùng thuộc một đường tròn.
2) Vẽ đường kính AN của đường tròn (O). Đường thẳng qua A và vuông góc với BC cắt MN tại H. Chứng minh tứ giác BHCN là hình bình hành.
3) Chứng minh H là trực tâm tam giác ABC
4) Khi đường thẳng d thay đổi và thỏa mãn điều kiện của đề bài, điểm H di động trên đường nào
Giúp mình với ạ!