Cho tam giác ABC có góc A bằng 90 độ, trên cạnh BC lấy điểm E sao cho BE=BA. Tia phân giác của góc B cắt AC ở D. Trên tia đối của AB lấy điểm K sao cho AK=EC.
a, CMR: ba điem K,D,E thẳng hàng
b, Kéo dài đường thẳng DE cắt AB tại K. CMR AK=EC
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
b) Ta có: ΔABD=ΔEBD(cmt)
nên \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BED}=90^0\)
Cho tam giác ABC có Góc A = 90 độ, trên cạnh BC lấy điểm E sao cho BE = BA. Tia phan giác của góc B cắt AC ở D.
a) So sánh độ dài DA và DE
b) tính số đo gó \c BED
c) Chứng minh BD là đường trung trực của đoạn thẳng AE
d) Trên tia đối của tia AB lấy điểm K sao cho AK = AB. CHứng minh CA là tia phân giác của góc BCK
Cho tam giác ABC có góc A = 90°, trên cạnh BC lấy điểm E sao cho BE = BA. Tia phân giác của góc B cắt AC ở D. Kéo dài ED cắt tia BA tại K. a) Cho BC = 10 cm, AB = 6cm. Hãy tính AC. b) Chứng minh : DA = DE. c) Chúng minh rằng: tam giác DKC là tam giác cân.
a: AC=8cm
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
a, Xét tg ABD và tg EBD có :
AB = EB (gt)
gABD = gEBD (BD là tia phân giác của gABE)
BD chung
=> tgABD = tgEBD (c.g.c)
=> DA = DE ( hai cạnh tương ứng )
b,vì tgABD = tgEBD (cmt)
=>gABD = gAEB=90 độ (hai góc tương ứng)
=>gDAK = gDEC = 90 độ
xét tgAKD và tgEDC có:
gDAK = gDEC (cmt)
AD = DE ( cmt)
gADK = gEDC ( hai góc đối đỉnh)
=> tgAKD = tgEDC (g.c.g)
=> DK = DC (hai cạnh tương ứng)
=> tg DKC cân tại D
c,xét tgABC vuông tại A ( góc A = 90độ , theo định lí Pytago ta có
BC^2=AB^2 + AC^2
=>AC^2 = 100- 36=64
=> AC = 8 (cm)
Cho tam giác ABC có AB < AC. Tia phân giác góc A cắt cạnh BC tại D. Lấy điểm E trên cạnh AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm F sao cho BF = EC. Chứng minh rằng :
a) DB = DE
b) tam giác BDF= tam giác EDC
c) E, D, F thẳng hàng
a: Xét ΔABD và ΔAED có
AB=AE
góc BAD=góc EAD
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
b: Xét ΔDBF và ΔDEC có
góc DBF=góc DEC
DB=DE
góc BDF=góc EDC
Do đo: ΔDBF=ΔDEC
c:ΔDBF=ΔDEC
nên góc BDF=góc EDC
=>góc BDF+góc BDE=180 độ
=>E,D,F thẳng hàng
cho tam giác abc vuông tại a có góc b= 57 đọ tia phân giác bd của góc abc cát ac tại d trên bc lấy điểm e sao cho ba=be trên tia đối tia ab lấy điểm i sao cho ai=ec
chứng minh i,d,e thẳng hàng
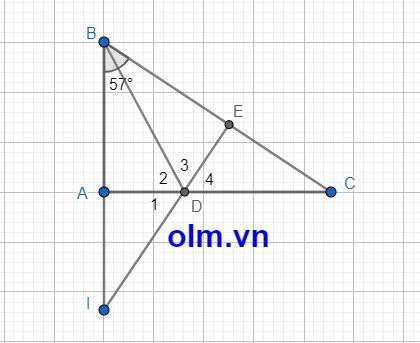
Xét tam giác ABD và tam giác EBD có
\(\widehat{ABD}\) = \(\widehat{EBD}\) (gt)
AB = BE (gt)
BD chung
⇒\(\Delta\)ABD = \(\Delta\) EBD (c-g-c)
⇒AD = DE
⇒ \(\widehat{BAD}\) = \(\widehat{BED}\) = 900
\(\widehat{DEC}\) = 1800 - 900 = 900
Xét tam giác ADI và tam giác EDC có:
\(\widehat{DAI}\) = \(\widehat{DEC}\) = 900 (cmt)
AD = DE (cmt)
AI = EC (gt)
⇒ \(\Delta\)ADI = \(\Delta\)EDC (c-g-c)
⇒ D1 = D4
Mà D2 + D3 + D4 = 1800
⇒ D1 + D2 + D3 = 1800
⇒ \(\widehat{IDE}\) = 1800
⇒ I;D;E thẳng hàng (đpcm)
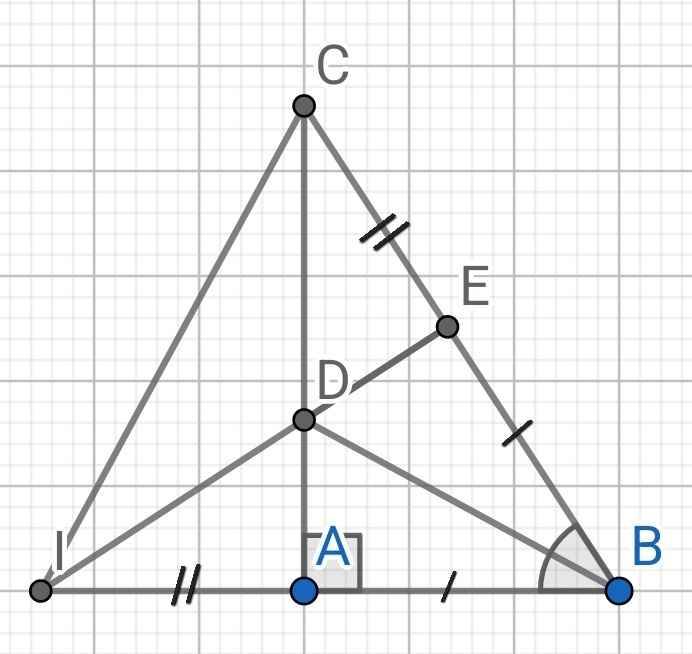 Do BD là tia phân giác của ∠ABC (gt)
Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠EBD
Xét ∆ABD và ∆EBD có:
AB = BE (gt)
∠ABD = ∠EBD (cmt)
BD là cạnh chung
⇒ ∆ABD = ∆EBD (c-g-c)
⇒ ∠BAD = ∠BED = 90⁰ (hai góc tương ứng)
⇒ DE ⊥ BC
Do AI = EC (gt)
AB = BE (gt)
⇒ BI = AI + AB = BE + EC = BC
∆BCI có:
BI = BC (cmt)
⇒ ∆BCI cân tại B
Mà BD là tia phân giác của ∠ABC
⇒ BD là tia phân giác của ∠IBC
⇒ BD là đường cao của ∆BCI
Lại có:
CA ⊥ AB (∆ABC vuông tại A)
CA ⊥ BI
⇒ CA là đường cao thứ hai của ∆BCI
⇒ ID là đường cao thứ ba của ∆BCI
⇒ ID ⊥ BC
Mà DE ⊥ BC (cmt)
⇒ I, D, E thẳng hàng
Cho tam giác ABC vuông tại A(AB<AC). Trên cạnh BC lấy D sao cho BD=BA. Vẽ tia phân giác góc ABC cắt AC tại I.
a)C/m Tam giác BAI= tam giác BDI
b) Trên tia đối của tia AB lấy điểm E sao cho BE=BC, tia BI cắt EC tại M
c) C/m: 3 điểm E,I,D thẳng hàng
Bài 6 : Cho tam giác ABC có góc BAC = 90o, trên cạnh BC lấy điểm E sao cho BE=BA . Tia phân giác của góc ABC cắt AC ở D.
a. So sánh các độ dài DA và DE
b. Tính số đo góc BED
c. Trên tia đối của tia AB lấy điểm F sao cho AF=CE
Chứng minh ba điểm E,D,F thẳng hàng
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
AD=ED
AF=EC
Do đó: ΔADF=ΔEDC
Suy ra: \(\widehat{ADF}=\widehat{EDC}\)
=>\(\widehat{ADF}+\widehat{ADE}=180^0\)
=>E,F,D thẳng hàng
Bài 6 : Cho tam giác ABC có góc BAC = 90o, trên cạnh BC lấy điểm E sao cho BE=BA . Tia phân giác của góc ABC cắt AC ở D.
a. So sánh các độ dài DA và DE
b. Tính số đo góc BED
c. Trên tia đối của tia AB lấy điểm F sao cho AF=CE . Chứng minh ba điểm E,D,F thẳng hàng
a) Xét ΔADB và ΔEDB có:
BA = BE ( giả thiết )
Góc ABD = EBD ( BD là tia phân giác của góc ABE )
BD cạnh chung.
=> ΔADB = ΔEDB ( c.g.c )
=> DA = DE ( 2 cạnh tương ứng )
b) Vì ΔADB = ΔEDB nên góc DAB = DEB = 90 độ ( 2 góc tương ứng).
Mk vẽ hình ko đc đẹp cho lắm, thông cảm nha!
Bài 1:
Cho góc nhọn xAy, trên tia Ax lấy điểm B, trên tia Ay lấy điểm C sao cho AB = AC. Gọi M là trung điểm của BC và E là trung điểm của AC, trên tia đối của tia EM lấy điểm H sao cho EH = EM
a) Chứng minh ( CM ) : tam giác ABM = tam giác ACM
b) CM : AM vuông góc BC
c) CM : tam giác AEH = tam giác CEM
d) Gọi D là trung điểm của AB. Từ B vẽ đường thẳng song song với AM, đường thẳng này cắt tia MD tại K. CM : ba điểm H, A, K thẳng hàng
Bài 2:
Cho tam giác ABC có góc B < 90 độ. Trên nửa mặt phẳng bờ BC chứa điểm A vẽ tia Bx khác BC, trên tia Bx lấy điểm D sao cho BD = BC. Trên nửa mặt phẳng bờ AB chứa điểm C vẽ tia By vuông góc với BA, trên tia By lấy E sao cho BE = BA
a) CMR : DA = EC
b) DA vuông góc EC
Bài 3:
Cho tam giác ABC vuông tại B và AC = 2AB. Kẻ phân giác AE ( E thuộc BC ) của góc A
a) CM : EA = EC
b) Tính góc A và góc C của tam giác ABC
GIÚP TỚ VỚI Ạ. TỚ ĐANG CẦN!!
Bài 1:
a) Xét tam giác ABM và tam giác ACM : AB=AC,AM chung ,BM=MC(vì M là trung điểm của BC gt)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
b) Tam giác ABC có AB=AC nên tam giác ABC cân tại A
=> đường trung tuyến AM đồng thời là đường cao
Vậy AM vuông góc BC
c) Xét tam giác AEH và tam giác CEM : AE=EC,EH=EM,\(\widehat{AEH}=\widehat{CEM}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta AEH=\Delta CEM\left(c.gc\right)\)
d) Ta có KB//AM(vì vuông góc với BM
\(\Rightarrow\widehat{KBD}=\widehat{DAM}\)(2 góc ở vị trí so le trong)
Xét tam giác KDB và MDA (2 góc đối đỉnh)
\(\Rightarrow\Delta KDB=\Delta DAM\left(g.c.g\right)\)
\(\Rightarrow KD=DM\left(1\right)\)
Tam giác ABM vuông tại M có trung tuyến MD
Nên : MD=BD=AD(2)
Từ (1) và (2) ta có : KD=DM=DB=AD
Tam giác KAM có trung tuyến ứng với cạnh KM là \(AD=\frac{AM}{2}\)
Nên : Tam giác KAM vuông tại A
Tương tự : Tam giác MAH vuông tại A
Ta có: Qua1 điểm A thuộc AM có 2 đường KA và AH cùng vuông góc với AM
Nên : K,A,H thẳng thàng
Bài 2 :
a) Ta có tam giác DAB=tam giác CEB(c.g.c)
Do : DA=CB(gt)
BE=BA(gt)
\(\widehat{DBA}=\widehat{CBE}\)(Cùng phụ \(\widehat{ABC}\))
=> DA=EC
b) Do tam giác DAB=tam giác CEB(ở câu a)
=> \(\widehat{BDA}=\widehat{BCE}\Rightarrow\widehat{BDA}+\widehat{BCD}=\widehat{BCE}+\widehat{BCD}\)
Mà : \(\widehat{BDA}+\widehat{BCD}=90^0\)( Do Bx vuông góc BC)
=> \(\widehat{BCE}+\widehat{BCD}=90^0\)
=> DA vuông góc với EC