\(y=\left|sinx-\left(1-2sin^2x\right)\right|=\left|2sin^2x+sinx-1\right|\)

Đặt \(t=sinx;-1\le t\le1\)

\(\Rightarrow y=\left|2t^2+t-1\right|\)

Đặt \(f\left(t\right)=2t^2+t-1;-1\le t\le1\)

Vẽ BBT của \(f\left(t\right)=2t^2+t-1;-1\le t\le1\) sẽ tìm được \(f\left(t\right)_{min}=-\dfrac{9}{8};f\left(t\right)_{max}=2\)

\(\Rightarrow0\le\left|f\left(t\right)\right|\le2\)

\(\Leftrightarrow0\le y\le2\)

\(\Rightarrow y_{min}=0\Leftrightarrow2sin^2x+sinx-1=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)

\(y_{max}=2\Leftrightarrow t=1\Leftrightarrow sinx=1\)

\(A^2=\left(\sqrt{2}.\sqrt{2}x+\sqrt{3}.\sqrt{3}y\right)^2\)

\(\Rightarrow A^2\le\left(2+3\right)\left(2x^2+3y^2\right)\le5.5=25\)

\(\Rightarrow-5\le A\le5\)

\(A_{max}=5\) khi \(x=y=1\)

\(A_{min}=-5\) khi \(x=y=-1\)

a)đặt A=\(x^2+5y^2-2xy+4y+3\)

 \(=\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)+2\)

=\(=\left(x-y\right)^2+\left(2y+1\right)^2+2\)

ta thấy GTNN của A =2 khi x=y=-1/2

Bmin =100

Cmin=90

Dmin =120

Mấy ngày rồi chắc bạn làm được .

A = 2² - 20\(x\) + 2024 

A = 4 + 2024  - 20\(x\)

A = 2028 - 20\(x\) 

Ta có đồ thị 

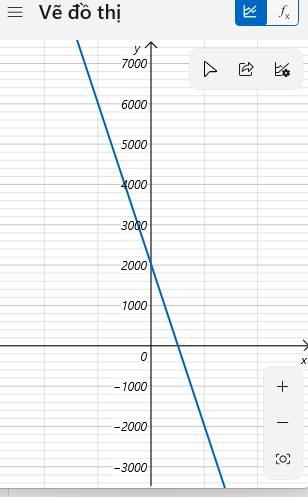
Không có giá trị nhỏ nhất em nhá