Cho x2 + y2 = 1. Tìm min S, max S biết S= x6 + y6

Những câu hỏi liên quan
Cho x và y là 2 số thực thỏa mãn : x2 + y2 = 1
Tìm giá trị bé nhất của biểu thức P = x6 + y6
P = x6 + y6 = (x2 + y2)(x4 - x2 y2 + y4)
= (x2 + y2)2 - 3x2 y2 \(\ge1-3×\frac{\left(x^2+y^2\right)^2}{4}=1-\frac{3}{4}=\frac{1}{4}\)
Đạt được khi x2 = y2 = \(\frac{1}{2}\)
Đúng 0
Bình luận (0)
làm ra (x^2+y^2)^2-3.x^2.y^2 rùi ko bt
Đúng 0
Bình luận (0)
Cho x2+y2+xy=3.Tìm Min và Max M=x2+y2-xy
giúp với mấy b.n!\
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow M\le9\)
\(M_{max}=9\) khi \(\left\{{}\begin{matrix}x+y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{\dfrac{1}{3}\left(x^2+y^2+xy\right)+\dfrac{2}{3}\left(x^2+y^2-2xy\right)}{x^2+y^2+xy}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\)
\(\Rightarrow M\ge1\)
\(M_{min}=1\) khi \(\left\{{}\begin{matrix}x-y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow x=y=\pm1\)
Đúng 4
Bình luận (0)
cho x;yϵR thỏa mãn x2+y2-xy=4 tìm max và min của C=x2+y2
\(\dfrac{x^2+y^2}{2}\ge xy\Rightarrow-xy\ge-\dfrac{x^2+y^2}{2}\)
\(\Rightarrow4=x^2+y^2-xy\ge x^2+y^2-\dfrac{x^2+y^2}{2}=\dfrac{x^2+y^2}{2}\)
\(\Rightarrow x^2+y^2\le8\)
\(C_{max}=8\) khi \(x=y=\pm2\)
\(x^2+y^2\ge-2xy\Rightarrow-xy\le\dfrac{x^2+y^2}{2}\)
\(4=x^2+y^2-xy\le x^2+y^2+\dfrac{x^2+y^2}{2}=\dfrac{3}{2}\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\dfrac{8}{3}\)
\(C_{min}=\dfrac{8}{3}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}}\right);\left(\dfrac{2}{\sqrt{3}};-\dfrac{2}{\sqrt{3}}\right)\)
Đúng 1
Bình luận (1)
 Đúng thì like giúp mik nha bạn. Thx bạn
Đúng thì like giúp mik nha bạn. Thx bạn
Đúng 1
Bình luận (0)
cho x;y thỏa mãn x2+8/x2+y2/8=8 tìm max và min củaB=xy+2024
đúng thì like giúp mik nha bạn. Thx bạn
Đúng 4
Bình luận (5)
1: Tìm max: S -(3x-2)^2-(3x-1)^2 2: S-x^2-3y^2-2xy+10x+18y+82: tìm min max: P6x-8/x^2+93: tìm max : S-x^2+4x+1/2x^2+64 tìm min A x^6+512/x^2+85 tìm min A 2x^16x+41/x^2-8x+226 tìm min A x^2-4x+1/x^27 tìm max A x/(x+10)^28 cho x+y1, x,y0 tìm min A1/x+1/yMọi người ơi giải giuos mình với chiều nay mình hk r mà chưa bt cách giải làm sao mn giúp mình với ai đúng mình sẽ tích cho nhé ngay và luôn luôn. Cảm ơn mn nhiều
Đọc tiếp
1: Tìm max: S= -(3x-2)^2-(3x-1)^2
2: S=-x^2-3y^2-2xy+10x+18y+8
2: tìm min max: P=6x-8/x^2+9
3: tìm max : S=-x^2+4x+1/2x^2+6
4 tìm min A= x^6+512/x^2+8
5 tìm min A= 2x^16x+41/x^2-8x+22
6 tìm min A= x^2-4x+1/x^2
7 tìm max A= x/(x+10)^2
8 cho x+y=1, x,y>0 tìm min A=1/x+1/y
Mọi người ơi giải giuos mình với chiều nay mình hk r mà chưa bt cách giải làm sao mn giúp mình với ai đúng mình sẽ tích cho nhé ngay và luôn luôn. Cảm ơn mn nhiều
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
1. Cho 1 vật dao động điều hòa theo pt: X= 10cos( 10π T + T/3 )
a) Tìm Smax , Smin trong khoảng thời gian 1/30s ; 1/20s ; 1/15s ; 7/6s ; 11,125s ; 8,79s
b) Tìm Tmax , Tmin vật đi được quãng đường S= 10s ; 15s ; 10căn 2s ; 8s
MỌNG MỌI NGƯỜI GIÚP MIK Ạ
Hướng dẫn:
+ Trong nửa chu kì, quãng đường vật đi được luôn là 2A.
+ Trong thời gian t < T/2, quãng đường lớn nhất khi vật đi quanh VTCB (vì tốc độ trung bình ở đây lớn nhất), còn quãng đường nhỏ nhất khi vật đi quanh biên.
+ Tương tự, thời gian nhỏ nhất khi vật đi quanh VTCB, thời gian lớn nhất khi vật đi quanh biên.
Theo quy tắc đó bạn tự tìm ra lời giải nhé.
Đúng 0
Bình luận (1)
Biết x2+4y2+9z2=3 Tìm GTLN của S=2x+4y+6x
Cho x;y ∈ 𝑅 thỏa mãn x2+y2 -xy=4 . Tìm giá trị lớn nhất và nhỏ nhất của C= x2+y2
a) Áp dụng bất đẳng thức Cosi ta có :
\(x^2+1\geq 2x\\ 4y^2+1\geq 4y\\ 9z^2+1\geq 6z\)
Suy ra \(S\leq 6\)
Dấu = xảy ra khi \(x=1;y=\frac{1}{2}; z=\frac{1}{3}\)
Đúng 0
Bình luận (0)
Tìm Min/Max
A= y2-4y+9
B=x2-x+1
C=2x2-6x
A = y^2 - 4y + 9 = y^2 - 4y + 4 + 5
= ( y - 2 )^2 + 5 >= 5
Dấu ''='' xảy ra khi y = 2
Vậy GTNN A là 5 khi y = 2
B = x^2 - x + 1 = x^2 - x + 1/4 + 3/4 = ( x - 1/2 )^2 + 3/4 >= 3/4
Dấu ''='' xảy ra khi x = 1/2
Vậy GTNN B là 3/4 khi x = 1/2
C = 2x^2 - 6x = 2 ( x^2 - 3x + 9 / 4 - 9/4 )
= 2 ( x - 3/2 )^2 - 9/2 >= -9/2
Dấu ''='' xảy ra khi x = 3/2
Vậy GTNN C là -9/2 khi x = 3/2
Đúng 2
Bình luận (1)
a) Ta có: \(A=y^2-4y+9\)
\(=y^2-4y+4+5\)
\(=\left(y-2\right)^2+5\ge5\forall y\)
Dấu '=' xảy ra khi y=2
b) Ta có: \(B=x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
Đúng 0
Bình luận (0)
Cho
S
:
x
2
+
y
2
+
z
2
3
và
d
:
x
-
1
2
y
+
1
-
2...
Đọc tiếp
Cho S : x 2 + y 2 + z 2 = 3 và d : x - 1 2 = y + 1 - 2 = z - 1 . Biết d ∩ S = E , F . Tính EF.
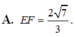
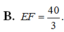
![]()
























