Tìm số dư cho phép chia
A = 1 + 5 + 52 + 53 + 54 +.....+ 52016 + 52017 cho 31
Những câu hỏi liên quan
Bài 1: Tìm x , y , z biết:
a) x5 = x3 (x Z)
b) (5x + 25)20 + (2y - 8)22 + (3z - 27)24 0 (x, y, z Z)
c) 2x + 168 = y2 (x, y N)
Bài 2 : Cho A = ; B = . So sánh A và B.
Bài 3: Cho A = 1 + 5 + 52 + 53 + … + 52016 + 52017 . tìm số dư trong phép chia A cho 31
Bài 4: Cho M = 9999932015 - 5555572017. Chứng minh rằng M chia hết cho 10.
Bài 1: Tìm x , y , z biết:
a) x5 = x3 (x Z)
b) (5x + 25)20 + (2y - 8)22 + (3z - 27)24 0 (x, y, z Z)
c) 2x + 168 = y2 (x, y N)
Bài 2 : Cho A = ; B = . So sánh A và B.
Bài 3: Cho A = 1 + 5 + 52 + 53 + … + 52016 + 52017 . tìm số dư trong phép chia A cho 31
Bài 4: Cho M = 9999932015 - 5555572017. Chứng minh rằng M chia hết cho 10.
16 tháng 10 2021 lúc 22:11
bài 6 :1) cho p và p + 8 đều là số nguyên tố (p3). hỏi p + 100 là số nguyên tố hay hợp số ?2) trog một phép chia,số bị chia bằng 63,số dư bằng 8. tìm số chia và thương 3) cho A 5 +52 + 53 +...+52016. Tìm x để 4A + 5 5x.4) chúng minh rằng tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.5) chứng tỏ rằng tổng A 405n + 2405 + m26) Cho S 1 + 3 + 32 + 33 + ...+ 398. Chứng minh S không phải là số chính phương.7) So sánh hai hiệu : 20182019 - 20182018 và 20182018 - 20182017.8) Khi ch...
Đọc tiếp
bài 6 :
1) cho p và p + 8 đều là số nguyên tố (p>3). hỏi p + 100 là số nguyên tố hay hợp số ?
2) trog một phép chia,số bị chia bằng 63,số dư bằng 8. tìm số chia và thương
3) cho A = 5 +52 + 53 +...+52016. Tìm x để 4A + 5 = 5x.
4) chúng minh rằng tích của 4 số tự nhiên liên tiếp cộng 1 luôn là số chính phương.
5) chứng tỏ rằng tổng A = 405n + 2405 + m2
6) Cho S = 1 + 3 + 32 + 33 + ...+ 398. Chứng minh S không phải là số chính phương.
7) So sánh hai hiệu : 20182019 - 20182018 và 20182018 - 20182017.
8) Khi chia một số cho 255 ta được số dư là 100. hỏi số đó chia hết cho 85 không? Vì sao? Nếu có dư thì số như là bao nhiêu?
9) Chứng minh rằng với mọi số tự nhiên n thì n2 + n +1 không chia hết cho 4.
mình chia 2 phần ạ. còn phần 2 mình sẽ viết. mong mn giúp mình ạ ^^ mình cần rất gấp vì mai mình đi học rồi. mn ko giúp mình là coi như mình toang luôn T-T
Xem thêm câu trả lời
a) Chứng minh: B = 31 + 32 + 33 + 34 + … + 32010 chia hết cho 4.
b) Chứng minh: C = 51 + 52 + 53 + 54 + … + 52010 chia hết cho 31.
c) Cho S=17+52+53+54+ ... +52010 . Tìm số dư khi chia S cho 31.
\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)
\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)
\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)
\(=4.\left(3+3^3+...+3^{2009}\right)\)
⇒ \(B\) ⋮ 4
Đúng 3
Bình luận (0)
b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)
Đúng 2
Bình luận (0)
14 tháng 3 2022 lúc 16:34
cho S = 5 + 52 + 53 + 54 + 55 + 56 +...+ 52016. chứng tỏ rằng S chia hết cho 65
mn giúp mk nhé!!
1)Tìm số dư của phép chia B cho 4
B=1+3+32+33+...+3100
2)Thu gọn C=5-52+53-54+...+52023-52024
Bài 1:
$B=1+3+3^2+3^3+...+3^{100}$
$=1+(3+3^2)+(3^3+3^4)+...+(3^{99}+3^{100})$
$=1+3(1+3)+3^3(1+3)+...+3^{99}(1+3)$
$=1+(1+3)(3+3^3+...+3^{99})=1+4(3+3^3+....+3^{99})$
$\Rightarrow B$ chia 4 dư 1.
Đúng 1
Bình luận (0)
Bài 2:
$C=5-5^2+5^3-5^4+...+5^{2023}-5^{2024}$
$5C=5^2-5^3+5^4-5^5+...+5^{2024}-5^{2025}$
$\Rightarrow C+5C=5-5^{2025}$
$6C=5-5^{2025}$
$C=\frac{5-5^{2025}}{6}$
Đúng 2
Bình luận (0)
21 tháng 11 2021 lúc 14:07
Bài 3. Tìm dư của phép chia tổng 51 + 52 + 53 + . . . + 52021 cho 31.
21 tháng 11 2021 lúc 14:15
Bài 3. Tìm dư của phép chia tổng 51 + 52 + 53 + . . . + 52021 cho 31.
\(=5+\left(5^2+5^3\right)+\left(5^4+5^5\right)+...+\left(5^{2020}+5^{2021}\right)\\ =5+5\left(5+5^2\right)+5^3\left(5+5^2\right)+...+5^{2019}\left(5+5^2\right)\\ =5+\left(5+5^2\right)\left(5+5^3+...+5^{2019}\right)\\ =5+31\left(5+5^3+...+5^{2019}\right)\)
Vậy BT chia 31 dư 5
Đúng 2
Bình luận (0)
bài 6:
a) Tìm cặp số x,y nguyên biết: (x - 3).(y+1)=5
b) Cho A = 21 + 5 + 52 + 53 + ... + 599.Tìm số dư của phép chia khi lấy A chia cho 6
Lời giải:
a. $(x-3)(y+1)=5=1.5=5.1=(-1)(-5)=(-5)(-1)$
Vì $x-3, y+1$ cũng là số nguyên nên ta có bảng sau:
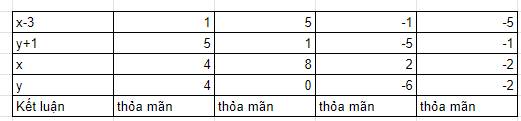
b.
$A=21+5+(5^2+5^3)+(5^4+5^5)+....+(5^{98}+5^{99})$
$=26+5^2(1+5)+5^4(1+5)+....+5^{98}(1+5)$
$=2+24+(1+5)(5^2+5^4+...+5^{98}$
$=2+24+6(5^2+5^4+....+5^{98})=2+6(4+5^2+5^4+...+5^{98})$
$\Rightarrow A$ chia $6$ dư $2$.
Đúng 2
Bình luận (0)
13 tháng 2 2022 lúc 20:40
a) Cho S = 5 + 52+ 53 + 54 + 55 + 56 +…+ 52012. Chứng tỏ S chia hết cho 65.
b) Tìm số tự nhiên nhỏ nhất sao cho khi chia cho 11 dư 6, chia cho 4 dư 1và chia cho 19 dư 11.
c) Chứng tỏ: A = 10n+ 18n - 1 chia hết cho 27 (với n là số tự nhiên)
a. S = 5 + 52 + 53 + 54 + 55 + 56 +...+ 52012.
S = (5 + 52 + 53 + 54) + 55(5 + 52 + 53 + 54)+....+ 52009(5 + 52 + 53 + 54)
Vì (5 + 52 + 53 + 54) = 780 chia hết cho 65
Vậy S chia hết cho 65
b. Gọi số cần tìm là a ta có: (a - 6) chia hết cho 11; (a - 1) chia hết cho 4; (a - 11) chia hết cho 19.
(a - 6 + 33) chia hết cho 11; (a - 1 + 28) chia hết cho 4; (a - 11 + 38) chia hết cho 19.
(a + 27) chia hết cho 11; (a + 27) chia hết cho 4; (a + 27) chia hết cho 19.
Do a là số tự nhiên nhỏ nhất nên a + 27 nhỏ nhất
Suy ra: a + 27 = BCNN (4;11; 19).
Từ đó tìm được: a = 809
A = 10n + 18n - 1 = 10n - 1 - 9n + 27n
Đúng 0
Bình luận (0)