\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)

\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)

\(b,\left(m-1\right)x^2-2mx+m-2=0\)

\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)

\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)

\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)

\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)

\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

1: mx+y=2m+2 và x+my=11

Khi m=-3 thì hệ sẽ là:

-3x+y=-6+2=-4 và x-3y=11

=>-3x+y=-4 và 3x-9y=33

=>-8y=29 và 3x-y=4

=>y=-29/8 và 3x=y+4=3/8

=>x=1/8 và y=-29/8

2: Để hệ có 1 nghiệm duy nhất thì \(\dfrac{m}{1}< >\dfrac{1}{m}\)

=>m^2<>1

=>m<>1 và m<>-1

Để hệ vô số nghiệm thì \(\dfrac{m}{1}=\dfrac{1}{m}=\dfrac{2m+2}{11}\)

=>(m=1 hoặc m=-1) và (11m=2m+2)

=>\(m\in\varnothing\)

Để hệ vô nghiệm thì m/1=1/m<>(2m+2)/11

=>m=1 hoặc m=-1

a: \(\Leftrightarrow\left(2m+1\right)^2-4\left(m^2-3\right)=0\)

\(\Leftrightarrow4m^2+4m+1-4m^2+12=0\)

=>4m=-13

hay m=-13/4

c: \(\Leftrightarrow\left(2m-2\right)^2-4m^2>=0\)

\(\Leftrightarrow4m^2-8m+4-4m^2>=0\)

=>-8m>=-4

hay m<=1/2

Pt vô nghiệm khi:

\(\Delta=\left(2m+1\right)^2-\left(5m^2+3m+16\right)< 0\)

\(\Leftrightarrow-m^2+m-15< 0\) (luôn đúng)

Vậy pt đã cho vô nghiệm với mọi m

\(\dfrac{x+1}{x+2}=\dfrac{x-1}{x-m}\)

\(\Leftrightarrow\left(x+1\right)\left(x-m\right)=\left(x+2\right)\left(x-1\right)\)

\(\Leftrightarrow x^2-xm+x-m=x^2+x-2\)

\(\Leftrightarrow-xm+2=0\)

Để pt vô nghiệm thì \(a\ne0\) nhưng trong TH này \(a=0\)

Vậy m không xác định

f(x) = (m + 1) x 2  - 2(3 - 2m)x + m + 1 ≥ 0 (1)

Với m = -1:

(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0

Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0

Suy ra, m = -1 (loại)

Với m ≠ -1:

f(x) = (m +1 ) x 2  - 2(3 - 2m)x + m + 1

Δ' = [-(3 - 2m) ] 2  - (m + 1)(m + 1) = (2m - 3 ) 2  - (m + 1 ) 2

= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)

Để bất phương trình (1) vô nghiệm thì:

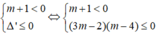
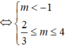
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm