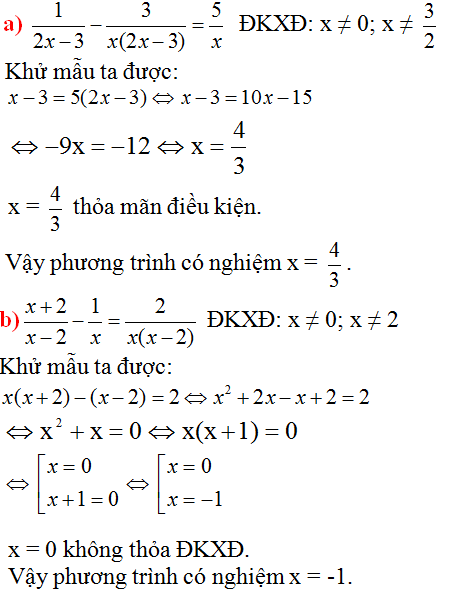(2,5-3x):=

(\(\frac{8}{5}\)+2x) . \(\frac{-17}{8}\)

2,45x = -4,9

x = -2

Tick và theo dõi mình nha

\(\dfrac{3}{x-5}-\dfrac{x+1}{x\left(x-5\right)}\left(dkxd:x\ne0,x\ne5\right)\\ =\dfrac{3x-x-1}{x\left(x-5\right)}=\dfrac{2x-1}{x^2-5x}\)

----------------------------------------

\(\dfrac{8\left(y+2\right)}{3x^2}.\dfrac{15x^5}{4\left(y+2\right)^2}\left(dkxd:x\ne0,y\ne-2\right)\\ =\dfrac{8}{4}.\dfrac{15x^2.x^3}{3x^2}=10x^3\)

------------------------------------------

\(\dfrac{8\left(y-1\right)}{3x^2-3}:\dfrac{4\left(y-1\right)^3}{x^2-2x+1}\left(dkxd:x\ne1,x\ne-1\right)\\ =\dfrac{8\left(y-1\right)}{3\left(x-1\right)\left(x+1\right)}.\dfrac{\left(x-1\right)^2}{4\left(y-1\right)^3}\\ =\dfrac{2\left(x-1\right)}{3\left(x+1\right)\left(y-1\right)^2}\)

ĐK: ` x \ne 2/7`

`(2x+3)((3x+8)/(2-7x)+1)=(x-5)((3x+8)/(2-7x)+1)`

`<=> ((3x+8)(2-7x)+1)(2x+3-x+5)=0`

`<=> ((3x+8)/(2-7x)+1)(x+8)=0`

 \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3x+8}{2-7x}=-1\\x+8=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-8\end{matrix}\right.\)

Vậy `S={5/2 ; -8}`.

\(\left(3-x\right)^3=-\dfrac{27}{64}\)

\(\left(3-x\right)^3=\left(\dfrac{-3}{4}\right)^3\)

\(=>3-x=\dfrac{-3}{4}\)

\(x=3-\dfrac{-3}{4}=\dfrac{12}{4}+\dfrac{3}{4}\)

\(x=\dfrac{15}{4}\)

________

\(\left(x-5\right)^3=\dfrac{1}{-27}\)

\(\left(x-5\right)^3=\left(\dfrac{-1}{3}\right)^3\)

\(=>x-5=\dfrac{-1}{3}\)

\(x=\dfrac{-1}{3}+5=\dfrac{-1}{3}+\dfrac{15}{3}\)

\(x=\dfrac{14}{3}\)

_____________

\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{27}{8}\)

\(\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{3}{2}\right)^3\)

\(=>x-\dfrac{1}{2}=\dfrac{3}{2}\)

\(x=\dfrac{3}{2}+\dfrac{1}{2}\)

\(x=2\)

________

\(\left(2x-1\right)^2=\dfrac{1}{4}\)            

\(\left(2x-1\right)^2=\left(\dfrac{1}{2}\right)^2\)           hoặc              \(\left(2x-1\right)^2=\left(\dfrac{-1}{2}\right)^2\)

\(=>2x-1=\dfrac{1}{2}\)                                       \(2x-1=\dfrac{-1}{2}\)

\(2x=\dfrac{1}{2}+1=\dfrac{1}{2}+\dfrac{2}{2}\)                               \(2x=\dfrac{-1}{2}+1=\dfrac{-1}{2}+\dfrac{2}{2}\)

\(2x=\dfrac{3}{2}\)                                                     \(2x=\dfrac{1}{2}\)

\(x=\dfrac{3}{2}:2=\dfrac{3}{2}.\dfrac{1}{2}\)                                     \(x=\dfrac{1}{2}:2=\dfrac{1}{2}.\dfrac{1}{2}\)

\(x=\dfrac{3}{4}\)                                                       \(x=\dfrac{1}{4}\)

____________

\(\left(2-3x\right)^2=\dfrac{9}{4}\)

\(\left(2-3x\right)^2=\left(\dfrac{3}{2}\right)^2\)                hoặc                  \(\left(2-3x\right)^2=\left(\dfrac{-3}{2}\right)^2\)

\(=>2-3x=\dfrac{3}{2}\)                                               \(2-3x=\dfrac{-3}{2}\)

\(3x=2-\dfrac{3}{2}=\dfrac{4}{2}-\dfrac{3}{2}\)                                      \(3x=2-\dfrac{-3}{2}=\dfrac{4}{2}+\dfrac{3}{2}\)

\(3x=\dfrac{1}{2}\)                                                            \(3x=\dfrac{7}{2}\)

\(x=\dfrac{1}{2}.\dfrac{1}{3}\)                                                          \(x=\dfrac{7}{2}.\dfrac{1}{3}\)

\(x=\dfrac{1}{6}\)                                                               \(x=\dfrac{7}{6}\)

______________

\(\left(1-\dfrac{2}{3}\right)^2=\dfrac{4}{9}\) -> Kiểm tra đề câu này

(3-x)^{3_{=(-\(\dfrac{3}{4}\))}3}

^{3-x=-\(\dfrac{3}{4}\)}

  ^{x=3-(-\(\dfrac{3}{4}\))}

  ^{x=\(\dfrac{15}{4}\)}

B

a) \(\dfrac{x+5}{3\left(x-1\right)}+1=\dfrac{3x+7}{5\left(x-1\right)}\) ( đk: \(x\ne1\))

\(\Leftrightarrow\dfrac{5\left(x+5\right)}{15\left(x-1\right)}+\dfrac{15\left(x-1\right)}{15\left(x-1\right)}=\dfrac{3\left(3x+7\right)}{15\left(x-1\right)}\)

\(\Rightarrow5\left(x+5\right)+15\left(x-1\right)=3\left(3x+7\right)\)

\(\Leftrightarrow5x+25+15x-15=9x+21\)

\(\Leftrightarrow5x+15x-9x=21-25+15\)

\(\Leftrightarrow11x=11\Leftrightarrow x=1\) (loại)

Vậy tập nghiệm: \(S=\varnothing\)

b) \(\dfrac{3x-1}{x-1}-\dfrac{2x+5}{x+3}-\dfrac{8}{x^2+2x-3}=1\)  (đk: \(x\ne1,x\ne-3\))

\(\Leftrightarrow\dfrac{\left(3x-1\right)\left(x+3\right)}{x^2+2x-3}-\dfrac{\left(2x+5\right)\left(x-1\right)}{x^2+2x-3}-\dfrac{8}{x^2+2x-3}=\dfrac{x^2+2x-3}{x^2+2x-3}\)

\(\Rightarrow\left(3x-1\right)\left(x+3\right)-\left(2x+5\right)\left(x-1\right)-8=x^2+2x-3\)

\(\Leftrightarrow3x^2+9x-x-3-2x^2+2x-5x+5-8=x^2+2x-3\)

\(\Leftrightarrow3x=3\Leftrightarrow x=1\) (loại)

Vậy tập nghiệm: \(S=\varnothing\)

1a.

ĐKXĐ: \(x\ne\left\{1;3\right\}\)

\(\Leftrightarrow\dfrac{6}{x-1}=\dfrac{4}{x-3}+\dfrac{4}{x-3}\)

\(\Leftrightarrow\dfrac{3}{x-1}=\dfrac{4}{x-3}\Leftrightarrow3\left(x-3\right)=4\left(x-1\right)\)

\(\Leftrightarrow3x-9=4x-4\Rightarrow x=-5\)

b.

ĐKXĐ: \(x\ne\left\{-1;2\right\}\)

\(\Leftrightarrow\dfrac{5}{x+1}=\dfrac{3}{2-x}+\dfrac{1}{2-x}\)

\(\Leftrightarrow\dfrac{5}{x+1}=\dfrac{4}{2-x}\Leftrightarrow5\left(2-x\right)=4\left(x+1\right)\)

\(\Leftrightarrow10-2x=4x+4\Leftrightarrow6x=6\Rightarrow x=1\)

1c.

ĐKXĐ: \(x\ne\left\{2;5\right\}\)

\(\Leftrightarrow\dfrac{3x\left(x-5\right)}{\left(x-2\right)\left(x-5\right)}-\dfrac{x\left(x-2\right)}{\left(x-2\right)\left(x-5\right)}=\dfrac{-3x}{\left(x-2\right)\left(x-5\right)}\)

\(\Leftrightarrow3x\left(x-5\right)-x\left(x-2\right)=-3x\)

\(\Leftrightarrow2x^2-10x=0\Leftrightarrow2x\left(x-5\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=5\left(loại\right)\end{matrix}\right.\)

2a.

\(\Leftrightarrow-4x^2-5x+6=x^2+4x+4\)

\(\Leftrightarrow5x^2+9x-2=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{5}\end{matrix}\right.\)

2b.

\(2x^2-6x+1=0\Rightarrow x=\dfrac{3\pm\sqrt{7}}{2}\)