Cho tam giasc ABC vuông tại A có C = 15 độ. Chứng minh : BC^2 = 4AB.AC
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A và góc C = 15 độ. Chứng minh rằng BC^2 = 4AB.AC.
11 tháng 10 2023 lúc 21:30
Đề bài: cho tam giác ABC vuông tại A có góc ABC = 15 độ. CMR BC^2=4AB.AC
=> \(\widehat{C}=180-90-15=70^o\)
Ta có:
\(sin15=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{sin15}=\dfrac{4AC}{\sqrt{6}-\sqrt{2}}\)
\(sin75=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sin75}=\dfrac{4AB}{\sqrt{6}+\sqrt{2}}\)
\(\Rightarrow BC^2=\dfrac{16.AB.AC}{\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{6}-\sqrt{2}\right)}=4.AB.AC\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có góc A=90 độ, góc ABC=15 độ, Chứng minh rằng: BC2=4AB.AC
cho tam giac ABC có góc A = 90 độ gọi d là đường thẳng đi qua C và vuông góc với BC . tia phân giác góc B cắt AC tại D và cắt đường thẳng d tại E . kẻ CH vuông với DE . chứng minh CH là phân giasc góc DCE
19 tháng 9 2020 lúc 13:43
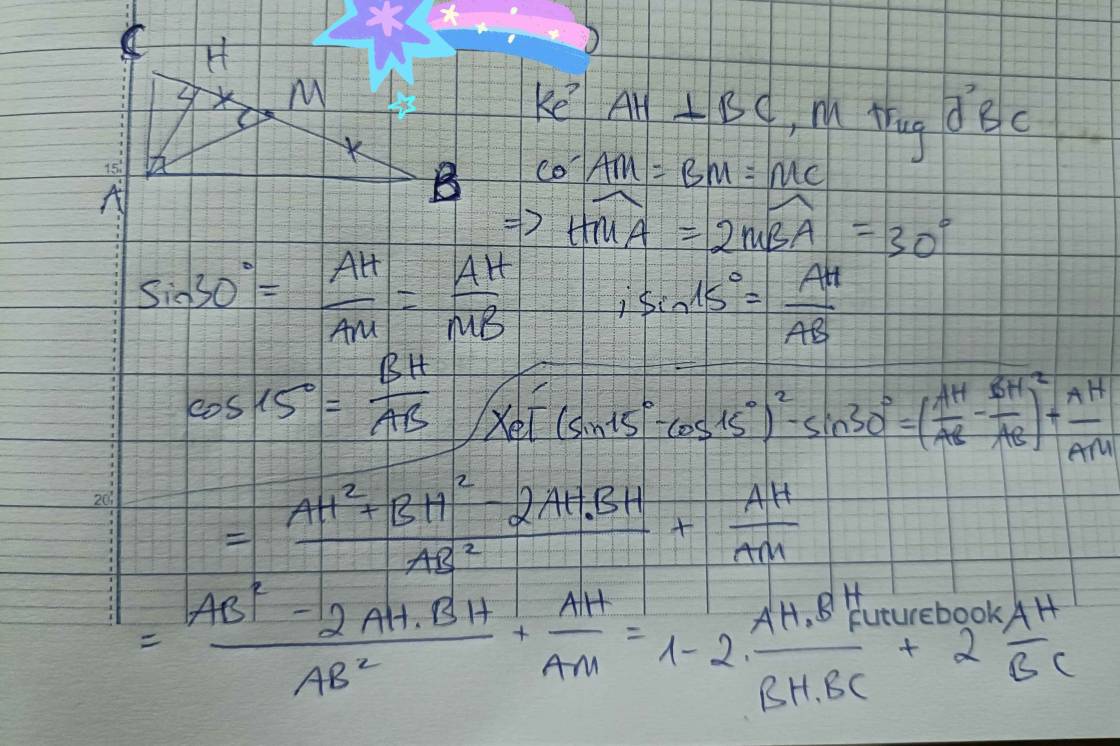
cho tam giác abc vuông tại a. trung tuyến am, đường cao ah. biết góc abc = 15 độ. cmr: bc^2 = 4ab.ac
Cho tam giasc ABC vuông tại A, gọi D là điểm đối xứng với A qua cạnh BC. Chứng minh tứ giác ABCD nội tiếp.
Giusp em với ạ!!!!!!!!!!
A đối xứng D qua BC
=>BA=BD và CA=CD
Xét ΔCAB và ΔCDB có
CA=CD
BA=BD
CB chung
=>ΔCAB=ΔCDB
=>góc CDB=90 độ
góc CAB+góc CDB=180 độ
=>CABD nội tiếp
Đúng 0
Bình luận (0)
Cho tam giasc ABC vuông tại A, gọi D là điểm đối xứng với A qua cạnh BC. Chứng minh tứ giác ABCD nội tiếp.
Giusp em với ạ!!!!!!!!!!
A đối xứng D qua BC
=>BA=BD và CA=CD
Xét ΔCAB và ΔCDB có
CA=CD
BA=BD
CB chung
=>ΔCAB=ΔCDB
=>góc CDB=góc CAB=90 độ
góc BAC+góc BDC=180 độ
=>BACD nội tiếp
Đúng 0
Bình luận (0)
-Cho tam giác ABC vuông tại A , có BC=2AB . Gọi H là trung điểm của BC , đường thẳng vuông góc với BC tại H cắt AC tại M.
a) Biết ABC = 60 độ , tính góc C ?
b) Chứng minh tam giác MAB = tam giác MHB.
c) Chứng minh tam giác MBC cân
d) Chứng minh BM là đường trung trực của AH
giúp với ạ cần hình gấp😭
28 tháng 7 2023 lúc 21:11
Cho tam giác ABC vuông tại A có góc C = 30 độ. Tia phân giác góc B cắt BC tại E. Từ E vẽ EH vuông góc với BC (H thuộc BC)
a, So sánh các cạnh của tam giác ABC
b, Chứng minh tam giác ABE = tam giác HBE
c, Chứng minh tam giác EAH cân
a: góc B=90-60=30 độ
Xét ΔABC có góc C<góc B<góc A
nên AB<AC<BC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
c: ΔBAE=ΔBHE
=>EA=EH
=>ΔEAH cân tại E
Đúng 2
Bình luận (1)