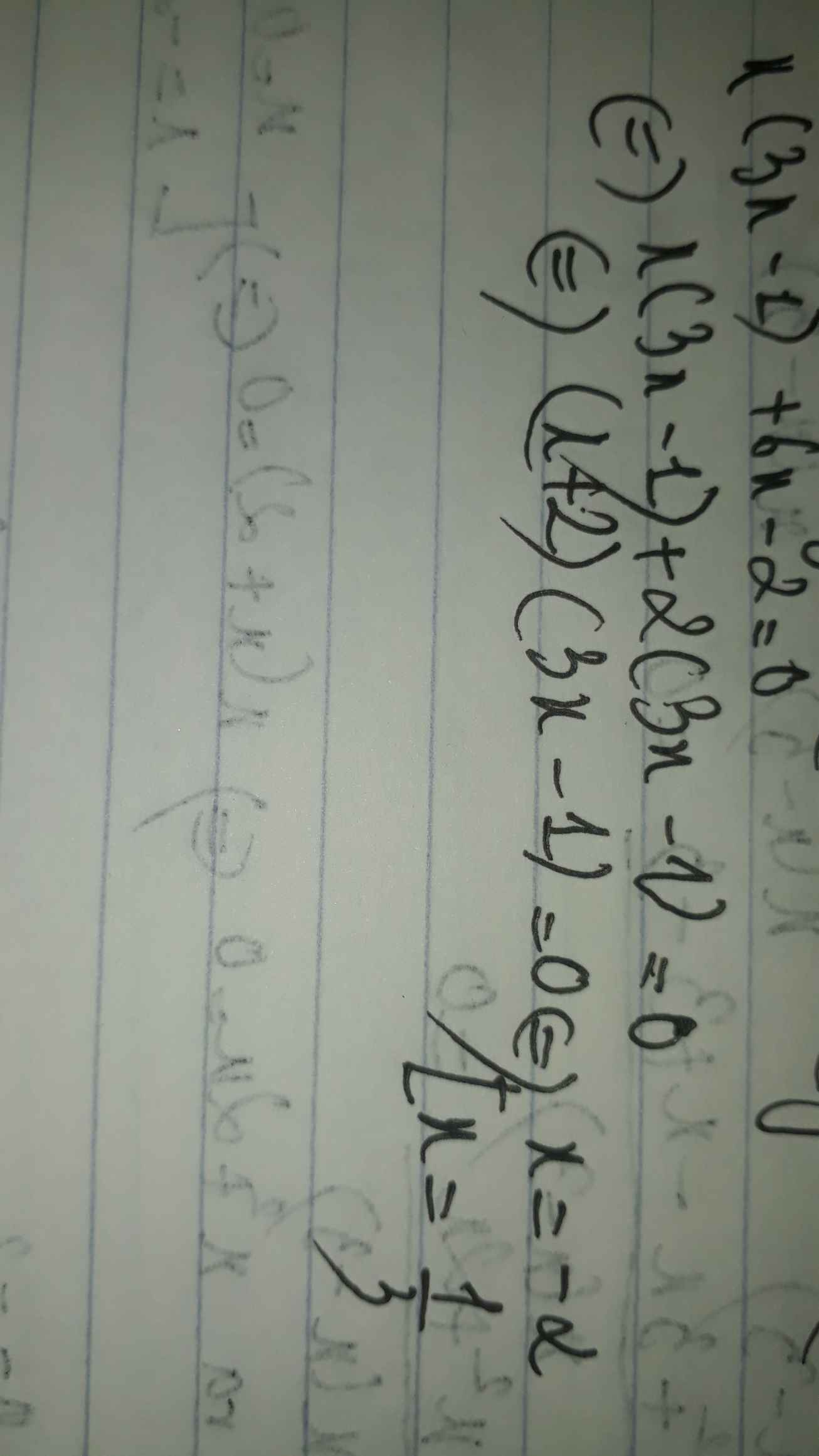\(\left|x^2-3x\right|+\left|\left(x+1\right)\left(x-3\right)\right|=0\)

=> \(\left|x\left(x-3\right)\right|+\left|\left(x+1\right)\left(x-3\right)\right|=0\)

Vì |x(x - 3)| \(\ge\)0 với mọi x

|(x + 1)(x - 3)| \(\ge\)0 với mọi x

=> Để \(\left|x\left(x-3\right)\right|+\left|\left(x+1\right)\left(x-3\right)\right|=0\)

=> \(\hept{\begin{cases}x\left(x-3\right)=0\\\left(x+1\right)\left(x-3\right)=0\end{cases}}\)

=> \(\hept{\begin{cases}x=0\text{ hoặc }x-3=0\\x+1=0\text{ hoặc }x-3=0\end{cases}}\)

=> \(\hept{\begin{cases}x=0\text{ hoặc }x=3\\x=-1\text{ hoặc }x=3\end{cases}}\)

Mà x ko thể cùng lúc nhận nhiều giá trị

=> x = 3 thỏa mãn đề bài 

a) \(\Rightarrow\dfrac{1}{3}x\left(x-2\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)

b) \(\Rightarrow\left(x+5\right)\left(x-1\right)=0\Rightarrow\left[{}\begin{matrix}x=-5\\x=1\end{matrix}\right.\)

c) \(\Rightarrow x\left(x^2-\dfrac{1}{9}\right)=0\Rightarrow x\left(x-\dfrac{1}{3}\right)\left(x+\dfrac{1}{3}\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)

e) \(\Rightarrow\left(x+2\right)\left(x+2-x+2\right)=0\Rightarrow\left(x+2\right).4=0\Rightarrow x=-2\)

f) \(\Rightarrow x\left(2x-3\right)+2\left(2x-3\right)=0\Rightarrow\left(2x-3\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-2\end{matrix}\right.\)

g) \(\Rightarrow2\left(3x-2\right)^2-\left(3x-2\right)\left(3x+2\right)=0\Rightarrow\left(3x-2\right)\left(3x-6\right)=0\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)

h) \(\Rightarrow x\left(x+1\right)\left(x+2\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=-1\\x=-2\end{matrix}\right.\)

i) \(\Rightarrow4x\left(x+1\right)+5\left(x+1\right)=0\Rightarrow\left(x+1\right)\left(4x+5\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{5}{4}\end{matrix}\right.\)

a) Ta có: \(\left(x-2\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=15\)

\(\Leftrightarrow x^3-6x^2+12x-8-x^3+27+6\left(x^2+2x+1\right)=15\)

\(\Leftrightarrow-6x^2+12x+19+6x^2+12x+6=15\)

\(\Leftrightarrow24x+25=15\)

\(\Leftrightarrow24x=-10\)

hay \(x=-\dfrac{5}{12}\)

b) Ta có: \(2x^3-50x=0\)

\(\Leftrightarrow2x\left(x-5\right)\left(x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)

c) Ta có: \(5x^2-4\left(x^2-2x+1\right)-5=0\)

\(\Leftrightarrow5x^2-4x^2+8x-4-5=0\)

\(\Leftrightarrow x^2+8x-9=0\)

\(\Leftrightarrow\left(x+9\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-9\\x=1\end{matrix}\right.\)

d) Ta có: \(x^3-x=0\)

\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

e) Ta có: \(27x^3-27x^2+9x-1=1\)

\(\Leftrightarrow\left(3x\right)^3-3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2-1^3=1\)

\(\Leftrightarrow\left(3x-1\right)^3=1\)

\(\Leftrightarrow3x-1=1\)

\(\Leftrightarrow3x=2\)

hay \(x=\dfrac{2}{3}\)

a)TH1: \(2x-3>0;3x+2>0\)

\(=>2x-3-3x-2=0\\ =>-x-5=0\\ =>-x=5=>x=-5\)

TH2: \(2x-3< 0;3x+2< 0\)

\(=>-2x+3+3x+2=0\\ =>x+5=0\\ =>x=-5\)

Cả 2 TH ra \(x=-5=>x=-5\)

b)TH1 \(\dfrac{1}{2}x>0\)

\(=>\dfrac{1}{2}x=3-2x\\ =>3-2x-\dfrac{1}{2}x=0\\ =>\dfrac{4}{2}x-\dfrac{1}{2}x=3\\ =>\dfrac{3}{2}x=3\\ =>x=2\)

TH2 \(\dfrac{1}{2}x< 0\)

\(=>-\dfrac{1}{2}x=3-2x\\ =>3-2x+\dfrac{1}{2}x=0\\ =>\dfrac{4}{2}x+\dfrac{1}{2}x=3\\ =>\dfrac{5}{2}x=3\\ =>x=\dfrac{6}{5}\)

\(=>x=2;\dfrac{6}{5}\)

:V lập 2 ý là làm đc á em 

xét 2 trường hợp là đc mà e :v

Rảnh rỗi thật sự .-.

\(\left(x-1\right)\left(3x+2\right)=0\)

\(\Rightarrow\)\(x-1=0\)hoặc \(3x+2=0\)

\(\Rightarrow\)\(x=1\)hoặc \(x=\frac{-2}{3}\)

bạn biến đổi kiểu j ra \(\left(x-1\right)\left(3x+2\right)=0\)

<=> (3x + 2)(x - 1) = 0

3x + 2 =0 (1) hoặc x - 1 =0 (2)

(1)<=> 3x+2=0

<=> 3x=-2

<=> x = -2/3

(2) <=> x-1=0

<=> x=1

Vậy.............

\(x\left(3x-1\right)+6x-2=0\)

\(\Leftrightarrow3x^2-x+6x-2=0\)

\(\Leftrightarrow3x^2+5x-2=0\)

\(\Leftrightarrow3x^2+6x-x-2=0\)

\(\Leftrightarrow3x\left(x+2\right)-\left(x+2\right)=0\)

\(\Leftrightarrow\left(3x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-1=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=-2\end{matrix}\right.\)

= 3x²-1+6x-2=0

= 3x²+6x-3=0

= 3x²+3x+3x-3=0

= (3x²+3x)+(3x-3)=0

= 3x(x+1)-3(x+1)=0

= (x+1)(3x-3)=0

= x+1=0 hoặc 3x-3=0

= x=1 hoặc 3x=3

                   x=1

vậy nghiệm của pt là S={1}

pt tương đương:

[(4x+1)(3x+2)][(12x-1)(x+1)]=700

<=>(12x²+11x+2)(12x²+11x-1)=700

Đặt t=12x²+11x pt trở thành

(t+2)(t-1)=700

<=>t²+t-702=0

<=>t=26 hoặc t=-27

với t=26 =>x=13/12 hoặc x=-2

với t=-27 không có x

a/ \(x=\dfrac{-5}{12}\)

b/ \(x\approx-1,9526\)

c/ \(x=\dfrac{21-i\sqrt{199}}{10}\)

d/ \(x=\dfrac{-20}{13}\)

a) (x-2)³+6(x+1)²-x³+12=0

⇒ x³-6x²+12x-8+6(x²+2x+1)-x³+12=0

⇒ x³-6x²+12x-8+6x²+12x+6-x³+12=0

⇒ 24x+10=0

⇒ 24x=-10

⇒ x=-5/12

a.

PT \(\Leftrightarrow x^3-6x^2+12x-8+6(x^2+2x+1)-x^3+12=0\)

\(\Leftrightarrow x^3-6x^2+12x-8+6x^2+12x+6-x^3+12=0\)

\(\Leftrightarrow 24x+10=0\Leftrightarrow x=\frac{-5}{12}\)

b. Bạn xem lại đề, nghiệm khá xấu không phù hợp với mức độ tổng thể của bài.

c.

PT $\Leftrightarrow (4x^2+12x+9)+(x^2-1)=5(x^2+4x+4)+(x^2-4x-5)+9(x^2+6x+9)$
$\Leftrightarrow 10x^2+42x+64=0$

$\Leftrightarrow x^2+(3x+7)^2=-15< 0$ (vô lý) 

Do đó pt vô nghiệm.

d.

PT $\Leftrightarrow (1-6x+9x^2)-(9x^2-17x-2)=(9x^2-16)-9(x^2+6x+9)$

$\Leftrightarrow 11x+3=-54x-97$

$\Leftrightarrow 65x=-100$

$\Leftrightarrow x=\frac{-20}{13}$