Cho hàm số y=-2x^3+3mx^2-1. Tìm m để y'>0 trên khoảng (x1;x2) với x2-x1=1

Những câu hỏi liên quan
Tìm m để hàm số
y
-
x
3
+
3
x
2
+
3
m
x
+
m
-
1
nghịch biến trên khoảng
(
0...
Đọc tiếp
Tìm m để hàm số y = - x 3 + 3 x 2 + 3 m x + m - 1 nghịch biến trên khoảng ( 0 ; + ∞ )
A. m > - 1
B. m ≤ - 1
C. m ≤ 1
D. m < 1
Cho hàm số
y
-
x
3
+
3
x
2
+
3
m
x
-
1
, tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞) A. m 1 B. m ≥ 1 C. m ≤ -1 D. m ≥ -1
Đọc tiếp
Cho hàm số y = - x 3 + 3 x 2 + 3 m x - 1 , tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
A. m < 1
B. m ≥ 1
C. m ≤ -1
D. m ≥ -1
Ta có y ' = - 3 x 2 + 6 x + 3 m . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình - 3 x 2 + 6 x + 3 m . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, - 3 x 2 + 6 x + 3 m < 0 nên hàm số nghịch biến trên R .
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
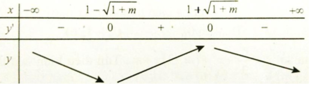
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số.
Ta có y ' = - 3 x 2 + 6 x + 3 m ≤ 0 , ∀x > 0 <=> 3 m ≤ 3 x 2 - 6 x , ∀x > 0
Từ đó suy ra 3 m ≤ m i n ( 3 x 2 - 6 x ) với x > 0
Mà 3 x 2 - 6 x = 3 ( x 2 - 2 x + 1 ) - 3 = 3 ( x - 1 ) 2 - 3 ≥ - 3 ∀ x
Suy ra: m i n ( 3 x 2 – 6 x ) = - 3 khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hàm số \(y=-x^3+3x^2+3mx-1\left(1\right)\), với m là tham số thực. Tìm m để hàm số (1) nghịch biến trên khoảng (\(0;+\infty\))
Ta có \(y'=-3x^2+6x+3m\) \(\Rightarrow\) hàm số nghịch biến trên khoảng \(\left(0;+\infty\right)\)\(\Leftrightarrow y'\le0\)
với mọi \(x\in\left(0;+\infty\right)\) (*)
Vì \(y'\left(x\right)\) liên tục tại x=0 nên (*)
\(\Leftrightarrow y'\le0\)với mọi \(x\in\)[0;\(+\infty\))
\(\Leftrightarrow-3x^2+6x+3m\le0\) với mọi \(x\in\)[0;\(+\infty\))
\(\Leftrightarrow m\le x^2-2x\), với mọi \(x\in\)[0;\(+\infty\))\(\Leftrightarrow m\le g\left(x\right);\)với mọi \(x\in\)[0;\(+\infty\)) (Trong đó \(g\left(x\right)=x^2-2x\)
\(\Leftrightarrow m\le Min_{\left(0;+\infty\right)}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=x^2-2x\) trên với mọi \(x\in\)[0;\(+\infty\))\(\Rightarrow g'\left(x\right)=2x-2\Rightarrow g'\left(x\right)=0\Leftrightarrow x=1\)
\(\lim\limits_{x\rightarrow+\infty}g\left(x\right)=+\infty;g\left(0\right)=0;g\left(1\right)=-1\)\(\Rightarrow Min_{\left(0;+\infty\right)}g\left(x\right)=-1\) tại x=1
Vậy \(m\le-1\) thì hàm số nghịch biến trên khoảng \(\left(0;+\infty\right)\)
Đúng 0
Bình luận (0)
1,Tìm tất cả các giá trị của m để hàm số y2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x2.
2, Tìm tất cả các giá trị của m để hàm số y x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x2.
3, Tìm tất cả các giá trị của m để hàm số yx^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu .
4, Tìm m để hso yx^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu.
Mọi người giúp em với ạ . Em cảm ơn ạ !
Đọc tiếp
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Cho hàm số \(y=-\frac{m-1}{3}x^3+\left(m+2\right)x^2+3mx+5\), với m là tham số thực. Tìm m để hàm số đồng biến trên khoảng \(\left(-\infty;-2\right)\)
Ta có \(y'=-\left(m-1\right)x^2+2\left(m+2\right)+3m\) \(\Rightarrow\) Hàm đồng biến trên khoảng \(\left(-\infty;-2\right)\Leftrightarrow y'\ge0,x\in\left(-\infty;-2\right)\)(*)
Vì y'(x) liên tục tại x = -2 nên (*) \(\Leftrightarrow y'\ge0;\)
và mọi x thuộc (-\(-\infty;2\) ] (*)
\(\Leftrightarrow-\left(m-1\right)x^2+2\left(m+2\right)x+3m\ge0\), mọi x thuộc (-\(-\infty;2\) ]
\(\Leftrightarrow m\left(-x^2+2x+3\right)\ge-x^2-4x\), mọi x thuộc (-\(-\infty;2\) ]\(\Leftrightarrow m\le g\left(x\right)\), mọi x thuộc (-\(-\infty;2\) ] (Trong đó \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\))
\(\Leftrightarrow m\le Min_{\left(-\infty;-2\right)}g\left(x\right)\)
Xét hàm số \(g\left(x\right)=\frac{-x^2-4x}{-x^2+2x+3}\) trên đoạn (-\(-\infty;2\) ]
\(\Rightarrow g'\left(x\right)=\frac{-6\left(x^2+x+2\right)}{\left(-x^2+2x+3\right)^2}=\frac{-6\left(x+\frac{1}{2}\right)^2+\frac{7}{4}}{\left(-x^2+2x+3\right)^2}<0\),mọi x thuộc (-\(-\infty;2\) ]
\(\Rightarrow g\left(x\right)\) là hàm số nghịch biến trên (-\(-\infty;2\) ]
\(\Rightarrow Min_{\left(-\infty;-2\right)}g\left(x\right)=g\left(-2\right)=-\frac{4}{5}\)
Vậy \(m\le-\frac{4}{5}\) thì hàm số đồng biến trên khoảng \(\left(-\infty;-2\right)\)
Đúng 0
Bình luận (0)
tìm m để hàm số y= 1/3mx^3 - (m-1)x^2 +3(m-2)x+1/3 đồng biến trên [2;+vc)
\(y'=mx^2-2\left(m-1\right)x+3\left(m-2\right)\)
\(y'\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow mx^2-2\left(m-1\right)x+3\left(m-2\right)\ge0\) ; \(\forall x\ge2\)
\(\Leftrightarrow mx^2-2mx+3m\ge6-x\)
\(\Leftrightarrow m\left(x^2-2x+3\right)\ge6-x\)
\(\Leftrightarrow m\ge\dfrac{6-x}{x^2-2x+3}\)
\(\Rightarrow m\ge\max\limits_{x\ge2}\dfrac{6-x}{x^2-2x+3}=\dfrac{4}{3}\)
Vậy \(m\ge\dfrac{4}{3}\)
Đúng 2
Bình luận (2)
cho hàm số y = x^3 + 3mx^2 +3(1-m^2)x+m^3-m
tìm m để đồ thị hàm số có 2 điểm cực tiểu nằm về cungd một phía của đường y=1(không nằm trên đườngthẳng)
Cho hàm số y=\(\dfrac{2x+m}{\sqrt{x-2m-1}-3}\)
Tìm m để hàm số xác định trên khoảng (0;+vô cùng). trình bày cách làm rõ nhá
100% group làm sai
cho hàm số y=1/2x^2 có đồ thị (P). Tìm m để đg thẳng d: y=3mx-2 cắt (P) tại 2 điểm phân biệt
Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2-3mx+2=0\)
\(\text{Δ}=\left(-3m\right)^2-4\cdot\dfrac{1}{2}\cdot2=9m^2-4\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow\left[{}\begin{matrix}m>\dfrac{2}{3}\\m< -\dfrac{2}{3}\end{matrix}\right.\)
Đúng 0
Bình luận (0)



















