1) \(\dfrac{1}{27}+a^3=\left(\dfrac{1}{3}+a\right)\left(\dfrac{1}{9}-\dfrac{a}{3}+a^2\right)\)

2) \(=\left(2x+3y\right)\left(4x^2-6xy+9y^2\right)\)

3) \(=\left(\dfrac{1}{2}x+2y\right)\left(\dfrac{1}{4}x-xy+4y^2\right)\)

4) \(=\left(x^2+1\right)\left(x^4-x^2+1\right)\)

5) \(=\left(x^3+1\right)\left(x^6-x^3+1\right)\)

6) \(=\left(x-4\right)\left(x^2+4x+16\right)\)

7) \(=\left(x-5\right)\left(x^2+5x+25\right)\)

8) \(=\left(2x^2-3y\right)\left(4x^4+6x^2y+9y^2\right)\)

9) \(=\left(\dfrac{1}{4}x^2-5y\right)\left(\dfrac{1}{16}x^4+\dfrac{5}{4}x^2y+25y^2\right)\)

10) \(=\left(\dfrac{1}{2}x-2\right)\left(\dfrac{1}{4}x^2+x+4\right)\)

11) \(=\left(x+2\right)^3\)

12) \(=\left(x+3\right)^3\)

\(\left(3-x\right)^3=-\dfrac{27}{64}\)

\(\left(3-x\right)^3=\left(\dfrac{-3}{4}\right)^3\)

\(=>3-x=\dfrac{-3}{4}\)

\(x=3-\dfrac{-3}{4}=\dfrac{12}{4}+\dfrac{3}{4}\)

\(x=\dfrac{15}{4}\)

________

\(\left(x-5\right)^3=\dfrac{1}{-27}\)

\(\left(x-5\right)^3=\left(\dfrac{-1}{3}\right)^3\)

\(=>x-5=\dfrac{-1}{3}\)

\(x=\dfrac{-1}{3}+5=\dfrac{-1}{3}+\dfrac{15}{3}\)

\(x=\dfrac{14}{3}\)

_____________

\(\left(x-\dfrac{1}{2}\right)^3=\dfrac{27}{8}\)

\(\left(x-\dfrac{1}{2}\right)^3=\left(\dfrac{3}{2}\right)^3\)

\(=>x-\dfrac{1}{2}=\dfrac{3}{2}\)

\(x=\dfrac{3}{2}+\dfrac{1}{2}\)

\(x=2\)

________

\(\left(2x-1\right)^2=\dfrac{1}{4}\)            

\(\left(2x-1\right)^2=\left(\dfrac{1}{2}\right)^2\)           hoặc              \(\left(2x-1\right)^2=\left(\dfrac{-1}{2}\right)^2\)

\(=>2x-1=\dfrac{1}{2}\)                                       \(2x-1=\dfrac{-1}{2}\)

\(2x=\dfrac{1}{2}+1=\dfrac{1}{2}+\dfrac{2}{2}\)                               \(2x=\dfrac{-1}{2}+1=\dfrac{-1}{2}+\dfrac{2}{2}\)

\(2x=\dfrac{3}{2}\)                                                     \(2x=\dfrac{1}{2}\)

\(x=\dfrac{3}{2}:2=\dfrac{3}{2}.\dfrac{1}{2}\)                                     \(x=\dfrac{1}{2}:2=\dfrac{1}{2}.\dfrac{1}{2}\)

\(x=\dfrac{3}{4}\)                                                       \(x=\dfrac{1}{4}\)

____________

\(\left(2-3x\right)^2=\dfrac{9}{4}\)

\(\left(2-3x\right)^2=\left(\dfrac{3}{2}\right)^2\)                hoặc                  \(\left(2-3x\right)^2=\left(\dfrac{-3}{2}\right)^2\)

\(=>2-3x=\dfrac{3}{2}\)                                               \(2-3x=\dfrac{-3}{2}\)

\(3x=2-\dfrac{3}{2}=\dfrac{4}{2}-\dfrac{3}{2}\)                                      \(3x=2-\dfrac{-3}{2}=\dfrac{4}{2}+\dfrac{3}{2}\)

\(3x=\dfrac{1}{2}\)                                                            \(3x=\dfrac{7}{2}\)

\(x=\dfrac{1}{2}.\dfrac{1}{3}\)                                                          \(x=\dfrac{7}{2}.\dfrac{1}{3}\)

\(x=\dfrac{1}{6}\)                                                               \(x=\dfrac{7}{6}\)

______________

\(\left(1-\dfrac{2}{3}\right)^2=\dfrac{4}{9}\) -> Kiểm tra đề câu này

(3-x)^{3_{=(-\(\dfrac{3}{4}\))}3}

^{3-x=-\(\dfrac{3}{4}\)}

  ^{x=3-(-\(\dfrac{3}{4}\))}

  ^{x=\(\dfrac{15}{4}\)}

\(\dfrac{45^{10}\cdot5^{20}}{75^{15}}=\dfrac{\left(3^2\cdot5\right)^{10}\cdot5^{20}}{\left(3\cdot5^2\right)^{15}}=\dfrac{3^{20}\cdot5^{10}\cdot5^{20}}{3^{15}\cdot5^{30}}=3^5=243\\ \dfrac{6^6+6^3+3^3+3^6}{-73}=\dfrac{46656+216+27+729}{-73}=-\dfrac{47628}{73}\\ \dfrac{27^7+3^{15}}{9^9-27}=\dfrac{\left(3^3\right)^7+3^{15}}{\left(3^2\right)^9-3^3}=\dfrac{3^{21}+3^{15}}{3^{18}-3^3}=\dfrac{3^{15}\left(3^6+1\right)}{3^3\left(3^{15}-1\right)}=\dfrac{3^5\cdot730}{3^{15}-1}\\ \dfrac{8^{20}+4^{20}}{4^{25}+64^5}=\dfrac{\left(2^3\right)^{20}+\left(2^2\right)^{20}}{\left(2^2\right)^{25}+\left(2^6\right)^5}=\dfrac{2^{60}+2^{40}}{2^{50}+2^{30}}=\dfrac{2^{40}\left(2^{20}+1\right)}{2^{30}\left(2^{20}+1\right)}=2^{10}=1024\)

a) \(\dfrac{2}{5}-\dfrac{3}{15}\)

\(=\dfrac{2}{5}-\dfrac{3:3}{15:3}\)

\(=\dfrac{2}{5}-\dfrac{1}{5}\)

\(=\dfrac{1}{5}\)

b) \(\dfrac{9}{27}-\dfrac{2}{9}\)

\(=\dfrac{9:3}{27:3}-\dfrac{2}{9}\)

\(=\dfrac{3}{9}-\dfrac{2}{9}\)

\(=\dfrac{1}{9}\)

c) \(\dfrac{18}{24}-\dfrac{4}{8}\)

\(=\dfrac{18:6}{24:6}-\dfrac{4:2}{8:2}\)

\(=\dfrac{3}{4}-\dfrac{2}{4}\)

\(=\dfrac{1}{4}\)

d) \(\dfrac{6}{16}-\dfrac{10}{64}\)

\(=\dfrac{6\times2}{16\times2}-\dfrac{10:2}{64:2}\)

\(=\dfrac{12}{32}-\dfrac{5}{32}\)

\(=\dfrac{7}{32}\)

Đề bài là:Tính các giá trị biểu thức sau ạ

a: \(=\left(9-\dfrac{13}{18}\right):\dfrac{325}{27}-\dfrac{17}{8}:\dfrac{51}{40}\)

\(=\dfrac{149}{18}\cdot\dfrac{27}{325}-\dfrac{17}{8}\cdot\dfrac{40}{51}\)

\(=\dfrac{447}{650}-\dfrac{5}{3}=-\dfrac{1909}{1950}\)

b: \(=\dfrac{48}{64}+\left(\dfrac{4}{5}-2-\dfrac{4}{15}\right):\dfrac{11}{3}\)

\(=\dfrac{3}{4}+\dfrac{-22}{15}\cdot\dfrac{3}{11}=\dfrac{3}{4}-\dfrac{2}{5}=\dfrac{15-8}{20}=\dfrac{7}{20}\)

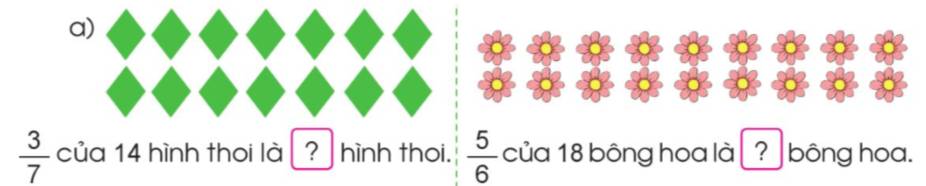
a) \(\dfrac{3}{7}\) của 14 hình thoi là \(6\) hinh thoi 

\(\dfrac{5}{6}\) của 18 bông hoa là \(15\) bông hoa 

b) \(\dfrac{1}{3}\) của 18 là: \(6\)

\(\dfrac{2}{7}\) của 42 là: \(12\)

\(\dfrac{3}{5}\) của 80 là: \(48\) 

\(\dfrac{1}{8}\) của 64 là: \(8\)

\(\dfrac{4}{9}\) của 27 là: \(12\) 

\(\dfrac{5}{8}\) của 96 là: \(60\)

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=\dfrac{-3x-4y+5z+3-12-25}{-3\cdot2-4\cdot4+5\cdot6}=\dfrac{16}{8}=2\)

Do đó: x=5; y=5; z=17

\(a,\dfrac{x^3}{8}=\dfrac{y^3}{27}=\dfrac{z^3}{64}\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\Rightarrow\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{16}\)

Áp dụng t/c dtsbn:

\(\dfrac{x^2}{4}=\dfrac{y^2}{9}=\dfrac{z^2}{16}=\dfrac{x^2+2y^2-3z^2}{4+18-48}=\dfrac{-650}{-26}=25\\ \Rightarrow\left\{{}\begin{matrix}x^2=100\\y^2=225\\z^2=400\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm10\\y=\pm15\\z=\pm20\end{matrix}\right.\)

Vậy \(\left(x;y;z\right)\) có giá trị là hoán vị của \(\left(\pm10;\pm15;\pm20\right)\)

\(\dfrac{\left(2^8-2^6\right)^3}{64^4}=\dfrac{27}{64}\)

\(\dfrac{192^3}{64^4}=\dfrac{27}{64}\)

\(\dfrac{\left(3\times64\right)^3}{64^3\times64}=\dfrac{27}{64}\)

\(\dfrac{3^3\times64^3}{64\times64^3}=\dfrac{27}{64}\)

\(\dfrac{3^3}{64}=\dfrac{27}{64}\)

\(\dfrac{27}{64}=\dfrac{27}{64}\)

ai giúp mìn vứi ❤