Cho hàm số f(x) = 2x\(^2\)-x. Giải phương trình f '(x)\(\sqrt{x^2+1}\) = 2x\(^2\)+2x+1

Những câu hỏi liên quan
Cho hàm số f(x) có đạo hàm là
f
(
x
)
x
4
(
2
x
+
1
)
2
(
x
-
1
)
. Số điểm cực trị của hàm số f(x) là A. 1. B. 2. C. 0. D. 3.
Đọc tiếp
Cho hàm số f(x) có đạo hàm là f ' ( x ) = x 4 ( 2 x + 1 ) 2 ( x - 1 ) . Số điểm cực trị của hàm số f(x) là
A. 1.
B. 2.
C. 0.
D. 3.
Đáp án A
Ta có
![]()
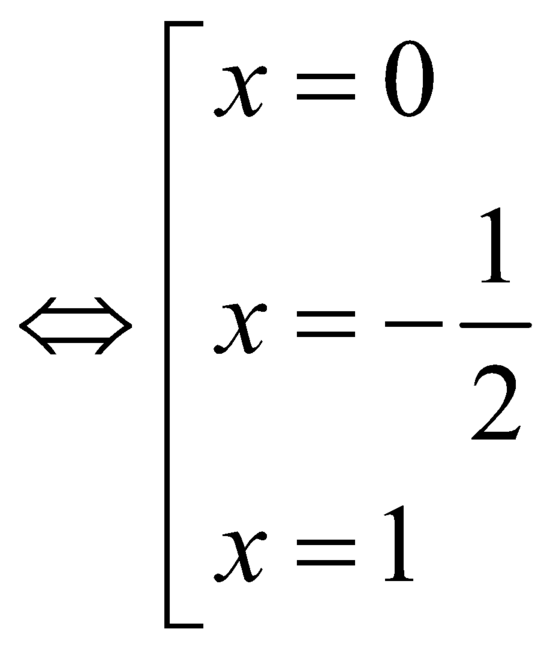 .
.
Bảng xét dấu:
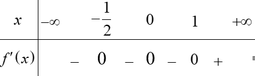
Suy ra hàm số có một điểm cực trị.
Đúng 0
Bình luận (0)
Bài 19: Cho f(x) 2x + 3. Tính f(3); f(); f(– 2).Bài 20: Cho g(x) 15/x. Tính f(3); f(5); f(– 2).Bài 21: Vẽ đồ thị các hàm số: y 1/2x ; y – 2x; y 3/2xBài 22: Vẽ đồ thị hàm số: y 3x, kiểm tra điểm A(– 2; 6) có thuộc đồ thị hàm số trên không? Vì sao? làm giúp em vs mn mai e thi r
Đọc tiếp
Bài 19: Cho f(x) = 2x + 3. Tính f(3); f(![]() ); f(– 2).
); f(– 2).
Bài 20: Cho g(x) = 15/x. Tính f(3); f(5); f(– 2).
Bài 21: Vẽ đồ thị các hàm số: y = 1/2x ; y = – 2x; y =3/2x
Bài 22: Vẽ đồ thị hàm số: y = 3x, kiểm tra điểm A(– 2; 6) có thuộc đồ thị hàm số trên không? Vì sao?
làm giúp em vs mn mai e thi r
Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x
Đúng 0
Bình luận (0)
Bài 19:
f(3)=2x3+3=9
f(-2)=-4+3=-1
Bài 20:
f(3)=15/3=5
f(5)=15/5=3
f(-2)=15/-2=-15/2
Bài 22:
Thay x=-2 vào y=3x, ta được:
y=3x(-2)=-6
Vậy: A(-2;6) thuộc đồ thị hàm số y=3x
Đúng 0
Bình luận (0)
Bài 1: Cho hàm số y = f(x) = 5 - 2x
a) Tính f(-2); f(-1)
b) Tính các giá trị của x ứng với các giá trị của y lần lượt là 5; 3; -1
Bài 2: Tìm tập xác định của các hàm số sau:
a) y = x3 - 2x2 + x -1
b) y = \(\sqrt{2x-1}\)
c) y = \(\frac{x-1}{\left(x+1\right)\left(x-3\right)}\)
Cho hàm số f(x)=(x\(^2\)+2*x)*\(\sqrt{x-1}\) .Giải bất phương trình f ' (x) >=0
M.n giải hộ mình câu này với ạ.Cảm ơn mn nhiều
\(x>1\)
\(f'\left(x\right)=\left(2x+2\right)\sqrt{x-1}+\frac{x^2+2x}{2\sqrt{x-1}}=\frac{5x^2+2x-4}{2\sqrt{x-1}}\)
\(f'\left(x\right)\ge0\Leftrightarrow\frac{5x^2+2x-4}{\sqrt{x-1}}\ge0\Leftrightarrow5x^2+2x-4\ge0\)
\(\Rightarrow x>1\)
Đúng 0
Bình luận (2)
Cho hàm số y=f(x)=1/2x-1/2
a Tính f(-3);f=(3/4)
b Tìm x biết f(x)=1/2
Answer:
a)
\(y=f\left(x\right)=\frac{1}{2}x-\frac{1}{2}\)
Tính \(f\left(-3\right)\): \(\frac{1}{2}.\left(-3\right)-\frac{1}{2}=\frac{-3}{2}-\frac{1}{2}=-2\)
Tính \(f\left(\frac{3}{4}\right)\) : \(\frac{1}{2}.\frac{3}{4}-\frac{1}{2}=\frac{3}{8}-\frac{1}{2}=\frac{-1}{8}\)
b)
\(\frac{1}{2}x-\frac{1}{2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{2}x=\frac{1}{2}+\frac{1}{2}\)
\(\Leftrightarrow\frac{1}{2}x=1\)
\(\Leftrightarrow x=1:\frac{1}{2}\)
\(\Leftrightarrow x=2\)
giải bất phương trình \(\sqrt{x+1}\le\frac{x^2-x-2\sqrt[3]{2x+1}}{\sqrt[3]{2x+1}-3}\)
Giải phương trình:
\(a)\sqrt{x^2+x+6}-\sqrt{x+3}=\sqrt{2x^2-5x+2}-\sqrt{2x-1}\)
\(b)\sqrt{x+1}+\sqrt{2x+3}=x^2-4\)
Giải phương trình:
\(a)\sqrt{x^2+x+6}-\sqrt{x+3}=\sqrt{2x^2-5x+2}-\sqrt{2x-1}\)
b)\(\sqrt{x+1}+\sqrt{2x+3}=x^2-4\).
Giải phương trình: \(-2\left(\sqrt{1+x}+\sqrt{1-x}\right)+7=\sqrt{\left(5-2x\right)\left(5+2x\right)}-2\sqrt{1-x^2}\)
\(-2\left(\sqrt{1+x}+\sqrt{1-x}\right)+7=\sqrt{\left(5-2x\right)\left(5+2x\right)}-2\sqrt{1-x^2}\)
ĐKCĐ: \(-1\le x\le1\)
\(\Leftrightarrow2\left(\sqrt{\left(1-x\right)}-1\right)\left(\sqrt{1+x}-1\right)+5-\sqrt{\left(5-2x\right)\left(5+2x\right)}=0\)
\(\Leftrightarrow2x^2\left[\frac{2}{5+\sqrt{\left(5-2x\right)\left(5+2x\right)}}-\frac{1}{\left(\sqrt{1-x}+1\right)\left(\sqrt{1+x}+1\right)}\right]\)
Đặt: \(A=\frac{2}{5+\sqrt{\left(5-2x\right)\left(5+2x\right)}}-\frac{1}{\left(\sqrt{1-x}+1\right)\left(\sqrt{1+x}+1\right)}\)
Có: \(A\le\frac{2}{5+\sqrt{\left(5-2\right)\left(5-2\right)}}-\frac{1}{\sqrt{1-x^2}+1+\sqrt{1-x}+\sqrt{1+x}}< \frac{2}{5+3}-\frac{1}{1+1+2}=0\)
\(\Rightarrow x=0\) là nghiệm của pt
![]()
![]()
Đúng 0
Bình luận (3)
Xem thêm câu trả lời

















