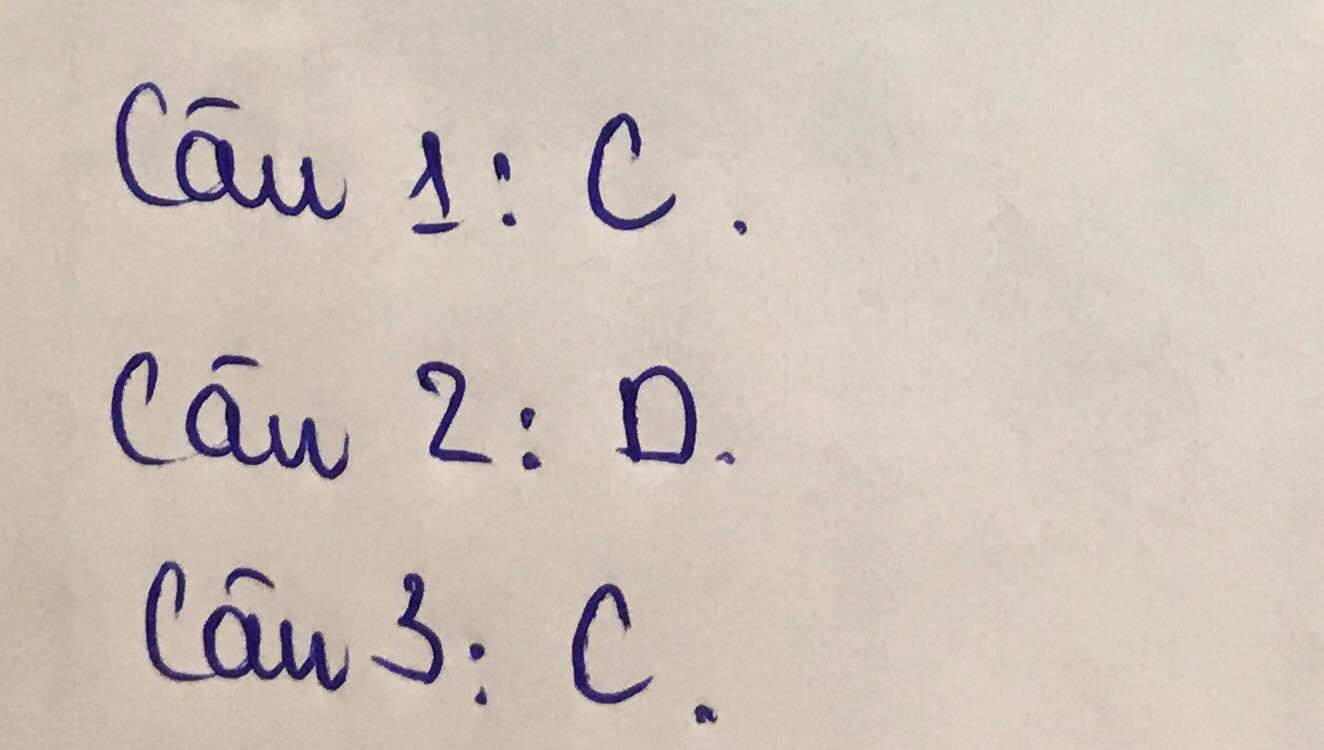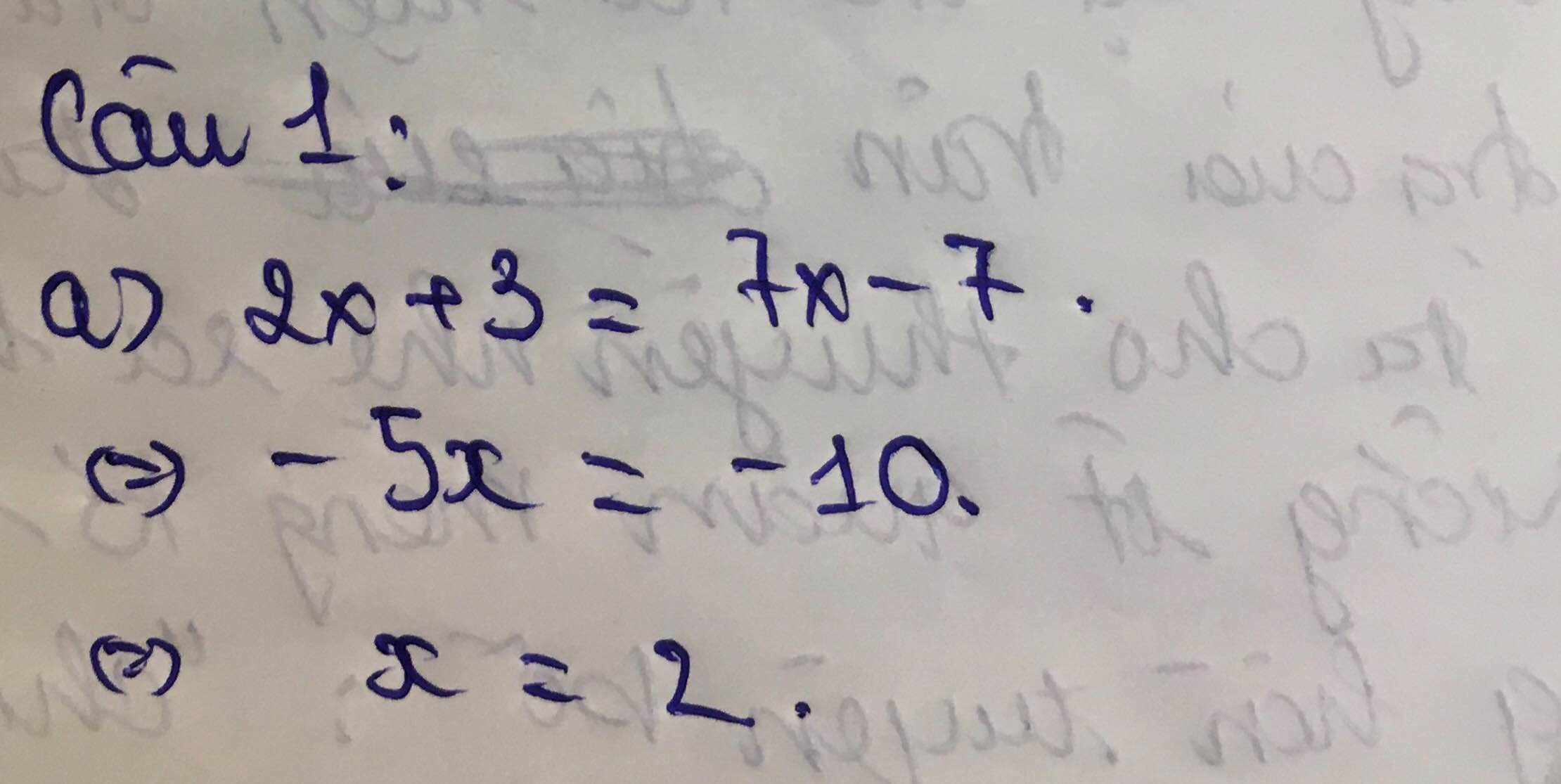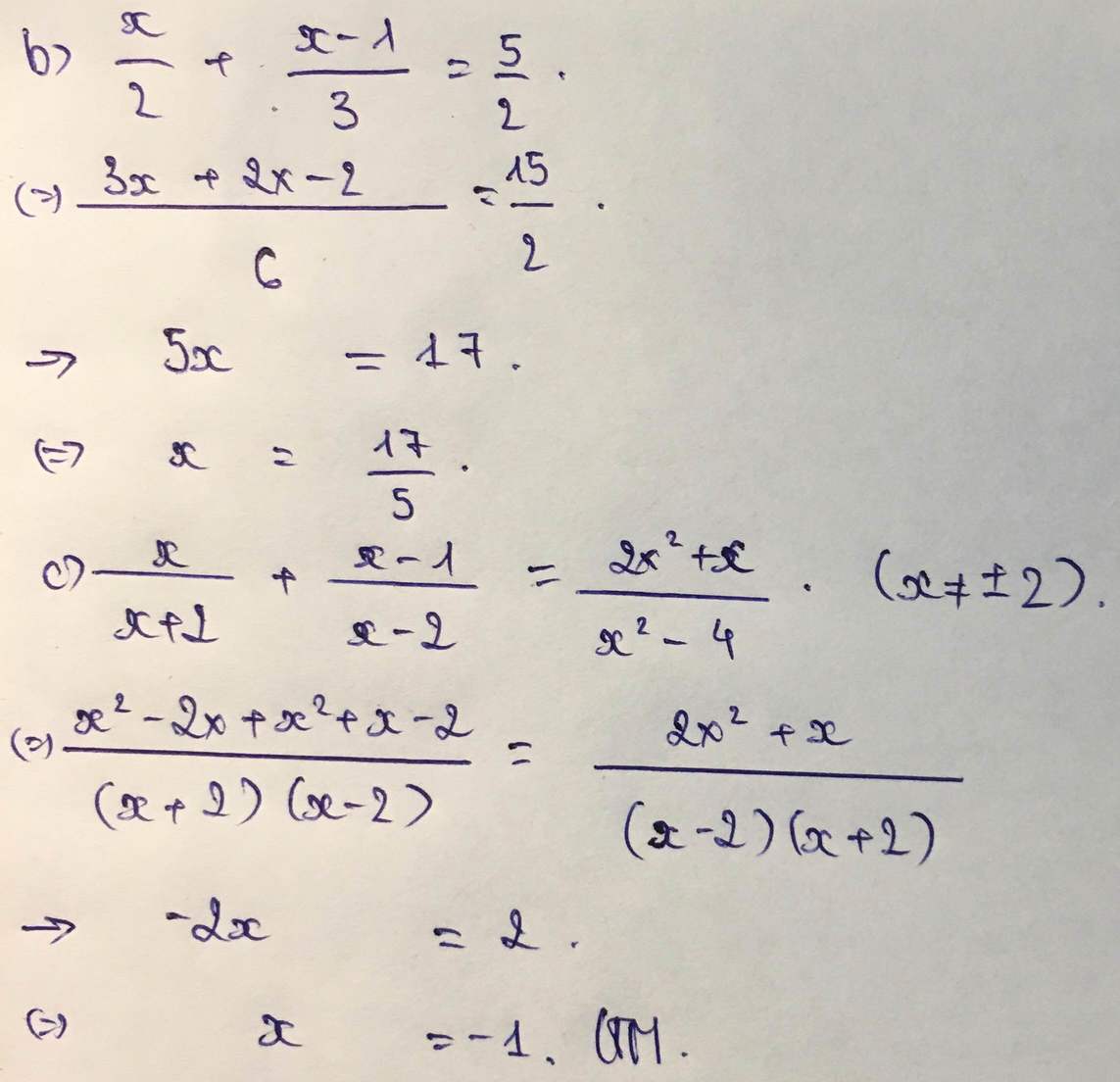xác định hệ số a, b của bất phương trình: \(\dfrac{x}{3}\)-2 >0

Những câu hỏi liên quan
Trong các phương trình sau, phương trình nào là phương trình bậc nhất một ẩn? Xác định các hệ số \(a\) và \(b\) của phương trình bậc nhất một ẩn đó.
a) \(7x + \dfrac{4}{7} = 0\);
b) \(\dfrac{3}{2}y - 5 = 4\);
c) \(0t + 6 = 0\);
d) \({x^2} + 3 = 0\).
a) Phương trình \(7x + \dfrac{4}{7} = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số.
Khi đó, \(a = 7;b = \dfrac{4}{7}\).
b) \(\dfrac{3}{2}y - 5 = 4\)
\(\dfrac{3}{2}y - 5 - 4 = 0\)
\(\dfrac{3}{2}y - 9 = 0\)
Phương trình \(\dfrac{3}{2}y - 9 = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ay + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(y\) là ẩn số.
Khi đó, \(a = \dfrac{3}{2};b = - 9\)
c) Phương trình \(0t + 6 = 0\) không là phương trình bậc nhất một ẩn.
Mặc dù phương trình đã cho có dạng \(at + b = 0\) với \(a\) và \(b\) là các hệ số đã cho nhưng \(a = 0\).
d) Phương trình \({x^2} + 3 = 0\) không là phương trình bậc nhất một ẩn vì không có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số (do có \({x^2}\)).
Đúng 1
Bình luận (0)
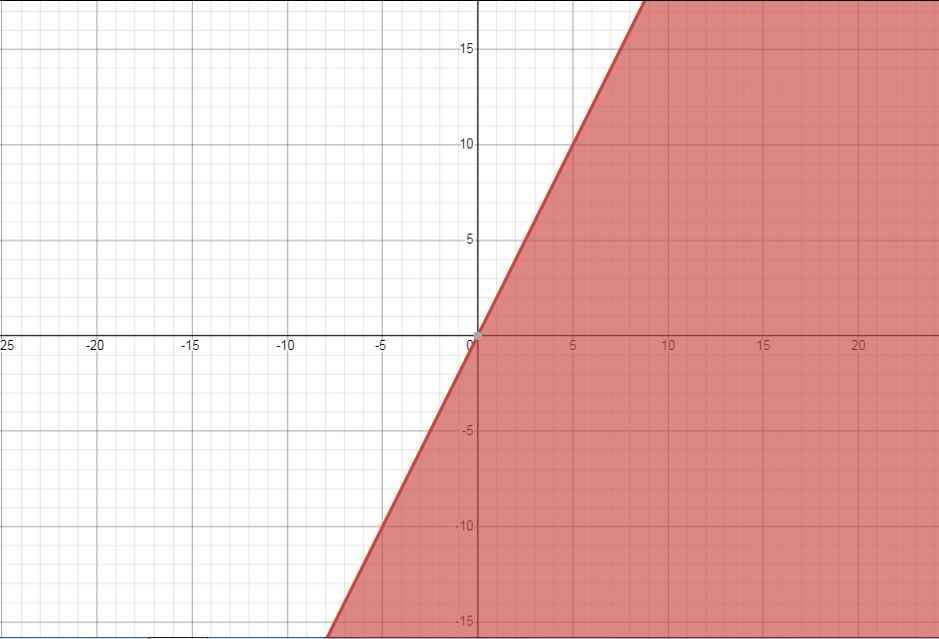
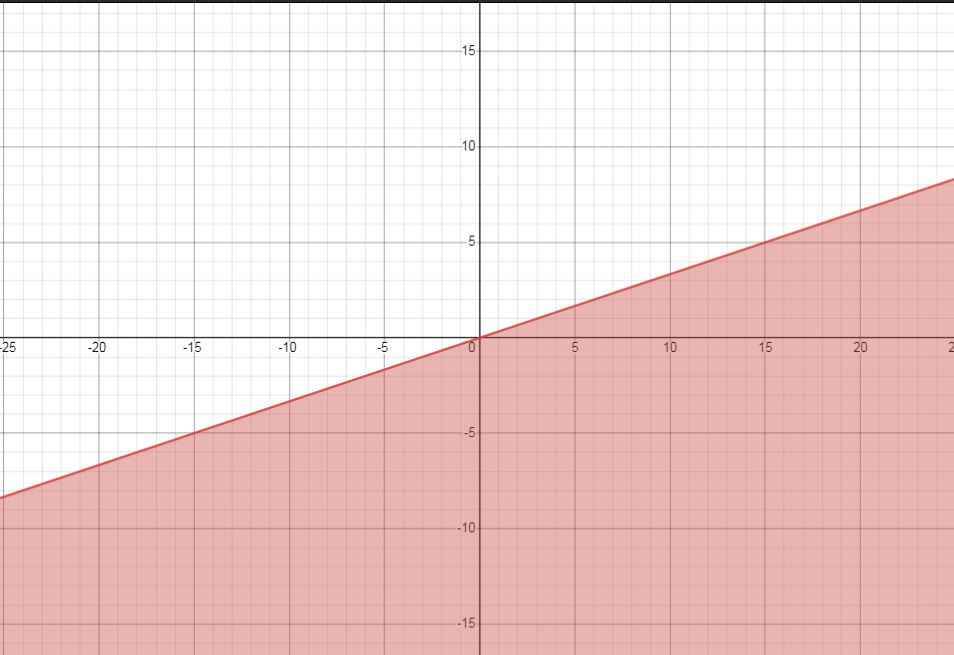
Xác định miền nghiệm của các bất phương trình sau:
a) 2x - y \(\ge0\)
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
\(\Leftrightarrow3x-6y>4x+2y+1\)
\(\Leftrightarrow x+8y+1< 0\)
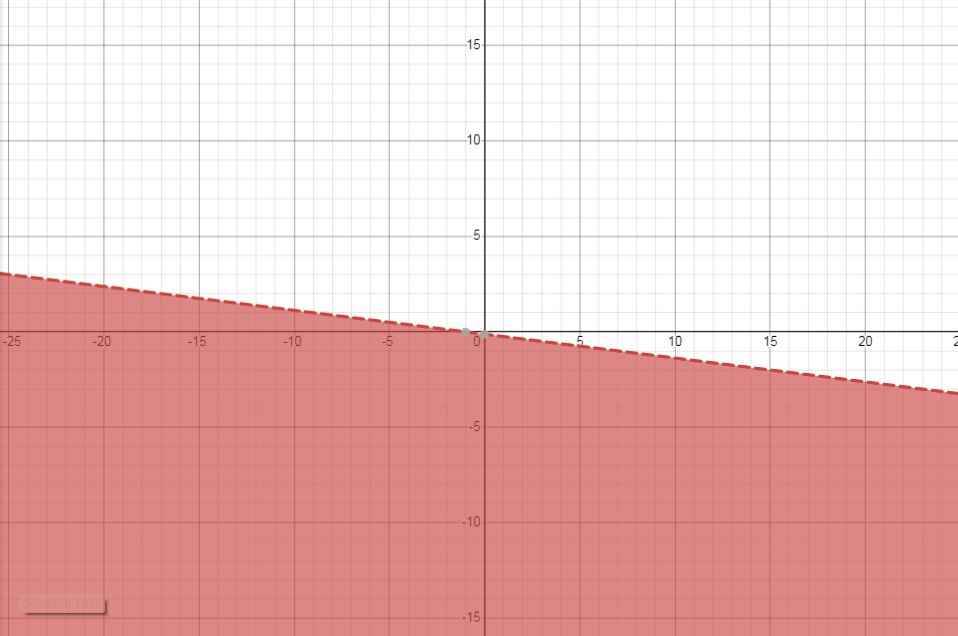
Đúng 0
Bình luận (0)
Trong các phương trình sau phương trình nào là phương trình bậc nhất một ẩn xác định hệ số a,b của phương trình đó 1)0.x-5=0 2)3x²+2=0 3)8x-5=0 4) 3-4x/x=0 5)2x+3=0 6)3/x -5=0
phương trình bậc nhất 1 ẩn:
3)8x-5=0(a=8;b=-5)
5)2x+3=0(a=2;b=3)
Đúng 2
Bình luận (6)
Xác định miền nghiệm của các bất phương trình sau:
a) x - 3y \(\ge0\)
b) \(\dfrac{x-y}{-2}< x+y+1\)
b) \(\dfrac{x-y}{-2}< x+y+1\)
\(\Leftrightarrow x-y>-2x-2y-2\)
\(\Leftrightarrow3x+y+2>0\)
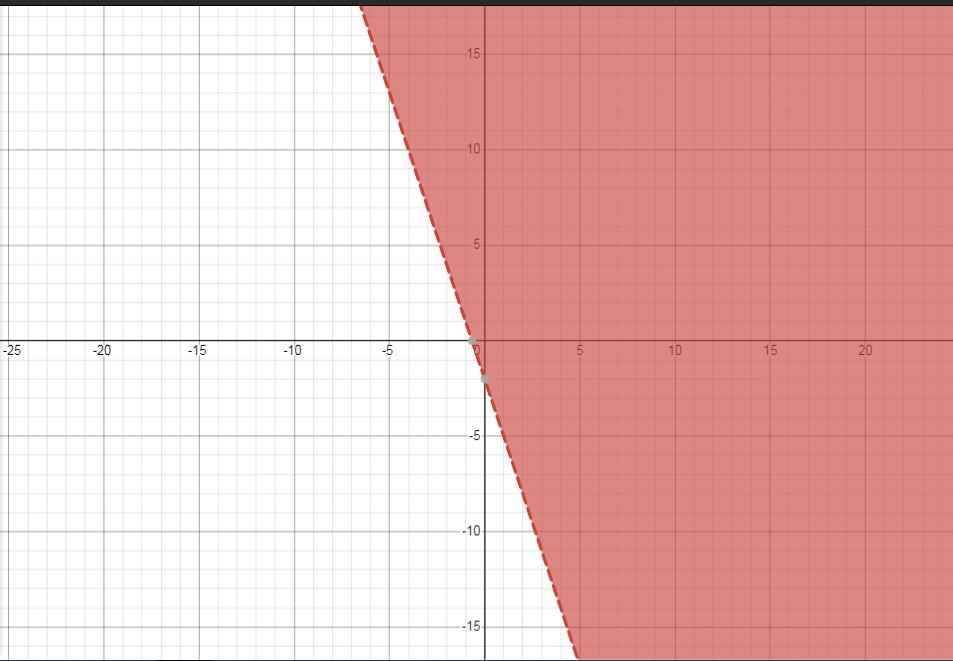
Đúng 1
Bình luận (0)
1. Giải bất phương trình $\left|\dfrac{2x^{2} -x}{3x-4} \right|\ge 1$.
2. Xác định $m$ sao cho hệ bất phương trình $\left\{\begin{aligned}&{x^{2} \le -2x+3} \\ &{\left(m+1\right)x\ge 2m-1} \end{aligned}\right. $ có ngiệm duy nhất.
1. \(\left|\frac{2x^2-x}{3x-4}\right|\ge1\) Điều kiện: \(x\ne\frac{4}{3}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{2x^2-x}{3x-4}\ge1\\\frac{2x^2-x}{3x-4}\le-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{x^2-2x+2}{3x-4}\ge0\\\frac{x^2+x-2}{3x-4}\le0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x>\frac{4}{3}\\x\in(-\infty;-2]U[1;\frac{4}{3})\end{cases}}\Leftrightarrow x\in(-\infty;-2]U[1;+\infty)\backslash\left\{\frac{4}{3}\right\}\)
2.\(\hept{\begin{cases}x^2\le-2x+3\left(1\right)\\\left(m+1\right)x\ge2m-1\left(2\right)\end{cases}}\)
\(\left(1\right)\Leftrightarrow x^2+2x-3\le0\Leftrightarrow-3\le x\le1\)
+) Nếu \(m=-1\) thì (2) vô nghiệm, suy ra \(m\ne-1\)
+) Nếu \(m>-1\) thì \(\left(2\right)\Leftrightarrow x\ge\frac{2m-1}{m+1}\)
Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=1\Leftrightarrow m=2>-1\)
+) Nếu \(m< -1\)thì \(\left(2\right)\Leftrightarrow x\le\frac{2m-1}{m+1}\)
Hệ BPT có nghiệm duy nhất \(\Leftrightarrow\frac{2m-1}{m+1}=-3\Leftrightarrow m=-\frac{2}{5}< -1\)
Vậy \(m=\left\{\frac{-2}{5};2\right\}\)
1. |2x2−x3x−4 |≥1 Điều kiện: x≠43
⇔[
| 2x2−x3x−4 ≥1 |
| 2x2−x3x−4 ≤−1 |
⇔[
| x2−2x+23x−4 ≥0 |
| x2+x−23x−4 ≤0 |
⇔[
| x>43 |
| x∈(−∞;−2]U[1;43 ) |
⇔x∈(−∞;−2]U[1;+∞)\{43 }
2.{
| x2≤−2x+3(1) |
| (m+1)x≥2m−1(2) |
(1)⇔x2+2x−3≤0⇔−3≤x≤1
.
Tập nghiệm :.
2.
Ta có: .
+ Trường hợp 1:
Hệ BPT trở thành: . Hệ luôn đúng với .
Vậy loại.
+ Trường hợp 2:
Hệ BPT trở thành: .
Hệ có nghiệm duy nhất khi (nhận).
+ Trường hợp 3: Hệ BPT trở thành: .
Hệ có nghiệm duy nhất khi (loại). Vậy hệ có nghiệm duy nhất.
Xem thêm câu trả lời
Không giải phương trình, hãy xác định các hệ số a, b, c, tính biệt thức Δ và xác định số nghiệm của mỗi phương trình sau: 7 x 2 - 2 x + 3 = 0
Phương trình bậc hai: 7x2 – 2x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b2 – 4ac = (-2)2 – 4.7.3 = -80 < 0
Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Bài 3. Xác định m để hệ bất phương trình sau có nghiệm, vô nghiệm, có nghiệm duy nhất?a)left{{}begin{matrix}x+m-103m-2-x0end{matrix}right. b)left{{}begin{matrix}x-10mx-30end{matrix}right. c)left{{}begin{matrix}x+4m^2le2mx+13x+22x-1end{matrix}right.d)left{{}begin{matrix}7x-2ge-4x+192x-3m+2 0end{matrix}right. e)left{{}begin{matrix}mx-10left(3m-2right)x-m0end{matrix}right.
Đọc tiếp
Bài 3. Xác định m để hệ bất phương trình sau có nghiệm, vô nghiệm, có nghiệm duy nhất?a)\(\left\{{}\begin{matrix}x+m-1>0\\3m-2-x>0\end{matrix}\right.\) b)\(\left\{{}\begin{matrix}x-1>0\\mx-3>0\end{matrix}\right.\) c)\(\left\{{}\begin{matrix}x+4m^2\le2mx+1\\3x+2>2x-1\end{matrix}\right.\)
d)\(\left\{{}\begin{matrix}7x-2\ge-4x+19\\2x-3m+2< 0\end{matrix}\right.\) e)\(\left\{{}\begin{matrix}mx-1>0\\\left(3m-2\right)x-m>0\end{matrix}\right.\)
Không giải phương trình, hãy các định các hệ số a, b, c, tính biệt thức \(\Delta\) và xác định số nghiệm của mỗi phương trình sau:
a) \(7x^2-2x+3=0;\) b) \(5x^2+2\sqrt{10}x+2=0;\)
c) \(\dfrac{1}{2}x^2+7x+\dfrac{2}{3}=0;\) d) \(1,7x^2-1,2x-2,1=0.\)
Lời giải
a)\(\left\{{}\begin{matrix}a=7\\b=-2\\c=3\end{matrix}\right.\) \(\Rightarrow\Delta'=1-21=-20< 0\Rightarrow\left(a\right)VoN_0\)
(b) \(\left\{{}\begin{matrix}a=5\\b=2\sqrt{10}\\c=2\end{matrix}\right.\) \(\Rightarrow\Delta'=10-10=0\Rightarrow\left(b\right)\) có một nghiệm kép
(c) \(\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=7\\c=\dfrac{2}{3}\end{matrix}\right.\) \(\Rightarrow\Delta=49-4.\dfrac{1}{2}.\dfrac{2}{3}=49-\dfrac{4}{3}=\dfrac{143}{3}>0\) có hai nghiệm phân biệt
(d) \(\left\{{}\begin{matrix}a=1,7\\b=-1,2\\c=-2,1\end{matrix}\right.\) \(\Delta'=0,6^2+2,1.1,7>0\) pt có hai nghiệm phân biệt
Đúng 0
Bình luận (0)
I.trắc nghiệm câu 1: phương trình nào sau đây là phương trình bậc nhất một ẩn:A. x + y 0 B. dfrac{4}{x}+3C. 5 - 4x 0 C.x2 - 4 0câu 2: điều kiện xác định của phương trình dfrac{x+3}{x^2+9}1 là:A. x ≠ 3 B. x ≠ -3C. x ≠ 9 D. x ≠ 3 và x ≠ -3câu 3: x 4 là nghiệm của phương trình nào trong các phương trình sau:A. 2x + 4 6 B. 2x + 1 5 C. x - 4 0 D. x + 4 0câu 4: cho ΔABC kẻ đường thẳng MN // BC (Min AB,Nin AC). Tìm khẳng định đúng:A. dfrac{AM}{AB}dfrac{AN}{NC} B.dfrac...
Đọc tiếp
I.trắc nghiệm
câu 1: phương trình nào sau đây là phương trình bậc nhất một ẩn:
A. x + y = 0 B. \(\dfrac{4}{x}+3\)
C. 5 - 4x = 0 C.x2 - 4 = 0
câu 2: điều kiện xác định của phương trình \(\dfrac{x+3}{x^2+9}=1\) là:
A. x ≠ 3 B. x ≠ -3
C. x ≠ 9 D. x ≠ 3 và x ≠ -3
câu 3: x = 4 là nghiệm của phương trình nào trong các phương trình sau:
A. 2x + 4 = 6 B. 2x + 1 = 5
C. x - 4 = 0 D. x + 4 = 0
câu 4: cho ΔABC kẻ đường thẳng MN // BC (\(M\in AB,N\in AC\)). Tìm khẳng định đúng:
A. \(\dfrac{AM}{AB}=\dfrac{AN}{NC}\) B.\(\)\(\dfrac{AM}{MB}=\dfrac{MN}{BC}\)
C. \(\dfrac{AN}{AC}=\dfrac{MN}{BC}\) D.\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\)
câu 5: ΔABC đường phân giác BD. Khẳng định đúng:
A. \(\dfrac{DA}{DC}=\dfrac{BC}{BA}\) B. \(\dfrac{CD}{CA}=\dfrac{BC}{BA}\)
C. \(\dfrac{BA}{DA}=\dfrac{BC}{DC}\) D. \(\dfrac{BD}{AD}=\dfrac{BD}{DC}\)
câu 6: tập nghiệm của phương trình (x2 + 1)(x - 3) = 0 là:
A. S = {3} B. S = {-1;1;3}
C. S = {-1;3} D. S = \(\varnothing\)
câu 7: phương trình 4x + k = 6 - 3x nhận x = 1 là một nghiệm, khi đó giá trị của k là:
A. k = 1 B. k = 6
C. k = -1 D.k = 7
câu 8: nếu ΔABC và ΔDEF có \(\dfrac{AB}{ED}=\dfrac{BC}{FE}=\dfrac{CA}{DF}\) thì:
A. ΔABC đồng dạng với ΔEDF B. ΔABC đồng dạng với ΔDEF
C. ΔABC đồng dạng với ΔFDE C. ΔABC đồng dạng với ΔEDF
câu 9: một hình thoi có độ dài đường chéo lần lượt là 8cm,6cm thì diện tích hình thoi bằng:
A. 24cm2 B.48cm2
C.14cm2 C.28cm2
câu 10: giá trị của m để phương trình (1 - m)x + 3mx + 5 = 0 có nghiệm duy nhất là:
A. m ≠ -2 B. m ≠ -1
C. m ≠ \(\dfrac{1}{2}\) D. m ≠ \(-\dfrac{1}{2}\)
câu 11: cho ΔABC ∼ ΔMNP theo tỉ số đồng dạng k thì tỉ số \(\dfrac{AB+BC+CA}{MN+NP+MP}\) là:
A. 3k B. k2 C. k D. \(\dfrac{1}{3}k\)
câu 12: nghiệm của phương trình \(\dfrac{X^2-25}{X+5}=0\) là:
A. x = 5 B. X = -5 C. x = \(\pm5\) D. vô nghiệm
II. tự luận:
câu 1: giải các phương trình:
a) 2x + 3 = 7x - 7
b) \(\dfrac{x}{2}+\dfrac{x-1}{3}=\dfrac{5}{2}\)
c) \(\dfrac{x}{x+2}+\dfrac{x-1}{x-2}=\dfrac{2x^2+x}{x^2-4}\)
câu 2: một người đi xe máy từ trung tâm thành phố Nha Trang đến sân bay Cam Ranh với vận tốc 36km/h. Khi về từ sân bay Cam Ranh đến trung tâm thành phố Nha Trang với vận tốc 40km/h, vì thế thời gian về ít hơn thời gian đi là 6 phút. Tính quãng đường từ trung tâm thành phố Nha Trang đến sân bay Cam Ranh?
câu 3: cho hình vẽ sau có DE // BC
a) tính độ dài đoạn DE
b) cho tam giác ABC có AB= 2cm, AC = 3cm, BC= 4cm, có đường phân giác AD. Tính dài của BD và CD