b) \(\dfrac{x-y}{-2}< x+y+1\)
\(\Leftrightarrow x-y>-2x-2y-2\)
\(\Leftrightarrow3x+y+2>0\)
b) \(\dfrac{x-y}{-2}< x+y+1\)
\(\Leftrightarrow x-y>-2x-2y-2\)
\(\Leftrightarrow3x+y+2>0\)

Xác định miền nghiệm của các bất phương trình sau:
a) 2x - y \(\ge0\)
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
Trong các khẳng định sau, khẳng định nào đúng?
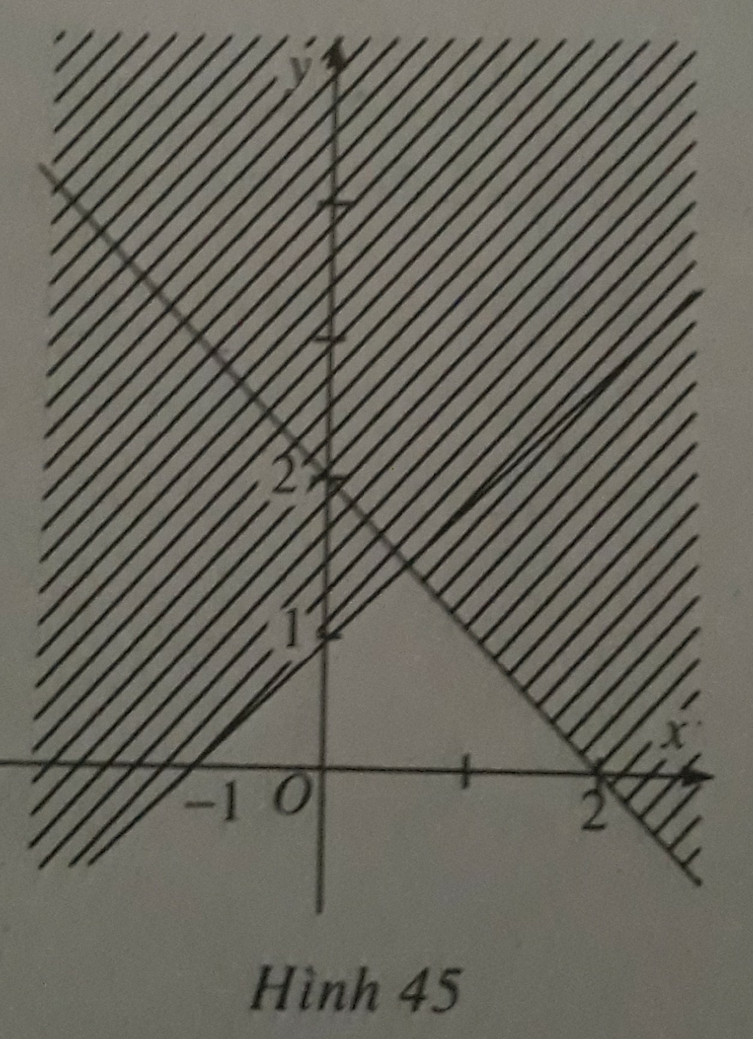
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 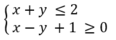 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Gi ải các điểm A, B, C, D miền nghiệm của hệ bất phương trình \(\left[{}\begin{matrix}2x+3y-6< 0\\x\ge0\\2x-3y-1\le0\end{matrix}\right.\)
Trong các điểm có tọa độ cho sau đây, điểm nào thuộc miền nghiệm của bất phương trình x + 3 y - 2 ≥ 0 2 x + y + 1 ≤ 0 ?
A. (0;1)
B.(-1;1)
C. (1;3)
(-1:0)
Trong các điểm có tọa độ cho sau đây, điểm nào thuộc miền nghiệm của bất phương trình x + 3 y - 2 ≥ 0 2 x + y + 1 ≤ 0 ?
A. (0;1)
B. (-1;1)
C. (1;3)
D. (-1;0)
Điểm M(2;-3) thuộc miền nghiệm của bất phương trình nài dưới đây
A. x+2y ≥7
B. x+3y >2
C. 4x+y >6
D. 2x-y <7
Trong các bất phương trình sau bất phương trình nào không là bất phương trình bậc nhất hai ẩn
A. 2x+3y-5>0
B. x(y+3)-5\(\le0\)
C. 2x-5\(\ge0\)
D. y<0
Miền nghiệm của hệ bất phương trình \(\left[{}\begin{matrix}-x+4y>0\\-2x+y< 0\\x+3y< 7\\x< 3\end{matrix}\right.\) là
A. Một nửa mặt phẳng
B, Miền tam giác
C, Miền tứ giác
D. Miền ngũ giác
Biểu diễn hình học tập nghiệm của các bất phương trình bậc nhất hai ẩn sau:
a,\(\hept{\begin{cases}2x-1\le0\\-3x+5\le0\end{cases}}\)
b,\(\hept{\begin{cases}3-y< 0\\2x-3y+1>0\end{cases}}\)
c,\(\hept{\begin{cases}x-2y< 0\\x+3y>-2\end{cases}}\)
d,\(\hept{\begin{cases}3x-2y-6\ge0\\2\left(x-1\right)+\frac{3y}{2}\le4\\x\ge0\end{cases}}\)
e,\(\hept{\begin{cases}x-y>0\\x-3y\le-3\\x+y>5\end{cases}}\)
f,\(\hept{\begin{cases}x-3y< 0\\x+2y>-3\\y+x< 2\end{cases}}\)