Chọn C
Miền nghiệm của hệ bất phương trình là miền tứ giác `ABOC` với `A(-6;-2)`, `B(-2;2)` và `C(0;-2)`
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x+y\le10\\-3\le x\le3\\-3\le y\le3\end{matrix}\right.\) là:
A. Một nửa mặt phẳng
B. Miền tam giác
C. Miền tứ giác
D. Miền ngũ giác
Gi ải các điểm A, B, C, D miền nghiệm của hệ bất phương trình \(\left[{}\begin{matrix}2x+3y-6< 0\\x\ge0\\2x-3y-1\le0\end{matrix}\right.\)
Biểu diễn miền nghiệm của hệ bất phương trình sau trên mặt phẳng tọa độ:
\(\left\{{}\begin{matrix}y-x< -1\\x>0\\y< 0\\\end{matrix}\right.\)
Gi á trị nhỏ nhất của biểu thức F( x;y ) = y - x thuộc miền nghiệm của hệ bất phương trình
\(\left\{{}\begin{matrix}y-2x\le2\\2y-x\ge4\\x+y\le5\end{matrix}\right.\) là
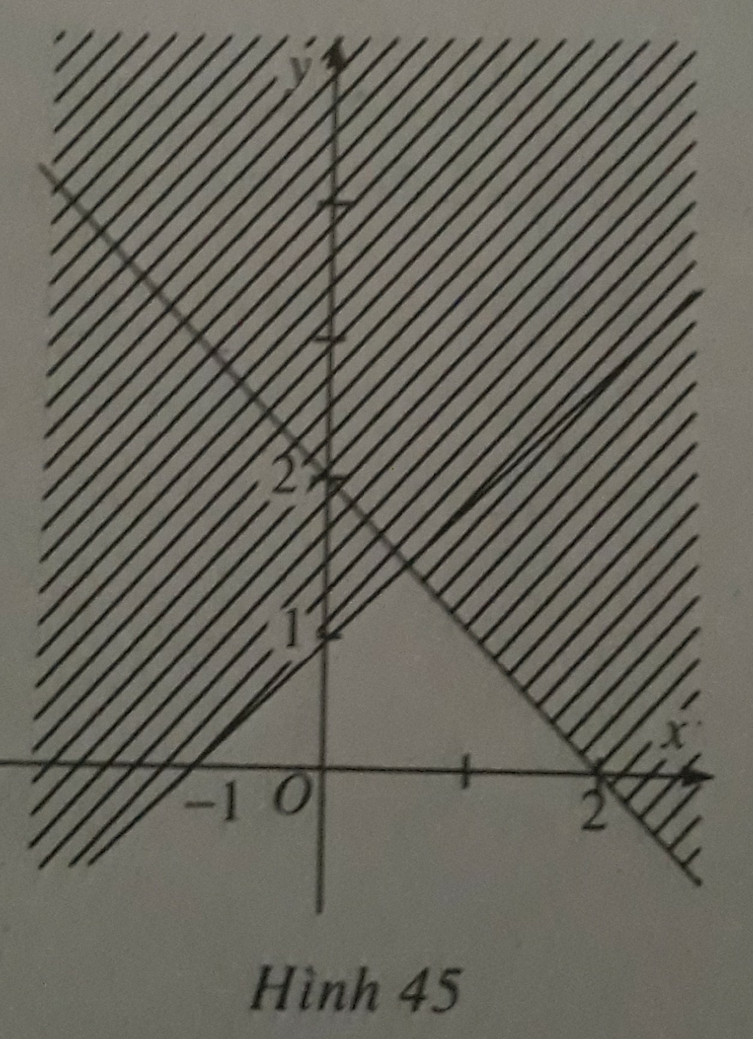
Trong các khẳng định sau, khẳng định nào đúng?A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2. B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trìnhvà (x; y) (-1; 1) là một nghiệm của hệ. C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và (x; y) (-2; 1) là một nghiệm của hệ. D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và...
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng?
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình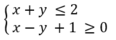 
và (x; y) = (1; 0) là một nghiệm của hệ.
Tìm m để hệ bất phương trình \(\left\{{}\begin{matrix}2x+m< 0\\3x^2-x-4\le0\end{matrix}\right.\)vô nghiệm
10 tháng 1 2022 lúc 20:39
Giải hệ phương trình
\(\left\{{}\begin{matrix}3x-4y+1=0\\xy=3\left(x+y\right)-9\end{matrix}\right.\)
Bài 2 (1 điểm)
a) Biểu diễn miền nghiệm của hệ bpt $left{ begin{aligned} & xge 0 & 0le yle 4 & x+yle 7 & x+3yle 15 end{aligned} right.$.
b) Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một sản phẩm loại I cần dùng $1$ máy nhóm A và $1$ máy nhóm B. Để sản xuất ra một sản phẩm loại $2$ cần dùng $1$ máy nhóm A, $3$ máy nhóm B và $2$ máy nhóm C. Nhà máy có $7$ máy nhóm A, $15$ máy nhóm B, $8$ máy nhóm C. Biết một sản phẩm loại I lãi $10$ nghìn đồng, một sản...
Đọc tiếp
Bài 2 (1 điểm)
a) Biểu diễn miền nghiệm của hệ bpt $\left\{ \begin{aligned} & x\ge 0 \\ & 0\le y\le 4 \\ & x+y\le 7 \\ & x+3y\le 15 \\ \end{aligned} \right.$.
b) Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một sản phẩm loại I cần dùng $1$ máy nhóm A và $1$ máy nhóm B. Để sản xuất ra một sản phẩm loại $2$ cần dùng $1$ máy nhóm A, $3$ máy nhóm B và $2$ máy nhóm C. Nhà máy có $7$ máy nhóm A, $15$ máy nhóm B, $8$ máy nhóm C. Biết một sản phẩm loại I lãi $10$ nghìn đồng, một sản phẩm loại II lãi $15$ nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi là cao nhất.
Tìm m để hệ bất phương trình \(\left\{{}\begin{matrix}x^2-1\le0\\x-m>0\end{matrix}\right.\)có nghiệm