b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
\(\Leftrightarrow3x-6y>4x+2y+1\)
\(\Leftrightarrow x+8y+1< 0\)
b) \(\dfrac{x-2y}{2}>\dfrac{2x+y+1}{3}\)
\(\Leftrightarrow3x-6y>4x+2y+1\)
\(\Leftrightarrow x+8y+1< 0\)

Xác định miền nghiệm của các bất phương trình sau:
a) x - 3y \(\ge0\)
b) \(\dfrac{x-y}{-2}< x+y+1\)
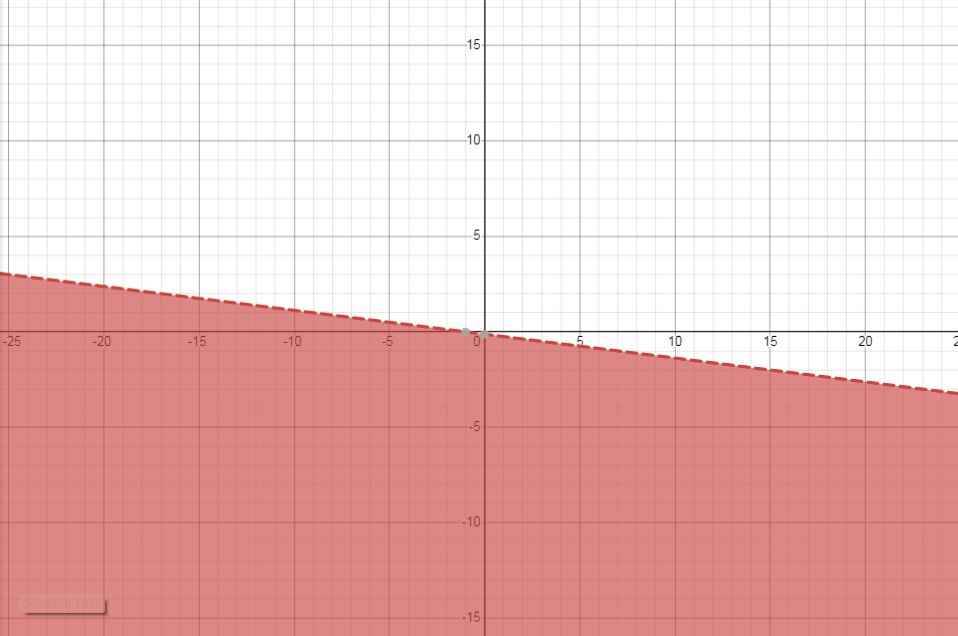
Hình 43 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình nào sau đây?
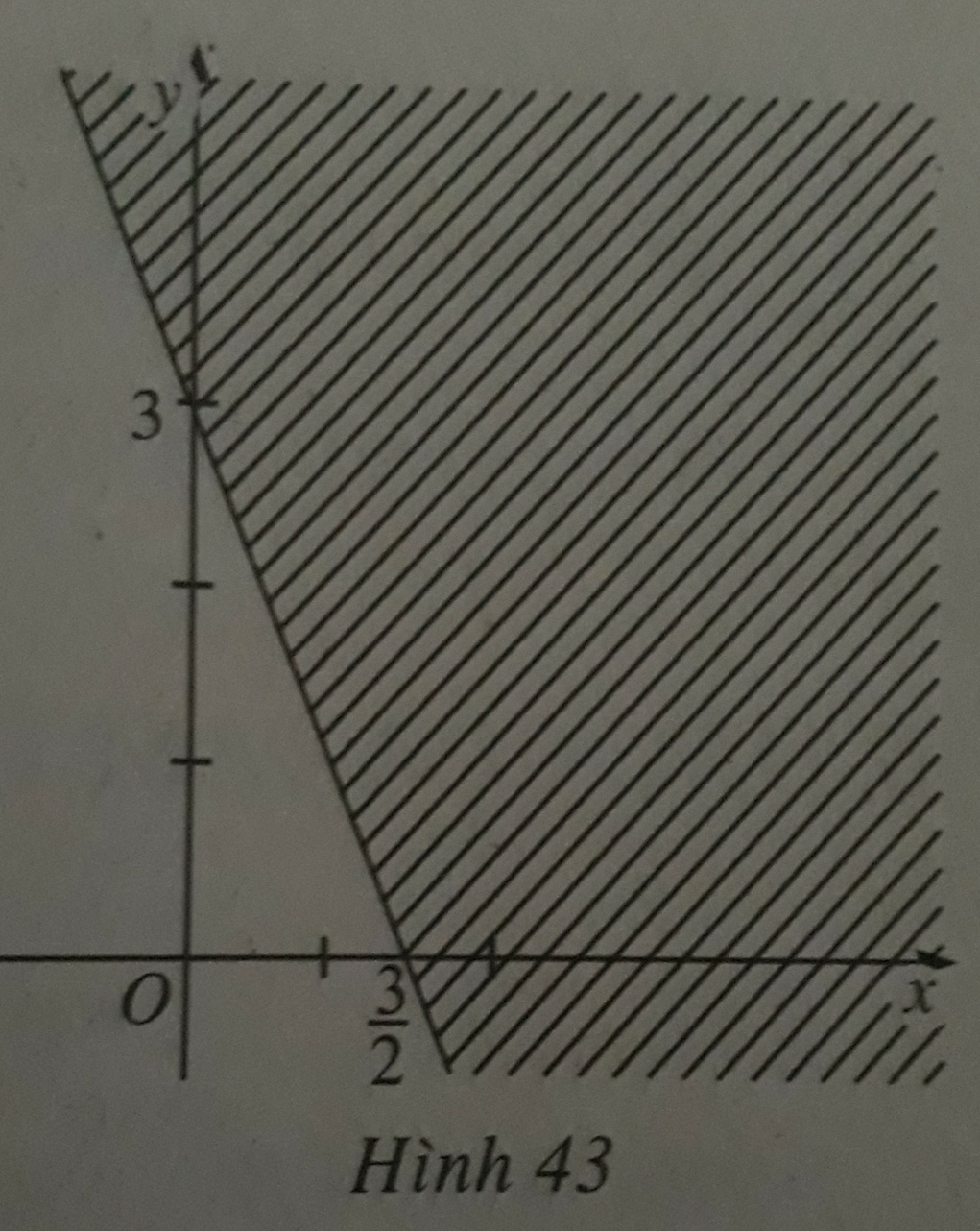
A. x + 2y > 3
B. 2x + y ≤ 3
C. 2x + y < 3
D. x + y - 3 ≤ 0
Trong các khẳng định sau, khẳng định nào đúng?
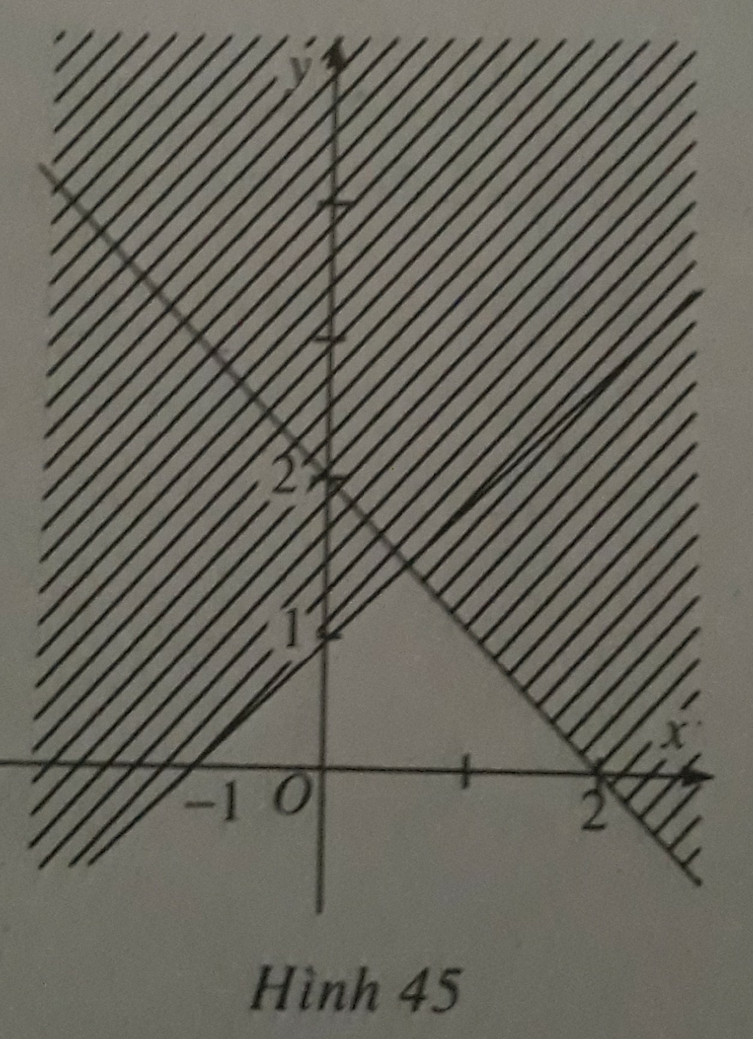
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 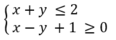 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Gi ải các điểm A, B, C, D miền nghiệm của hệ bất phương trình \(\left[{}\begin{matrix}2x+3y-6< 0\\x\ge0\\2x-3y-1\le0\end{matrix}\right.\)
Điểm M(2;-3) thuộc miền nghiệm của bất phương trình nài dưới đây
A. x+2y ≥7
B. x+3y >2
C. 4x+y >6
D. 2x-y <7
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
Giải các bất phương trình sau
a/ (x+1).(x-1).(3x-6)>0
b/ \(\dfrac{x+3}{x-2}\le0\)
c/ \(\dfrac{\left(2x-5\right).\left(x+2\right)}{-4x+3}\ge0\)
d/ \(\dfrac{2x-5}{3x+2}< \dfrac{3x+2}{2x-5}\)
e/ \(\dfrac{2x^2+x}{1-2x}\ge1-x\)
f/ \(\dfrac{\left(2+x\right)^5.\left(x+1\right).\left(3-x\right)^{11}}{\left(2-x\right).\left(1-x\right)^{20}}\le0\)
Giải bất phương trình sau: \(\dfrac{1-x^2-2x}{x^2+x-2}\ge0\)
Giải các bất phương trình sau:
a)\(\left(x^2+3x-4\right)\left(3-2x\right)\)<0
b) \(\dfrac{x^2+3x+4}{x^2-2}\ge0\)
c) \(\dfrac{x\left(x^2+4x+4\right)}{x^2-1}\ge0\)