Cho \(A=\dfrac{n-5}{n+1}\)\(\left(n\in Z;n\ne1\right)\). Tìm n để A là phân số tối giản.

Những câu hỏi liên quan
Cho A=\(\dfrac{n+2}{n-5}\left(n\in z;n\ne5\right)\) Tìm n để A ϵ Z
Ta có : \(A=\dfrac{n+2}{n-5}\)
\(\Rightarrow A=\dfrac{n-5+7}{n-5}=\dfrac{n-5}{n-5}+\dfrac{7}{n-5}\)
\(\Rightarrow A=1+\dfrac{7}{n-5}\)
Để \(A\in Z\Leftrightarrow\dfrac{7}{n-5}\in Z\)
\(\Leftrightarrow\left(n-5\right)\inƯ\left(7\right)\)
mà \(Ư\left(7\right)=\left(\pm1;\pm7\right)\)
\(\Rightarrow n\in\left(6;4;12;-2\right)\)
\(Vậy...\)
Đúng 1
Bình luận (0)
Cho Biểu Thức : \(A=\dfrac{2n+1}{n-3}+\dfrac{3n-5}{n-3}-\dfrac{4n-5}{n-3}\left(n\in Z,n\ne3\right)\)
a) Tìm n để A nhận giá trị nguyên
b) Tìm n để A là p/s tối giản
.
a, \(A=\dfrac{5n-4-4n+5}{n-3}=\dfrac{n+1}{n-3}=\dfrac{n-3+4}{n-3}=1+\dfrac{4}{n-3}\Rightarrow n-3\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
| n-3 | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 4 | 2 | 5 | 1 | 7 | -1 |
Đúng 2
Bình luận (0)
a.\(A=\dfrac{2n+1}{n-3}+\dfrac{3n-5}{n-3}-\dfrac{4n-5}{n-3}\)
\(A=\dfrac{2n+1+3n-5-4n+5}{n-3}\)
\(A=\dfrac{n+1}{n-3}\)
\(A=\dfrac{n-3}{n-3}+\dfrac{4}{n-3}\)
\(A=1+\dfrac{4}{n-3}\)
Để A nguyên thì \(\dfrac{4}{n-3}\in Z\) hay \(n-3\in U\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\)
n-3=1 --> n=4
n-3=-1 --> n=2
n-3=2 --> n=5
n-3=-2 --> n=1
n-3=4 --> n=7
n-3=-4 --> n=-1
Vậy \(n=\left\{4;2;5;7;1;-1\right\}\) thì A nhận giá trị nguyên
b.hemm bt lèm:vv
Đúng 4
Bình luận (2)
Cho phân số :\(A=\dfrac{3n-5}{2n+1}\left(n\in Z;n\ne\dfrac{-1}{2}\right)\)
a) Tìm n để A là phân số tối giản.
b) Tìm GTLN, GTNN của A.
Cho \(n\in Z^+;n>1\)
Đặt \(P=\left(1-\dfrac{1}{1+2}\right)\left(1-\dfrac{1}{1+2+3}\right)....\left(1-\dfrac{1}{1+2+...+n}\right)\)
Tìm n để \(\dfrac{1}{P\left(n\right)}\in N\)
Lời giải:
Xét một thừa số tổng quát:
\(1-\frac{1}{1+2+...+n}=1-\frac{1}{\frac{n(n+1)}{2}}=1-\frac{2}{n(n+1)}\)
\(1-\frac{1}{1+2+...+n}=\frac{n^2+n-2}{n(n+1)}=\frac{(n-1)(n+2)}{n(n+1)}\)
Do đó:
\(P_n=\left(1-\frac{1}{1+2}\right)\left(1-\frac{1}{1+2+3}\right)....\left(1-\frac{1}{1+2+...+n}\right)\)
\(P_n=\frac{1.4}{2.3}.\frac{2.5}{3.4}.\frac{3.6}{4.5}....\frac{(n-1)(n+2)}{n(n+1)}\)
\(P_n=\frac{(1.2.3...(n-1))(4.5.6...(n+2))}{(2.3.4...n)(3.4.5..(n+1))}\)
\(P_n=\frac{1}{n}.\frac{n+2}{3}=\frac{n+2}{3n}\Rightarrow \frac{1}{P_n}=\frac{3n}{n+2}\)
Để \(\frac{1}{P_{n}}\in\mathbb{N}\Rightarrow \frac{3n}{n+2}\in\mathbb{N}\)
\(\Leftrightarrow 3n\vdots n+2\)
\(\Leftrightarrow 3(n+2)-6\vdots n+2\)
\(\Leftrightarrow 6\vdots n+2\)
\(\Rightarrow n+2=6\) do \(n+2>3\forall n>1\)
\(\Leftrightarrow n=4\)
Vậy \(n=4\)
Đúng 0
Bình luận (0)
Cho phân số: \(A=\dfrac{3n-5}{2n}+1\left(n\in Z;n\ne\dfrac{-1}{2}\right)\)
a) Tìm n để a là phân số có thể rút gon được.
b) Tìm GTLN, GTNN của A.
1: cho \(A=\dfrac{2n+3}{n-1}\)
a, tìm điều kiện để A là số hữu tỉ
b, tìm \(n\in Z\) để A có giá trị là số nguyên
2: cho \(x=\dfrac{a}{n},y=\dfrac{b}{n}\left(a,b,n\in Z;n>0;x< y\right)\)
chứng tỏ rằng nếu \(Z=\dfrac{a+b}{2n}\) thì x < z < y
1.a) để A là số hữu tỉ thì 2n+3 nguyên và n - 1 khác 0
từ hai điều kiện trên suy ra n nguyên và n khác 1
b) để A nguyên thì 2n+3 ⋮ n - 1
⇒ 2(n - 1) +5 ⋮ n - 1
⇒ 5 ⋮ n - 1
⇒n ∈ {-4; 0; 2; 6}
2. x < y ⇔ \(\dfrac{a}{n}< \dfrac{b}{n}\)
\(\Rightarrow\dfrac{2a}{2n}< \dfrac{a+b}{2n}< \dfrac{2b}{2n}\Leftrightarrow x< z< y\)
Đúng 0
Bình luận (0)
Tính tổng đại số
\(A=\dfrac{1}{2}-\dfrac{1}{3}-\dfrac{2}{3}+\dfrac{1}{4}+\dfrac{2}{4}+\dfrac{3}{4}-\dfrac{1}{5}-\dfrac{2}{5}-\dfrac{3}{5}-\dfrac{4}{5}+...+\dfrac{1}{10}+\dfrac{2}{10}+...+\dfrac{9}{10}\)
\(B=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{2}{3}+\dfrac{1}{4}+\dfrac{2}{4}+\dfrac{3}{4}+...+\dfrac{1}{n}+\dfrac{2}{n}+...+\dfrac{n-1}{n}\)\(\left(n\in Z,n\ge2\right)\)
Cho phân số \(A=\dfrac{n+1}{n-3},\left(n\in\mathbb{Z};n\ne3\right)\)
Tìm n để A là phân số tối giản ?
\(A=\dfrac{n+1}{n-3}=\dfrac{n-3+4}{n-3}=\dfrac{n-3}{n-3}+\dfrac{4}{n-3}=1+\dfrac{4}{n-3}\)
Để A là p/s tối giản thì \(\dfrac{4}{n-3}\) phải là p/s tối giản
\(=>n-3\) là số lẻ \(\Leftrightarrow n\) là số chẵn
Vậy \(n=2k\left(k\in Z\right)\)
Đúng 0
Bình luận (0)
Có thể có phân số \(\dfrac{a}{b},\left(a,b\in\mathbb{Z},b\ne0\right)\) sao cho :
\(\dfrac{a}{b}=\dfrac{a.m}{b.n},\left(m,n\in\mathbb{Z};m,n\ne0,m\ne n\right)\) hay không ?
Có thể có phân số a/b (a, b ∈ Z, b ≠ 0) sao cho:
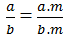
Vì 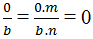
Đúng 0
Bình luận (0)






















