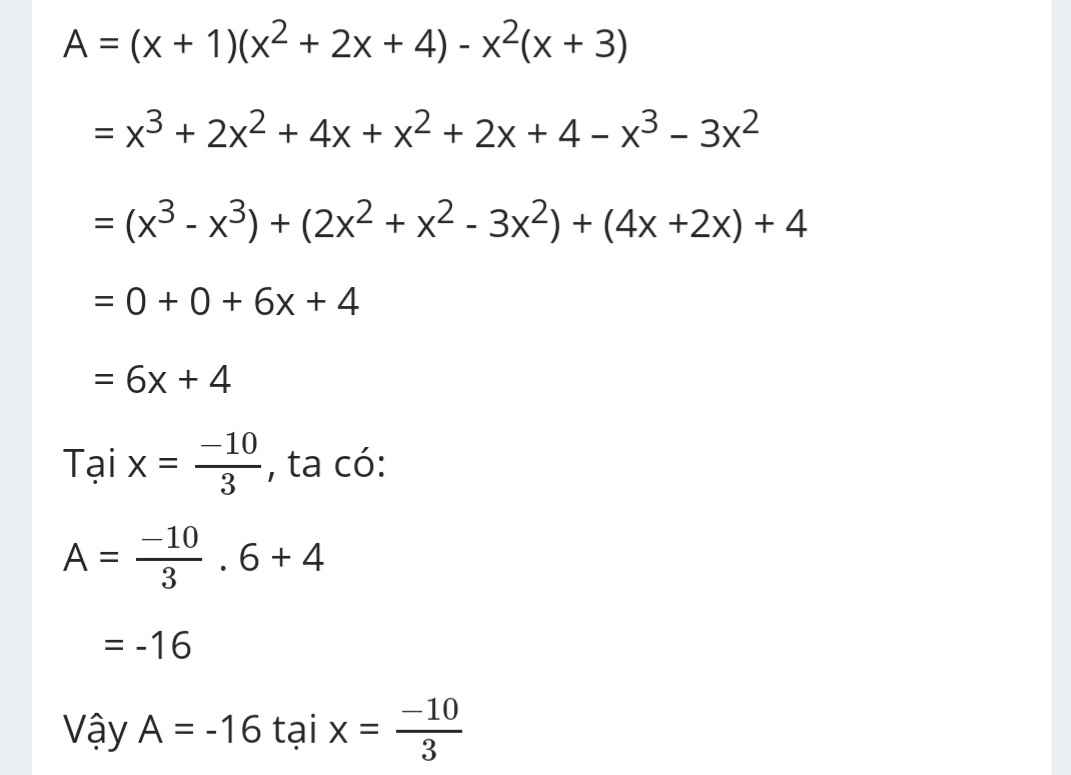tại sao 4x^4+36x^2+81-36x^2=(2x^2+9)^2-36x^2

Những câu hỏi liên quan
ohaan tích đa thức sau thành nhân tữ 4x^4+36x^2+81-36x^2
\(4x^4+36x^2+81-36x^2=\left(4x^4+36x^2+81\right)-36x^2=\left(2x^2+9\right)^2-36x^2=\left(2x^2+9+6x\right)\left(2x^2+9-6x\right)\)
Đúng 0
Bình luận (0)
\(4x^4+36x^2+81-36x^2\)
\(=\left(2x-9\right)^2-\left(6x\right)^2=\left(2x^2+9+6x\right)\left(2x^2-6x+9\right)=\left(2x^2+6x+9\right)\left(2x^2-6x+9\right)\)
Đúng 0
Bình luận (0)
\(4x^4+36x^2+81-36x^2=\left(2x^2\right)^2+9^2=\left(2x^2\right)^2+36x^2+9^2-\left(6x\right)^2=\left(2x^2+9\right)^2-\left(6x\right)^2=\left(2x^2-6x+9\right)\left(2x^2+6x+9\right)\)
Đúng 0
Bình luận (0)
Điền vào chỗ trống cho thích hợp;
a) x^2 + 4x + 4 = ...
b) (x-3)(x^2 + 3x+ 9 )= ...
c) x^2 -1=...
d) 36x^2 + 36x +9 =...
a) \(x^2+4x+4=\left(x+2\right)^2\)
b) \(\left(x-3\right)\left(x^2+3x+9\right)=x^3-27\)
c) \(x^2-1=\left(x-1\right)\left(x+1\right)\)
d) \(36x^2+36x+9=9\left(2x+1\right)^2\)
Đúng 0
Bình luận (0)
Min ra kết quả lun nha bn!
a, (x+2)2
b, x3-33
c, (x-1)(x+1)
d, 9.(2x+1)2
Đúng 0
Bình luận (0)
cách bạn ghi rõ cách giải ra giúp mình đuuơcj ko
Đúng 0
Bình luận (0)
(x+1)(x^2+2x+4)-x^2(x+3) với x=-10/3
6x(2x-7)-(3x-5)(4x+7) tại x=-2
(x-3)(x+3)-(x+2)(x-1) tại x=1/3
Cho\(A=\sqrt{4x^2-4x+1}+\sqrt{4x^2-36x+81}với\frac{1}{2}\le x\le\frac{9}{2}.\)
Rút Gọn A
\(A=\sqrt{4x^2-4x+1}+\sqrt{4x^2-36x+81}\)
\(=\sqrt{\left(2x\right)^2-2.2x.1+1^2}+\sqrt{\left(2x\right)^2-2.2x.9+9^2}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-9\right)^2}\)
\(=\left|2x-1\right|+\left|2x-9\right|\)
\(=2x-1+9-2x=8\)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
1)4x^2+2x-36x-9y+81y^2
2)x^4-5x^2+4
2) \(x^4-5x^2+4\)
\(=x^4-x^2-4x^2+4\)
\(=x^2\left(x^2-1\right)-4\left(x^2-1\right)\)
\(=\left(x^2-1\right)\left(x^2-4\right)\)
\(=\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)\)
Đúng 2
Bình luận (0)
$\sqrt{25x^2+80x+64}+\sqrt{9x^2-6x+1}=\sqrt{4x^2+36x+81}$
Giai phuong trinh
x^2-25=..... 16x^2+8x+1=...... 36x^2-36x+9=.......
\(9X^2+6X+1\)
\(36X^2+36X+9\)
\(X^3+27\)
a) \(\sqrt{4x+20}+\sqrt{x+5}-\dfrac{1}{3}\sqrt{9x+45}=4\)
b) \(\sqrt{36x-36}-\sqrt{9x-9}-\sqrt{4x-4}=16-\sqrt{x-1}\)
c) \(\sqrt{x^2+6x-9}-2\sqrt{x^2-2x+1}+\sqrt{x^2}=0\)
a: =>2*căn x+5+căn x+5-1/3*3*căn x+5=4
=>2*căn(x+5)=4
=>căn (x+5)=2
=>x+5=4
=>x=-1
b: =>\(6\sqrt{x-1}-3\sqrt{x-1}-2\sqrt{x-1}+\sqrt{x-1}=16\)
=>2*căn x-1=16
=>x-1=64
=>x=65
Đúng 2
Bình luận (0)
c, \(\sqrt{\left(x-3\right)^2}-2\sqrt{\left(x-1\right)^2}+\sqrt{x^2}=0\\ \Leftrightarrow\left|x-3\right|-2\left|x-1\right|+\left|x\right|=0\left(1\right)\)
TH1: \(x\ge3\)
\(\left(1\right)\Rightarrow x-3-2x+2+x=0\\ \Leftrightarrow-1=0\left(loại\right)\)
TH2: \(2\le x< 3\)
\(\left(1\right)\Rightarrow3-x-2x+2+x=0\\ \Leftrightarrow-2x=-5\\ \Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)
TH3: \(0\le x< 2\)
\(\left(1\right)\Rightarrow3-x+2x-2+x=0\\ \Leftrightarrow2x=1\\ \Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
TH4: \(x< 0\)
\(\left(1\right)\Rightarrow3-x+2x-2-x-=0\\ \Leftrightarrow1=0\left(loại\right)\)
Vậy \(x\in\left\{\dfrac{1}{2};\dfrac{5}{2}\right\}\)
Đúng 1
Bình luận (0)