Moi nguoi giai giup minh voi

Những câu hỏi liên quan
Mọi người giải giúp mình với🥺
a) Điện trở tương đương của đoạn mạch :
\(R_{tđ}=R_1+R_2+R_3=10+20+30=60\left(\Omega\right)\)
b) Có : \(I=\dfrac{U}{R}=\dfrac{24}{60}=0,4\left(A\right)\)
⇒ \(I=I_1=I_2=I_3=0,4\left(A\right)\) ( vì R1 nt R2 nt R3)
Hiệu điện thế của U1 , U2 và U3
\(\left\{{}\begin{matrix}U_1=I_1.R_1=0,4.10=4\left(V\right)\\U_2=I_2.R_2=0,4.20=8\left(V\right)\\U_3=I_3.R_3=0,4.30=12\left(V\right)\end{matrix}\right.\)
Chúc bạn học tốt
Đúng 3
Bình luận (0)
\(R_{tđ}=R_1+R_2+R_3=10+20+30=60\Omega\)
\(I_m=\dfrac{U_m}{R}=\dfrac{24}{60}=0,4A\)\(\Rightarrow I_1=I_2=I_3=I_m=0,4A\)
\(U_1=0,4\cdot10=4V\)
\(U_2=0,4\cdot20=8V\)
\(U_3=0,4\cdot30=12V\)
Đúng 1
Bình luận (0)
Mình bí quá. Mong mọi người giúp mình với 🥺🥺
Mọi người ơi giúp mình với
Mình đang cần gấp lắm 😭😭😭😭😭😭🥺🥺🥺🥺🥺
Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.
Đúng 0
Bình luận (0)
Mọi người ơi giúp mình với🥺
Bài 2:
a: \(P=\sqrt{a}+2+\sqrt{a}+2=2\sqrt{a}+4\)
b: Để P=a+1 thì \(a-2\sqrt{a}-3=0\)
hay a=9
Đúng 1
Bình luận (0)
\(2,\\ a,P=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{2-\sqrt{a}}=\sqrt{a}+2+2+\sqrt{a}=2\sqrt{a}+4\\ b,P=a+1\Leftrightarrow a-2\sqrt{a}-3=0\\ \Leftrightarrow\left(\sqrt{a}+1\right)\left(\sqrt{a}-3\right)=0\\ \Leftrightarrow\sqrt{a}=3\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a=9\left(tm\right)\\ 3,\\ a,ĐK:x\ge0;x\ne4\\ b,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+2}\\ c,P=2\Leftrightarrow2\sqrt{x}+4=2\sqrt{x}\\ \Leftrightarrow0\sqrt{x}=-4\Leftrightarrow x\in\varnothing\)
Đúng 1
Bình luận (0)
Mọi người giải giúp mình vs ạ. Chiều nay mình phải nộp r 🥺Cảm ơn mn nhiều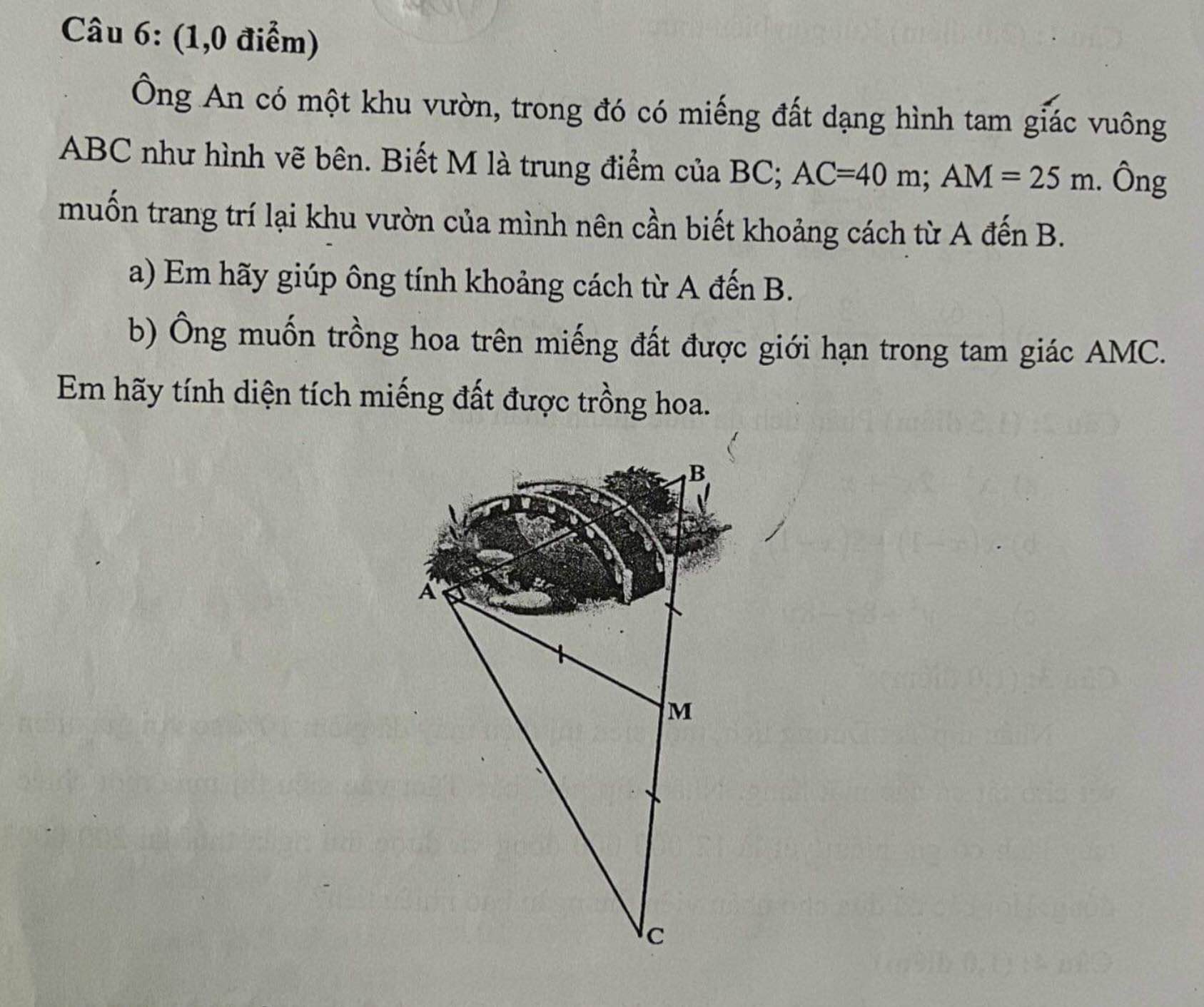
Tam giác ABC vuông tại A có AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC\Rightarrow BC=2AM=50\left(m\right)\)
a. Áp dụng định lý Pitago:
\(AB=\sqrt{BC^2-AC^2}=30\left(m\right)\)
b. Kẻ \(MH\perp AC\Rightarrow MH||AB\) (cùng vuông góc AC)
Mà M là trung điểm BC \(\Rightarrow MH\) là đường trung bình tam giác ABC
\(\Rightarrow MH=\dfrac{1}{2}AB=15\left(m\right)\)
\(\Rightarrow S_{AMC}=\dfrac{1}{2}MH.AC=\dfrac{1}{2}.15.40=300\left(m^2\right)\)
Đúng 2
Bình luận (1)
Mọi người giải giúp mik với ạ, plss 🥺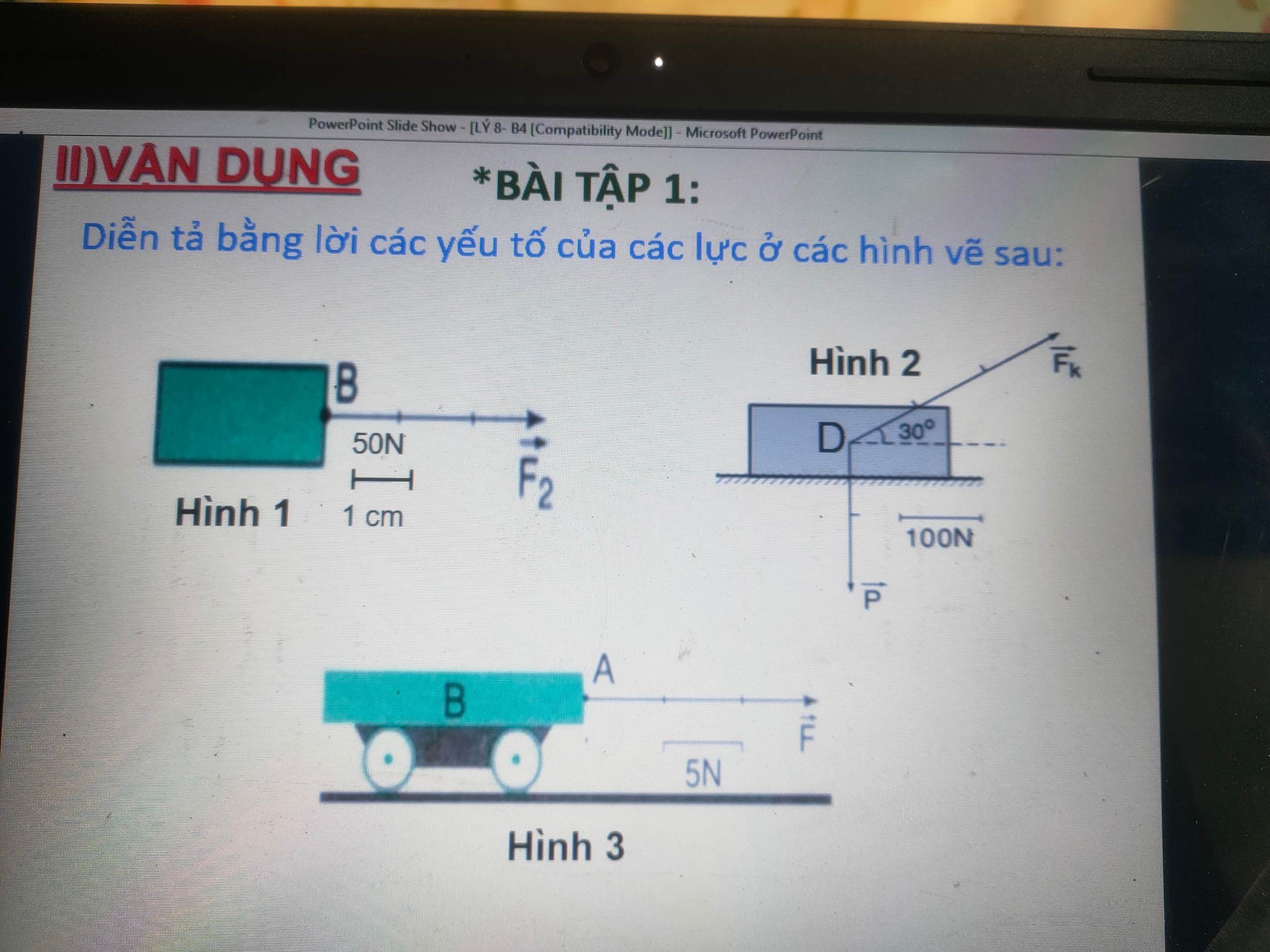
Mọi người giúp mik giải nha 🥺🥺🥺🥺🙏🏻🙏🏻🙏🏻🙏🏻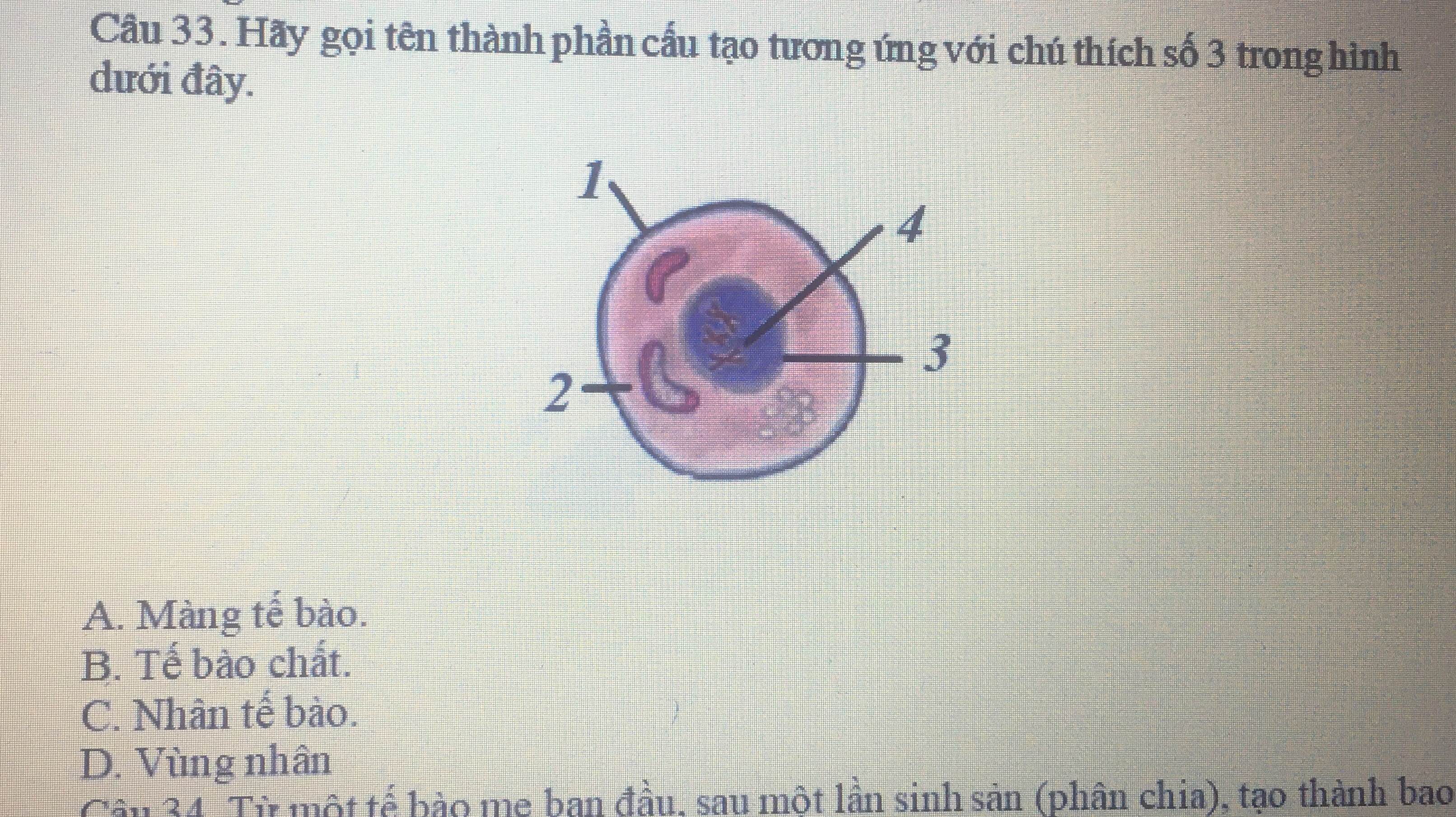
Xem thêm câu trả lời
Mọi người giải hộ mình câu 1, 2 với🥺
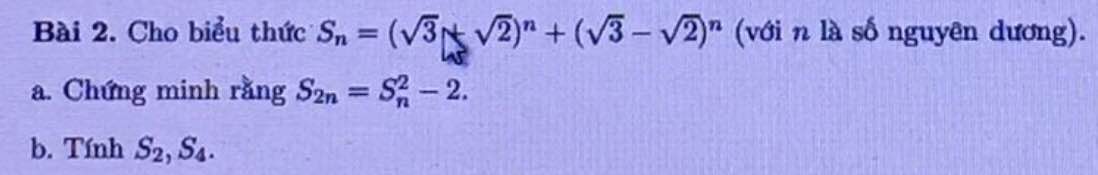 mọi người giải giúp em bài này với ạ 🥺
mọi người giải giúp em bài này với ạ 🥺
Các bạn ơi giúp mình với😰😥 mình không biết làm câu này thế nào ấy 😢mà mai mình nộp cho cô rồi 🥺🥺
Cách điều chế oxi trong phòng thí nghiệm
Giúp mình điii mọi người ơiii 🥺❤
Xem chi tiết
-Thí nghiệm: Cho một ít KMnO4 hoặc KClO3 vào ống nghiệm có cắm ống dẫn khí,đầu ống nghiệm được nút lại.
Đúng 0
Bình luận (0)
Câu hỏi là: cách điều chế oxi trong phòng thí nghiệm á
Giúp mình đi mọi ngừi ơiii 😥🥺
Đúng 0
Bình luận (0)
Trong phòng thí nghiệm, khí oxi được điều chế bằng cách đun nóng những hợp chất giàu oxi và dễ bị phân hủy ở nhiệt độ cao.
Đúng 1
Bình luận (0)
Xem thêm câu trả lời